Préliminaire

Supposons le problème suivant : un tableau a été volé il y a 10 ans dans une ville notée $C_1$. Le marché de l'art se concentre dans les capitales $C_1, C_2, C_3, C_4, C_5$, et la probabilité qu'un tableau passe d'une ville a une autre, au cours d'une période est connue :

Le graphe ci-dessus est à comprendre ainsi :

• il y a une probabilité de 0,88 pour qu'un tableau, situé dans la capitale $C_5$, se retrouve en $C_4$ au bout d'une période de 6 mois,
• il y a une probabilité de 0,25 pour qu'un tableau, situé dans la capitale $C_3$, se retrouve en $C_5$ au bout d'une période de 6 mois,
• etc.

ces probabilités étant estimées, par exemple, grâce à l'importance du marché de l'art entre ces différentes villes.

On voudrait savoir où ce tableau à le plus de chances de se trouver aujourd'hui, afin de mieux le rechercher.

Définitions

Les chaînes de Markov

Définition

Une chaîne de Markov est une suite de variables aléatoires $X_n$ à valeurs dans E (supposé ensemble d'entiers) telle que la probabilité conditionnelle de $X_{n+1}$ sur les états passés est fonction seulement de $X_n$ :

$P(X_{n+1} = j / X_0=i_0, X_1=i_1, ..., X_n=i_n) = P(X_{n+1} = j/X_n = i_n)$

En d'autres termes, la probabilité de passer à l'état $j$ au prochain coup d'horloge ne dépend pas de tout le parcours suivi ($i_0, i_1, ..., i_n)$ depuis le début des itérations, mais uniquement de l'état où l'on se trouve actuellement ($i_n$).

On peut interpréter cette définition en disant que c'est un processus à temps discret où le futur ne dépend que du présent, pas du passé.

Premier exemple

On considère trois enfants : Alice, Bob et Clara, qui jouent au ballon de la manière suivante...

• Quand Alice a le ballon, elle l'envoie une fois sur trois à Bob, et deux fois sur trois à Clara.
• Quand Bob a le ballon il l'envoie une fois sur deux à Alice, et une fois sur deux à Clara.
• Enfin, quand Clara a le ballon, elle l'envoie une fois sur quatre à Alice, et trois fois sur quatre à Bob.

On a bien affaire à une chaîne de Markov : ce processus n'a pas de mémoire. En d'autres termes, quand Clara a la balle, elle ne se soucie pas de savoir qui la lui a envoyé, pour décider à qui la renvoyer.

Un exemple type de problèmes qui nous intéresse ici peut être : sachant qu'Alice possédait la balle au départ, qui a le plus de chance de la posséder après dix itérations ?

Les chaînes de Markov homogènes

Définition : Une chaîne de Markov est dite homogène si la probabilité $P(X_{n+1} = j/X_n=i)$ est en outre indépendante de n.

De très nombreux processus stochastiques vérifient cette propriété. C'est le cas de nos enfants Alice, Bob et Clara : quand Alice a la balle, elle l'envoie une fois sur trois à Bob, et deux fois sur trois à Clara, et ce que ce soit à la première itération, à la cinquième ou à la $n$^ième.

Si, par contre, on avait considéré qu'Alice envoie la balle :

• à Bob avec une probabilité $\frac{1}{n}$,
• et à Clara avec une probabilité $\frac{n-1}{n}$,

où $n$ représente l'instant (le nombre d'itéLrations déjà écoulées), alors on n'aurait pas une chaîne homogène.

Travaux pratiques

Considérons un hamster ne pouvant réaliser que trois tâches rythmées par une unité de temps fixée (une minute par exemple) :

• Quand il dort, la probabilité de ne pas se réveiller la minute suivante est de 0,9.
• Quand il se réveille, la probabilité qu'il aille manger est de 0,5, la probabilité qu'il aille jouer sur sa roue est de 0,5.
• Quand il a mangé, la probabilité qu'il joue est de 0,3, celle qu'il dorme est de 0,7.
• Quand il joue, la probabilité qu'il retourne dormir est de 0,8. Sinon, il continue à jouer une minute de plus.

On demande de réfléchir aux questions suivantes :

1. A-t-on affaire à une chaîne de Markov ?
2. Si oui, est-elle homogème ?

Matrice de transition de la chaîne

Définition de la matrice de transition

Définition : Dans le cas des chaînes de Markov homogènes, on appelle probabilité de transition en une étape de l'état i à l'état j la valeur $p_{i,j} = P(X_{n+1}=j / X_n = i)$ indépendante de n, égale à la probabilité d'être au temps suivant en $j$ sachant qu'en ce moment on est en $i$.

Définition : Dans le cas d'un nombre fini d'états, la matrice $P = \left( \begin{array}{cccc} p_{1,1} & p_{1,2} & ... & p_{1,n} \\ p_{2,1} & p_{2,2} & ... & p_{2,n} \\ \vdots & & \ddots & \vdots \\ p_{n,1} & p_{n,2} & ... & p_{n,n} \end{array}\right)$ est dite matrice de transition de la chaîne.

Retour à Alice

Dans le cas de notre précédent exemple, la matrice de transition est $\left(\begin{array}{ccc} 0 & \frac{1}{3} & \frac{2}{3} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{4} & \frac{3}{4} & 0\end{array}\right)$

Notons qu'Alice aurait pu, par exemple, garder la balle une fois sur deux, et l'envoyer à Bob une fois sur 2 : les coefficients diagonaux ne sont pas forcément nuls dans une matrice de transition.

Matrices stochastiques

Puisque l'on a affaire à des probabilités (la première ligne, par exemple, contient les différentes probabilités d'envoi d'Alice), les coefficients de cette matrice de transition sont donc dans [0,1], et toutes les lignes sont de somme 1 : on parle de matrice stochastique.

Définition : Une matrice stochastique est une matrice dont tous les coefficients sont dans [0,1], et dont la somme par ligne est égale à 1.

Ces matrices stochastiques ont les propriétés suivantes :

  Théorème : 
  * Toute matrice stochastique P admet le vecteur colonne C dont

  $\left( \begin{array}{cccc} p_{1,1} & p_{1,2} & ... & p_{1,n} \\ p_{2,1} & p_{2,2} & ... & p_{2,n} \\ \vdots & & \ddots & \vdots \\ p_{n,1} & p_{n,2} & ... & p_{n,n} \end{array}\right) \times \left( \begin{array}{c}1 \\ 1 \\ \vdots \\ 1 \end{array}\right) = 1 \times \left( \begin{array}{c}1 \\ 1 \\ \vdots \\ 1 \end{array}\right)$

  * Réciproquement, si une matrice P à coefficients positifs, est

  * Si P est une matrice stochastique, alors ses puissances le

  * Toute valeur propre $\lambda$ d'une matrice stochastique vérifie $|\lambda|\leqslant 1$.

Ce résultat provient du fait que la somme par ligne d'une telle matrice redonne toujours 1. Notons qu'à une matrice stochastique et à un état initial, on peut associer une chaîne de Markov, et réciproquement.

Travaux pratiques

1. Dresser la matrice de transition de la chaîne de Markov associée au hamster.
2. Vérifier que les matrices de transitions associées à Alice et au Hamster sont bien stochastiques.
3. Retrouver, dans ces cas particuliers, les propriétés énoncées ci-dessus.

Transition en m étapes

Résultats

  Théorème : 
  La probabilité de passage de i à j en m étapes est égale à l'élément

La démonstration de ce résultat se fait par récurrence sur m, en appliquant la formule des probabilités totales.

Exemple

Par exemple, dans le cas de notre jeu de balle,

  >>> from sympy import *
  >>> M = Matrix((0,Rational(1,3),Rational(2,3),\
                 Rational(1,2),0,Rational(1,2),\
                 Rational(1,4),Rational(3,4),0)).reshape(3,3)
  >>> M
  [  0, 1/3, 2/3]
  [1/2,   0, 1/2]
  [1/4, 3/4,   0]
  >>> M**2
  [1/3,   1/2,   1/6]
  [1/8, 13/24,   1/3]
  [3/8,  1/12, 13/24]

Donc, il y a :

• une chance sur deux que la balle passe des mains de Alice dans ceux de Bob en deux étapes, puisque $M_{1,2}^2 = \frac{1}{2}$,
• 13 chances sur 24 que la balle revienne à Bob deux étapes après qu'il ait envoyé la balle à quelqu'un,
• etc.

De même,

  >>> M**3
  [ 7/24, 17/72, 17/36]
  [17/48,  7/24, 17/48]
  [17/96, 17/32,  7/24]

Donc, il y a 7 chances sur 24 pour qu'Alice reçoive la balle trois étapes après l'avoir envoyée.

Période, état apériodique

Définition : La période d d'un état i d'une chaîne de Markov est égale au plus grand diviseur commun de tous les n tels que $p_{ii}^(n)>0$.

Définition : Si d>1, alors l'état i est périodique. Sinon, il est apériodique.

Travaux pratiques

1. Faire une fonction qui teste si une matrice passée en argument est stochastique, ou ne l'est pas.
2. Vérifier, sur des exemples, que la matrice de transition d'une chaîne de Markov possède bien toujours le vecteur propre $(1,1, ..., 1)^T$ associé à la valeur propre 1.
3. Déterminez la probabilité que la balle passe :
   • de Alice à Bob en 3 étapes,
   • de Bob à Clara en 7 étapes,
   • de Clara à Alice en 40 étapes.
4. Procédez pareillement avec le hamster.

Pour la représentation matricielle de la chaîne de Markov, on pourra utiliser, au choix : sympy ou numpy.

Graphe de transition

Présentation

On peut associer à une chaîne homogène son graphe de transition : les sommets du graphe pondéré sont les états, et on dessine une flèche entre les états i et j si $p_{i,j}>0$, le poids associé étant $p_{i,j}$.

Beaucoup d'informations peuvent se déduire de l'examen du graphe de transition. On pourra, par exemple, voir si un état x est accessible à partir d'un état y par l'existence d'un chemin entre x et y.

Exemple

On peut représenter la matrice de transition

$\left( \begin{array}{ccc} \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ 0 & \frac{1}{2} & \frac{1}{2} \end{array} \right)$

par le graphe de transition...

Représentation

Il existe un langage, du nom de dot, permettant de décrire les graphes afin de les représenter.

Par exemple, pour réaliser le graphe ci-dessus, j'ai saisi ce qui suit dans un fichier toto.dot...

  strict digraph  {
	1 -> 1 [label = "1/2"];
	1 -> 2 [label = "1/2"];
	2 -> 1 [label = "1/3"];
	2 -> 2 [label = "1/3"];
        2 -> 3 [label = "1/3"];
	3 -> 2 [label = "1/2"];
	3 -> 3 [label = "1/3"];
  }

et, dans un shell, j'ai transformé ce fichier texte en image :

  $ dot toto.dot -T png > toto.png

L'option -T permet de spécifier le type de fichier de sortie. Pour visualiser ledit fichier :

  $ eog toto.png

Travaux pratiques

• Faire une fonction qui crée le fichier .dot à partir de la matrice de transition. On rappelle que pour ouvrir un fichier en mode écriture, écrire quelque chose et fermer ledit fichier, il faut procéder ainsi...

 >>> unFichier = open('nomFichier.dot','w')
 >>> unFichier.write('quelque chose')
 >>> unFichier.close()

• Faire une fonction qui visualise le graphe. On pourra avoir recours à la fonction system, pour exécuter une commande shell...

 >>> from os import system
 >>> system('firefox')

• Représenter les graphes associés au hamster et à Alice.

NB : Les bibliothèques nécessaires à dot, à savoir graphviz, ne sont peut-être pas installées en salle de TP. Dans ce cas, faites toujours le fichier .dot et la fonction de visualisation : elles marcheront chez vous...

Le modèle de diffusion d'Ehrenfest

Présentation de l'exemple

Ce modèle a été introduit en 1907 et peut décrire la diffusion d'un gaz placé dans deux récipients à température différente mis en communication. Il nous servira d'exemple, comme Alice et sa balle, pour comprendre le principe des chaînes de Markov.

On considère deux urnes A et B contenant au total a boules. A chaque étape, on tire une des boules avec la probabilité $\frac{1}{a}$, et on la change d'urne. On représente l'état du système par $X_n$ : nombre de boules dans l'urne A au temps n.

Ce processus est une chaîne de Markov homogène de matrice de transition de dimension a+1. Par exemple, pour a=4, on obtient

$ \left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 1/4 & 0 & 3/4 & 0 & 0 \\ 0 & 1/2 & 0 & 1/2 & 0 \\ 0 & 0 & 3/4 & 0 & 1/4\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}\right] $

Travaux pratiques

1. Créez, pour un nombre $a$ de boules totales données, la matrice de transition associée pour le modèle d'Ehrenfest.
2. Faire une fonction qui, à $X_0$ et $n$ donné, renvoie $X_n$.
3. Représentez le graphe d'Ehrenfest.

Classification

Relation d'équivalence

Définitions

Définition : Nous dirons que l'état j est accessible depuis l'état i quand il existe au moins un chemin de probabilité non nulle menant de i à j : $\exists n \in \mathbb{N}, p_{ij}^(n)>0$.

Définition : Nous dirons que les états i et j communiquent quand l'état j est accessible depuis l'état i et quand l'état i est accessible depuis l'état j.

Théorème

  Théorème : 
  La relation communiquer est une relation d'équivalence.

On définit alors les classes d'équivalence formées de tous les éléments qui communiquent entre eux : c'est l'opération de classification.

Graphe réduit

Soit

$P = \left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ \frac{2}{3} & 0 & \frac{1}{3} & 0 & 0 \\ 0 & \frac{1}{2} & 0 & \frac{1}{6} & \frac{1}{3} \\ 0 & 0 & 0 & 1 & 0 \\ 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} \end{array}\right)$

qui donne le graphe

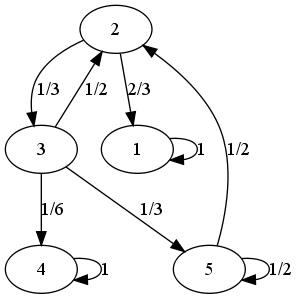
La classification donne ici trois classes :

• $C_1 = \{ 1 \}$,
• $C_2 = \{ 2, 3, 5 \}$,
• $C_3 = \{ 4 \}$.

À partir de là, on peut écrire le graphe réduit, dont les sommets sont les classes et pour lequel un arc, par exemple de $C_u$ vers $C_v$, signifie qu'il existe $i \in C_u$ et $j \in C_v$ tel que $p_{ij}>0$.

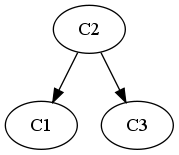
Exemple

On peut facilement faire apparaître les classes d'équivalence en regardant le graphe de transition. Par exemple, le graphe suivant :

Se réduit en :

Dans cet exemple, on voit que :

• si l'état initial était 1, on va rester dans cet état,
• si l'état initial était 2 ou 4, on va rester perpétuellement entre les états 2 ou 4 : ce sont des classes d'états finales.
• Les états 3,5 et 6 sont d'une autre nature : on n'y restera qu'un temps fini avant d'évoluer vers l'une ou l'autre des classes finales (et y rester).

Travaux pratiques

1. Tracer le graphe réduit du modèle d'Ehrenfest, pour plusieurs valeurs de $n$. Faire de même pour l'exemple d'Alice.
2. Les représenter
3. Faire une fonction retournant les classes d'équivalences associées à une chaîne de Markov donnée sous forme d'une matrice.
4. Faire une fonction traçant le graphe réduit d'une chaîne de Markov, en exploitant la fonction précédente.

Types de classes

Il existe plusieurs types de classes, et de chaînes : les reconnaître permet de les classifier...

Définitions : Une classe est transitoire si on peut en sortir. Sinon, elle est persistante. Une classe persistante constituée d'un seul élément est absorbante.

Définitions : Une chaîne est irréductible si elle ne comporte qu'une seule classe. Elle est absorbante si toutes ses classes persistantes sont absorbantes.

Travaux pratiques

1. Relevez, dans les trois exemples de ce texte (Ehrenfest, Hamster et Alice), les différents types de classes, de chaînes.
2. Faire de même avec l'exemple préliminaire (le vol de tableau).

Comportement transitoire

Préliminaires

Distribution de probabilité

Soit $p_i^(n) = P(X_n = i)$. On regroupe toutes les probabilités dans un vecteur ligne appelé distribution après $n$ transitions :

$\pi^(n) = \left(p_1^(n), p_2^(n), ..., p_r^(n)\right)$

Les éléments de ce vecteur sont des probabilités, donc comprises entre 0 et 1, telles que la somme vaut 1. On remarque de plus que :

• $\pi^(0)$ est la distribution initiale,
• $\pi^(1) = \pi^(0) P$,
• $\pi^(2) = \pi^(1) P = \pi^(0) P^2$,
• etc.

On en déduit donc que

$\pi^(n+1) = \pi^(0) P^{n+1} = \pi^(n) P$

Exemple

Revenons à notre jeu de balle, et supposons que l'on soit sûr qu'Alice aura la balle au début du jeu : la distribution $\pi^(0)$ est donc $(1,0,0)$. Calculons la distribution après une itération :

  >>> M
  [  0, 1/3, 2/3]
  [1/2,   0, 1/2]
  [1/4, 3/4,   0]
  >>> V = Matrix((1,0,0)).reshape(1,3)
  >>> V
  [1, 0, 0]
  >>> V=V*M
  >>> V
  [0, 1/3, 2/3]

Ainsi donc, après une itération,

• Alice n'a aucune chance d'avoir la balle,
• Bob a une chance sur trois d'avoir la balle,
• Clara a deux chances sur 3.

Poursuivons...

  >>> V=V*M
  >>> V
  [1/3, 1/2, 1/6]

Ainsi, à la deuxième itération, la balle a :

• une chance sur trois d'être dans les mains d'Alice,
• une chance sur deux de l'être dans ceux de Bob,
• une chance sur six, enfin, de l'être dans ceux de Clara.

On peut continuer ainsi, pour prévoir le futur proche, la distribution des probabilités :

  >>> V=V*M
  >>> V
  [7/24, 17/72, 17/36]
  >>> V=V*M
  >>> V
  [17/72, 65/144, 5/16]
  >>> V=V*M
  >>> V
  [175/576, 541/1728, 331/864]

La collection des $\pi^(n)$ représente donc le comportement transitoire de la chaîne de Markov, qui est ainsi pleinement déterminé. Reste à savoir ce qui se passe à terme...

Travaux pratiques

1. Regardez comment évolue la distribution de probabilité quand Bob a la balle au départ, et quand c'est Clara qui l'a.
2. Regardez, de même, l'évolution des distributions de probabilités pour les modèles du Hamster et de Ehrenfest.

Nombre de passages

État récurrent

Revenons à l'étude du cas plus général d'une chaîne homogène, et intéressons-nous à la variable aléatoire $N_x$ qui compte le nombre de passages de la chaîne dans l'état x.

Supposons que la chaîne parte de l'état x, et soit q la probabilité de revenir à l'état x en temps fini. Puisque l'on part de x, on a $N_x > 0$.

Ce processus stochastique n'ayant aucune mémoire du passé, la probabilité de l'événement $N_x = 2$ correspond au produit de q (de x, je reviens en x) par 1-q (de x, je ne reviens jamais en x). De la même façon :

$ P(N_x = k) = q^{k-1} (1-q)$

Définition : Nous dirons qu'un état x est récurrent si la probabilité de revenir en x en un temps fini est égale à 1.

Résultat

Remarquons pour commencer que toute chaîne de Markov finie possède un état récurrent, car on a un nombre infini de pas, et un nombre fini d'états : il existe au moins un état que l'on va visiter une infinité de fois.

De plus, le fait d'être récurrent est compatible avec la relation d'équivalence vu plus haut : si x et y sont dans la même classe d'équivalence, et si x est récurrent, alors y l'est aussi.

On peut montrer une propriété plus forte :

Donc, quand on est dans une classe récurrente, on ne peut plus en sortir : c'est la même notion que celle de classe finale.

Définition : Les états non récurrents sont dits transitoires.

C'est également une propriété commune aux états d'une même classe.

Travaux pratiques

Recherchez les états transitoires, et récurrents, pour les trois exemples.

Comportement asymptotique

Distribution stationnaire

Présentation du problème

On veut connaître la loi de distribution $\pi^(n)$ quand n tend vers l'infini.

En particulier, on veut savoir :

• y a-t-il convergence ?
• dépend-t-elle de la distribution initiale ?
• pour un état persistant, quel va être le temps moyen de séjour dans cet état ?
• pour un état transitoire, quel est le nombre de visites à cet état ?

Un premier cas de figure vient immédiatement à l'esprit : celui où la chaîne de Markov n'évolue plus à partir d'un certain temps, reste stationnaire.

Distribution stationnaire

Définition : Une distribution $\pi$ est dite stationnaire si $\pi P = \pi$. La chaîne $X_n$ associée à P et commençant au temps 0 par la distribution $\pi$ est donc invariante.

Par exemple, pour

$\left( \begin{array}{ccc} \frac{1}{2} & \frac{1}{2} & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array} \right)$

la distribution $\pi = \left(\frac{1}{2} , \frac{1}{4}, \frac{1}{4} \right)$ est invariante.

Vers une distribution limite

On peut déjà remarquer que si la distribution limite existe, alors elle est stationnaire. On a, de plus, les résultats suivants (admis)...

  Théorème : 
  Toute chaîne de Markov finie possède toujours au moins une  distri-
  bution invariante.

  Théorème : 
  Pour une chaîne de Markov finie, les deux valeurs suivantes sont
  égales :
    - le nombre de distributions invariantes linéairement
        indépendantes
    - l'ordre de multiplicité de la valeur propre 1 de sa matrice de
        transition.
  De plus, cette multiplicité est égale au nombre des classes
  persistantes de la chaîne.

Exemple

Soit la matrice stochastique $P = \left( \begin{array}{cccc} \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 1 & 0 \end{array}\right)$

Son polynôme caractéristique vaut $\Phi(\lambda) = \left(\lambda - \frac{1}{4} \right) \left( \lambda - 1 \right)^2 \left( \lambda + \frac{1}{2} \right)$ On aura donc deux lois stationnaires indépendantes.

Cherchons les distributions stationnaires ($\pi = \pi P$). On obtient 4 équations à 4 inconnues, auquel il faut ajouter la condition : "la somme des éléments de $\pi$ est égale à 1".

On trouve, par exemple : $\pi_1 = (0,1,0,0)$ et $\pi_2 = \left(0,0,\frac{2}{3},\frac{1}{3}\right)$, et tout barycentre de ces vecteurs est une distribution stationnaire.

Travaux pratiques

Déterminez, pour chacun des trois exemples du texte :

• le nombre n de distributions invariantes,
• n distributions linéairement indépendantes.

On pourra procéder comme ci-dessus, et utiliser pleinement les fonctions développées dans le TP sur les valeurs propres , ou les fonctions prédéfinies dans sympy et numpy (en particulier, pour la résolution du système linéaire).

Distribution limite

Présentation du problème

On a vu, avec Alice, que la distribution des probabilités $\pi^(n)$ évoluait au cours du temps. Il est intéressant de savoir si cette évolution admet une limite, pour $n \rightarrow +\infty$.

Si, par exemple, la distribution limite dans le cas du jeu de balle est $(1,0,0)$, on sait qu'à la fin de la journée il suffira de trouver Alice pour trouver la balle...

Unicité de la distribution limite

Commençons par nous intéresser au nombre de limites possibles...

  Théorème : 
  Si la distribution limite $\lim_{n \rightarrow +\infty} \pi^(n)$ :
       - existe,
       - est indépendante de la distribution initiale $\pi^(0)$,
  alors la chaîne possède une seule classe persistante.

  De plus, $\lim_{n \rightarrow +\infty} \pi^(n)$ existe et est indépendante de $\pi^(0)$ si
  et seulement si :
       - $\lim_{n \rightarrow +\infty} P^{n}$ existe,
       - et cette limite est égale à une matrice de transition $P^*$ dont
         toutes les lignes sont égales entre elles.

  Une ligne de $P^*$ est alors la distribution limite.

On voit donc l'intérêt d'être capable de calculer la limite de la suite de puissances matricielles $P^n$...

Travaux pratiques

Reprenez chacun des trois exemples du texte, et déterminez (grâce au calcul de la limite de $P^n$, où $P$ est la matrice de transition respective) s'il y a existence d'une distribution limite, et indépendance par rapport à la distribution initiale.

On pourra, une fois encore, utiliser le TP d'algèbre linéaire sur les valeurs propres et vecteurs propres, s'il a été fait, pour calculer la limite de $P^n$, et sinon s'en remettre à numpy et sympy.

Déterminez, le cas échéant, cette distribution limite. Que peut-on en conclure concrètement ?

Existence de la distribution limite

  Théorème : 
  Soit $P$ la matrice de transition d'une chaîne irréductible et apério-
  dique (tous les états sont apériodiques). Les propriétés suivantes 
  sont vérifiées :
     - Pour toute distribution initiale $\pi^(0)$, on a
                $\lim_{n \rightarrow +\infty} \pi^(n) = \lim_{n \rightarrow +\infty} \pi^(0) P^n = \pi^*$,
     - $\pi^*$ est l'unique solution du système $\pi = \pi P$ et $\pi_1+...+\pi_n = 1$.
     - $\forall i, \mu_i = \frac{1}{\pi_i^*}$ est égal au nombre moyen de transitions entre deux
       visites successives à l'état $i$. 

Travaux pratiques

Appliquez ce résultat à chaque exemple du texte.

Cas des chaînes réductibles

On suppose que l'on a plusieurs classes. On a :

• des classes persistantes (ou absorbantes),
• des classes transitoires.

  Pour tout état initial $i$, la probabilité d'être dans un état per-
  sistant à l'étape $n$ tend vers 1 quand $n$ tend vers l'infini
  De la même façon, la probabilité d'être dans un état transitoire
  tend vers 0.

Forme Canonique de P

Présentation

On donne une forme canonique à P en renumérotant les états :

• on place les états des classes persistantes en premier,
• puis, les états transitoires.

P a alors la forme canonique suivante :

$P = \left( \begin{array}{ccccc} P_1 & 0 & ... & 0 & 0 \\ 0 & P_2 & 0 & ... & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & ... & 0 & P_k & 0 \\ R_1 & R_2 & ... & R_k & Q \end{array} \right)$

Chaque $P_i$ est une chaîne de Markov irréductible sur la classe persistante $C_i$ (les $P_i, R_i$ et $Q$ ci-dessus sont donc des matrices).

Cas d'une chaîne absorbante

Si la chaîne de Markov est absorbante, la forme canonique de P sera :

$P = \left( \begin{array}{cc} I & 0 \\ R & Q \end{array} \right)$

Si on calcule $P^2$, ou plus généralement $P^n$, on obtient :

$P^2 = \left( \begin{array}{cc} I & 0 \\ R + QR & Q^2 \end{array} \right) \textrm{ et } P^n = \left( \begin{array}{cc} I & 0 \\ \sum_{i=0}^{n-1}Q^i R & Q^n \end{array} \right) $

donc

$\lim_{n \rightarrow +\infty} P^n = \left( \begin{array}{cc} I & 0 \\ (I-Q)^{-1} & 0 \end{array} \right)$

Définition : On note $N = (I-Q)^{-1}$ la matrice fondamentale de la chaîne de Markov.

Le résultat précédent permet de calculer $\pi^*$...

  Soit une chaîne de Markov débutant de l'état transitoire $i$.
  Le nombre moyen de périodes passées dans un état transitoire $j$ est
  égal à l'élément $n_{ij}$ de la matrice $N$.
  De plus, partant d'un état transitoire $i$, le nombre moyen de transi-
  tions avant d'atteindre un état absorbant est égal à la somme des
  éléments de la ligne $i$ de $N$.

Travaux pratiques

Appliquez ce résultat à chaque exemple du texte.

Chaînes ergodiques et régulières

Définitions

Définition : Une chaîne de Markov finie est dite ergodique (ou irréductible) si tout état est atteignable en un nombre fini d'étapes à partir de tout autre état.

On peut demander une propriété plus forte, le fait qu'il existe un nombre d'étapes qui permet de passer de tout état à tout autre état.

Définition : Nous dirons donc qu'une chaîne est régulière s'il existe un m tel que tous les coefficients de $P^m$ sont strictement positifs.

Ceci se traduit sur le graphe de transition par l'existence pour tout couple d'états $(x,y)$, d'un chemin entre $x$ et $y$ de longueur m.

Cas des chaînes régulières

Dans le cas d'une chaîne régulière, on peut généraliser la théorie précédente, et l'on obtient :

Ce théorème est puissant, puisqu'il permet de prouver l'existence d'une distribution limite, et de la prouver sans avoir à calculer la matrice $P^m$.

Le cas des chaînes ergodiques

Pour une chaîne ergodique, on n'a pas forcément l'existence d'une limite pour $P^n$. Par contre, il existe une unique distribution $\pi$ telle que $\pi P = \pi $.

Comment interpréter cette distribution stationnaire de P ?

Une étude approfondie permet de montrer que la proportion de temps passé dans l'état i pendant les n premières étapes admet pour limite $\pi_i$ (quand n tend vers $\infty$).

Cette proportion est donc indépendante de l'état de départ.

Le temps de premier retour

Considérons maintenant une chaîne ergodique partant de l'état $X_0 = i $. On va revenir à cet état, par ergodicité.

Définition : La variable aléatoire $t_i = inf \{ k>0 / X_k = i \} $ est dite temps de premier retour en i. Son espérance $\tau_i$ est dite temps de récurrence moyen en i.

On peut prouver que...

Exemple complet

Présentation

Les études de licence durent trois ans. À l'issue de chaque année, chaque élève a :

• une probabilité $p$ de passer dans l'année supérieure (ou d'obtenir son diplôme, s'il est en troisième année),
• une probabilité $q$ de redoubler,
• une probabilité $r$ d'être renvoyé.

Le cursus d'un élève peut être modélisé par une chaîne de Markov à cinq états, dont deux sont absorbants R et D (qui correspondent respectivement à être renvoyé et diplômé) :

Probabilité d'obtention du diplôme

L'évaluation de la probabilité $a_{iD}$ qu'un élève obtienne un jour son diplôme, étant pour l'instant dans l'état $i$, peut être obtenue en décomposant l'événement

{ partant de l'état $i$, le système va être absorbé par $D$ }

selon l'issue de la première transition, et en utilisant le caractère sans mémoire de l'évolution du système. Il vient :

$\left\{\begin{array}{lll} a_{1D} & = & q a_{1D} + p a_{2D} + r a_{RD} \\ a_{2D} & = & q a_{2D} + p a_{3D} + r a_{RD} \\ a_{3D} & = & q a_{3D} + p a_{DD} + r a_{RD} \end{array}\right.$

Mais nous avons $a_{RD} = 0, a_{DD} = 1$ et $p+q+r = 1$, d'où le nouveau système linéaire à résoudre :

$\left\{\begin{array}{rll} (p+r) a_{1D} - p a_{2D} & = & 0 \\ (p+q) a_{2D} - p a_{3D} & = & 0 \\ (p+r) a_{3D} & = & 0 \end{array}\right.$

Dont la solution est :

$a_{3D} = \frac{p}{p+r} ~ ~ ~ a_{2D} = \left(\frac{p}{p+r}\right)^2 ~ ~ ~ a_{1D} = \left(\frac{p}{p+r}\right)^3$

Pour tout état $i$, nous avons $a_{iD}+a_{iR} = 1$ (tout élève finira soit par être renvoyé, soit par obtenir son diplôme) : on peut alors en déduire les valeurs de $a_{1R}, a_{2R}$ et $a_{3R}$.

Durée moyenne des études

La fin des études est associée aux états $R$ ou $D$. Ces deux états peuvent être regroupés en un état $F$ et nous considérons la chaîne ci-dessous à quatre états, dont seul l'état $F$ est absorbant avec $p_{3F} = p+r$.

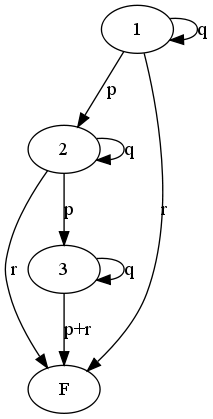
Appelons $\overline{t_i}$, pour $i=1,2,3$, le temps moyen de séjour dans les états transitoires $(1,2,3)$ avant absorption par $F$ (la durée moyenne des études est alors $\overline{t_1}$ ; en considérant le résultat de la première transition et en utilisant le caractère sans mémoire de la chaîne (le temps moyen d'absorption à partir de l'état $i$ ne dépend que de $i$), nous pouvons écrire

$\overline{t_1} = r 1 + q(1+\overline{t_1}) + p (1+\overline{t_2})$

c'est-à-dire :

$\overline{t_1} = 1 + q\overline{t_1} + p\overline{t_2}$

De même

$\overline{t_2} = 1 + q\overline{t_2} + p\overline{t_3} \textrm{ et } \overline{t_3} = 1 + q\overline{t_3}$

La solution de ce système est :

$ \overline{t_3} = \frac{1}{1-q}, ~ ~ ~ \overline{t_2} = \frac{2p+r}{(1-q)^2} = \frac{2p+r}{(p+r)^2}, ~ ~ ~ \overline{t_1} = \frac{3p^2+3rp + r^2}{(p+r)^3}$

Durée moyenne d'obtention d'un diplôme

Élèves diplômés

Il faudra s'intéresser aux seules trajectoires qui se terminent par $D$, c'est-à-dire que l'on s'intéresse au cursus d'un étudiant dont on sait qu'il obtiendra son diplôme.

Les probabilités de transition $p_{ij}$ doivent alors être remplacées par les probabilités de passage de $i$ à $j$ conditionnées par une absorption par l'état $D$. En appliquant la définition des probabilités conditionnelles, nous avons :

$ P \left(\textrm{passage de } i \textrm{ à } j | \textrm{absorption par } D\right) = \frac{P \left(\textrm{passage de } i \textrm{ à } j \textrm{ et absorption par } D\right)}{P \left(\textrm{absorption par } D\right)}$

qui est égal à $p_{ij} \frac{a_{jD}}{a_{iD}}$.

Pour les élèves heureux, la chaîne est alors la suivante :

Il est alors simple de calculer, par la même méthode que ci-dessus, le temps moyen d'absorption par $D$. On trouve :

$ \overline{t_1^D} = \frac{3}{p+r}, ~ ~ ~ \overline{t_2^D} = \frac{2}{p+r}, ~ ~ ~ \overline{t_3^D} = \frac{1}{p+r}$

Élèves renvoyés

Considérons désormais les cursus des élèves renvoyés. Pour eux, les probabilités de passage doivent être conditionnées par l'absorption par l'état $R$, $p_{ij}$ devient $p_{ij} \frac{a_{jR}}{a_{iR}}$.

La chaîne associée est alors la suivante :

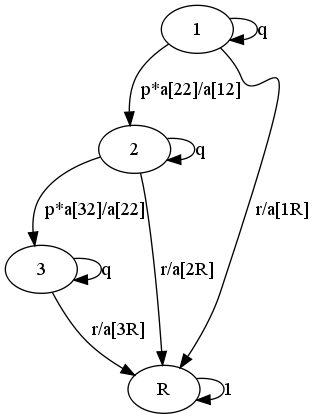
Le calcul des temps d'absorption par l'état $R$ donne, en employant la même méthode que ci-dessus :

$ \overline{t_3^R} = \frac{1}{p+r}, ~ ~ ~ \overline{t_2^R} = \frac{1}{p+r}\times \frac{r+3p}{r+2p}, ~ ~ ~ \overline{t_1^R} = \frac{1}{p+r}\times\frac{6p^2+r^2+4pr}{r^2+3p^2+3rp}$

Il est alors facile de vérifier que le temps moyen de fin d'études $\overline{t_1}$ doit satisfaire la relation :

$\overline{t_1} = \overline{t_1^D}a_{1D} + \overline{t_1^R} a_{1R}$

Travaux pratiques

Faire le même travail avec le master, qui se déroule normalement sur deux ans.

On résoudra les systèmes obtenus par un pivot de Gauss, si le TP du même nom a été fait, ou par une fonction solve de numpy ou sympy sinon.

On représentera les chaînes de Markov intermédiaires, avec les fonctions définies précédemment.