La droite

Rappels

On souhaite tracer la courbe représentative de la fonction $f(x) = ax + b$. En effet, l'équation d'une droite non verticale est de la forme $y = ax+b$, par exemple $y = 2x+3$, où

• $a$ est la pente de la droite. $a = 2$ peut être compris ainsi : on monte deux fois plus vite que l'on avance.
• $b$ est l'ordonnée à l'origine : $y = b$ quand $x = 0$.

Premier tracé

Dans le cas d'une droite (non verticale), $y = f(x)$, où $f(x) = ax+b$ ($a$ et $b$ étant des paramètres connus).

On a donc affaire à une fonction : à chaque $x$ correspond un unique $y$, donné par la formule $y = ax+b$.

L'idée de base, pour représenter un tel objet, consiste à parcourir l'ensemble des $x$ de notre image, et pour chacun de ces $x$ :

1. calculer le $y = ax+b$ associé,
2. afficher $(x,y)$.

Ainsi donc, si notre image a une taille $512 \times 512$, et que l'on souhaite tracer la droite $y = 2x+3$, l'algorithme suivant conviendra :

  pour x de 1 à 512 faire
      y = 2*x+3
      afficher (x,y)

Précaution d'emploi

Un tel algorithme est à adapter à la bibliothèque graphique que vous utilisez.

Ainsi, avec PIL sous python, le pixel (0,0) est le pixel supérieur gauche de l'image, ce qui signifie que l'axe des ordonnées est orienté vers le bas :

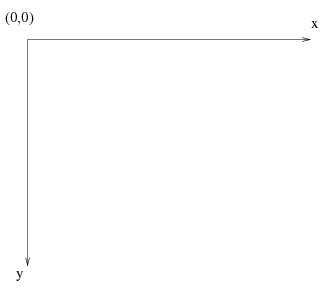
Si donc on veut tracer une droite allant du coin inférieur gauche au coin supérieur droit, comme suit :

il faudra bien faire attention à l'équation de droite recherchée :

• quand on avance d'un pixel en $x$, on doit diminuer l'ordonnée de 1, d'où une pente $a = -1$,
• pour $x = 0$, on affiche le pixel tout en bas, de coordonnées $(0;255)$, donc $b = 255$.

D'où la droite à afficher : $y = -x + 255$

Cette précaution d'emploi est à prendre dans tout ce qui suit : les équations mathématiques doivent toujours être adaptées aux repères géométriques choisis par la bibliothèque graphique retenue.

Code python

D'où le code python recherché pour l'affichage de notre droite :

  import Image as im
  mon_image = im.new('1',(256,256))
  def f(x):
    return -x + 255
  for x in range(256):
    mon_image.putpixel((x,f(x)),255)

  mon_image.show(command = 'eog')

Ce code est assez "bas niveau" : la technique marchera à partir du moment où on peut

• ouvrir une image,
• afficher un pixel en position $(x,y)$, dans une couleur choisie.

Cette méthode pourra donc être appliquée quelle que soit la bibliothèque graphique choisie.

Autre méthode

On peut aussi avoir sous la main un plotteur, c'est-à-dire une fonction recevant deux vecteurs $X$ et $Y$ de même taille $N$, et affichant les $N$ pixels de coordonnées $(x,y)$, où $x$ décrit $X$ et $y$ décrit $Y$.

Alors, avec ce plotteur, on peut facilement tracer tous les objets se mettant sous la forme $y = f(x)$, c'est-à-dire toutes les courbes de fonctions mathématiques : polynômes, logarithmes et exponentielles, sinusoïdes, etc.

Pour cela, il suffit de prendre :

• pour $X$ l'ensemble des abscisses possibles pour les pixels,
• pour $Y$ l'ensemble des $f(x)$, où $x$ décrit $X$.

Sous python, un plotteur peut se trouver dans le module pylab. Pour tracer $y = f(x)$ dans une image $512 \times 512$, on pourra procéder ainsi :

  import pylab as P
  def f(x):
    return -x + 255

  X = range(256)
  Y = [f(x) for x in X]
  P.plot(X,Y)
  P.show()

Dans ce qui précède, la fonction $f$ est à adapter à vos besoins.

On remarquera pour finir que la convention des axes de pylab n'est pas celle de PIL : ces derniers supposent que l'axe des $Y$ est orienté vers le haut. Aussi, pour obtenir le même dessin que précédemment, il faudrait utiliser la fonction $f(x) = x$.

Travaux pratiques

• Réalisez l'image suivante :

• Réalisez l'image suivante :

• Réalisez l'image suivante :

Le cercle

Rappels

Un cercle de centre $(a,b)$ et de rayon $R$ a pour équation $(x-a)^2 + (y-b)^2 = R^2$

Ainsi, l'équation d'un cercle de centre $(0,0)$, rayon 2, est $x^2 + y^2 = 4$.

Le tracé

On peut adopter les méthodes précédentes au tracé d'un cercle.

Pour la première méthode, il faudrait connaître le(s) $y$ associés à chaque $x$ de l'image. Cela peut s'obtenir en réécrivant légèrement l'équation algébrique du cercle :

$(x-a)^2 = R^2 - (y-b)^2$ donc $y-b = \pm \sqrt{R^2 - (x-a)^2}$ soit $y = b \pm \sqrt{R^2 - (x-a)^2}$

En remarquant que, pour un $x$ donné,

• si $R^2 < (x-a)^2$, alors la racine n'a pas de sens (dans les réels), et il n'y a pas de point du cercle à cet abscisse $x$.
• si $R^2 = (x-a)^2$, il y a un seul $y (=b)$ associé au $x ( = a \pm R)$.
• sinon, on trouve bien deux $y$ pour un $x$.

Tout cela est normal : une droite verticale peut couper un cercle en 0, 1 ou 2 points !

Un premier algorithme pour tracer le cercle de centre $(a,b)$, rayon $R$, pourrait donc être :

      Si $R^2 \geqslant (x-a)^2$,
          $y_0 = \sqrt{R^2 - (x-a)^2}$
          afficher $(x, b-y_0)$
          afficher $(x, b+y_0)$

Travaux pratiques

• Tracer ce bout de cercle :

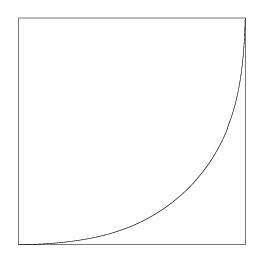
• Tracer ce cercle :

• Tracer cette figure :

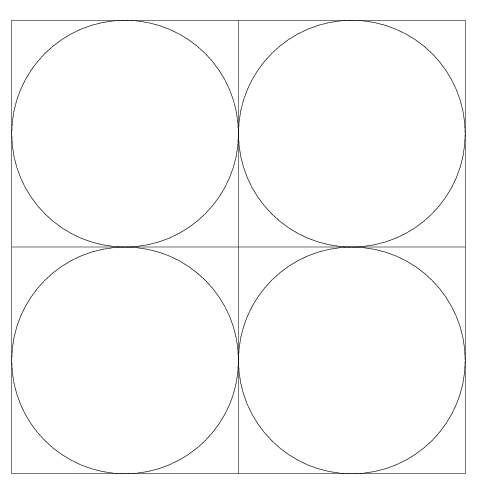
Deuxième méthode

Si un cercle n'est pas la courbe d'une fonction (il peut y avoir 2 $y$ pour un $x$ donné), on peut cependant le voir comme la réunion de deux courbes de fonctions :

Ainsi, la deuxième méthode peut s'adapter en traçant les deux fonctions :

• $f(x) = b - \sqrt{R^2 - (x-a)^2}$
• $f(x) = b + \sqrt{R^2 - (x-a)^2}$

sur son domaine de définition ($x \in [a-R, a+R]$).

PIL.ImageDraw

Ce que vous venez de réaliser a bien évidemment déjà été implanté dans PIL. Découvrez-le ici,

Travaux pratiques

Réobtenez les dessins ci-dessus avec cette bibliothèque, pour vous familiariser à son usage.