WikiMath

On commence cette courte introduction à la notion de chaos par faire l'exposé de quelques exemples classiques, historiquement importants. Chaque exemple apporte un éclairage nouveau pour saisir ce que l'on entend par chaos.

Le modèle de Verhulst

Malthus

Présentation

A la fin du XVIII^ième siècle, un économiste anglais du nom de Thomas Malthus, se fit connaître internationalement par sa vision, assez conservatrice et pessimiste, des rapports entre population et production.

Ce dernier prédit une croissance exponentielle de la population (par exemple : 1, 2, 4, 8, 16, 32, ...) alors que les ressources ne croissaient que de façon arithmétique (1, 2, 3, 4, 5, 6, ...) D'où des catastrophes démographiques, à moins d'empêcher la population de croître.

Formulation mathématique

Malthus suppose donc que, si $P_0$ désigne la population initiale, $P_n$ celle au bout de $n$ années, alors

$P_{n+1} = k P_n$

(pour $k = 2$, on trouve un doublement de la population d'une année à l'autre, quand pour $k=1,05$, on obtient une augmentation de 5%).

On préfère souvent exprimer l'accroissement relatif de la population, que l'on trouve dans ce modèle égale à

$\frac{P_{n+1}-P_n}{P_n} = k-1$

(pour $k=1,05$, on trouve un accroissement relatif de 5%.)

Travaux pratiques

1. Cherchez une valeur possible de $k$, en regardant dans le tableau suivant quelle était la population de la France en $P_0 = 1795$ et en $P_6 = 1801$.

1. Tracez l'évolution de la population française entre 1795 et aujourd'hui :
   • d'après le modèle de Malthus,
   • d'après les valeurs issues de wikipédia.

Ce modèle a, par la suite, été amélioré par Verhulst...

Le modèle de Verhulst

Pour Verhulst, l'accroissement relatif de la population est une fonction décroissante de cette population. Il choisit, en 1845, la plus élémentaire des fonctions pour son modèle : une fonction affine, ce qui donne l'expression suivante :

$\frac{P_{n+1}-P_n}{P_n} = a \left( 1- \frac{P_n}{b} \right)$

où $a$ et $b$ sont des constantes positives. On retrouve :

• à gauche de cette égalité, l'accroissement relatif de la population : la variation de la population en une année, rapportée à la population de cette année,
• à droite, le fait que cet accroisement relatif est supposé être une fonction affine, à pente négative, de la population $P_n$.

Travaux pratiques

1. Exprimez $P_{n+1}$ en fonction de $P_n$.
2. Représentez la nouvelle évolution de la population, sur votre précédent graphique. Le résultat est-il meilleur ?

Critique du modèle

Ce modèle n'est pas si mauvais, puisqu'il avait prévu, en son temps, qu'en 1930 il y aurait 40 millions de Français (en réalité, ils étaient 41,1 millions).

L'intérêt du modèle est cependant moins la prospective, que la découverte des nouvelles propriétés topologiques qu'il induit.

Première apparition de la fonction logistique

En regardant de plus près le comportement de la suite des $P_n$ pour diverses valeurs de $a~$ et $b$, Verhulst entrevoit des situations fort différentes.

En effet,

• ou cette suite a une limite,
• ou ses termes passent d'une limite à l'autre, en une sorte de cycle a deux éléments, un 2-cycle.

• Il peut même y avoir naissance de 4-cycles, puis de 8-cycles, etc.

Verhulst est le premier à avoir représenté graphiquement un diagramme de bifurcation.

Henri Poincaré

Il faudrait, pour respecter le cheminement de l'histoire des idées concernant la théorie du chaos, parler ici d'Henri Poincaré, un des plus grand mathématiciens du XX^ième siècle, qui est aussi l'un précurseur de cette dernière théorie.

Hélas, ses travaux sont trop complexes pour être ici abordés. Aussi, nous sautons son étude fondamentale du problème à trois corps, en signalant toutefois qu'il illustre...

• L'impossibilité pratique de résoudre numériquement certains problèmes physiques (en l'occurence, le devenir de trois corps célestes soumis à leur attractions gravitationnelles respectives), du fait que certains systèmes, qualifiés depuis de chaotiques, ont la facheuse propriété de multiplier à l'infini d'infimes erreurs initiales,
• La possibilité, pourtant, de trouver qualitativement certaines propriétés de ces systèmes (tout n'est pas perdu).

Une cinquantaine d'années plus tard, après l'apparition de l'informatique comme outil de calcul, un autre système chaotique est apparu, dans la méthéorologie.

L'effet papillon

Introduction du système de lorenz

En 1963, le météorologue Edward Lorenz, mort récemment, est le premier à mettre en évidence le caractère vraisemblablement chaotique de la météorologie.

Mathématiquement, le couplage de l'atmosphère avec l'océan est décrit par l'équation de Navier-Stokes de la mécanique des fluides. Ce système d'équations était beaucoup trop compliqué à résoudre numériquement pour les premiers ordinateurs, existant au temps de Lorenz.

Celui-ci simplifia donc le plus possible ces équations, et étudia de ce fait numériquement une situation physique très particulière, le phénomène dit de convection de Rayleigh-Bénard, assimilant en gros les flux d'air de notre atmosphère à ce qui se passe lorsque de l'eau chauffe dans une casserole couverte.

Il aboutit alors à un système dynamique différentiel possédant seulement trois degrés de liberté, beaucoup plus simple à résoudre numériquement que les équations de départ.

Le système de lorenz

Présentation

Ce système différentiel s'écrit :

$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=\sigma \left( y(t) - x(t) \right)$

$\frac{\mathrm{d}y(t)}{\mathrm{d}t}=\rho \, x(t) - y(t) - x(t) \, z(t)$

$\frac{\mathrm{d}z(t)}{\mathrm{d}t} =x(t) \, y(t) - \beta \, z(t)$

où $x, y$ et $z$ sont les grandeurs physiques qui nous intéressent, et $\sigma$, $\rho$ et $\beta$ les paramètres du systèmes, qui sont connus.

Travaux pratiques

Servez-vous de scipy, dont l'utilisation est détaillée dans le tp suivant, à la section 4, pour tracer les solutions de ce système dynamique.

Système dynamique discret de Lorenz

Pour en obtenir une représentation graphique, il faut le discrétiser par une méthode de type Euler : remplacer $\frac{d x(t)}{dt}$ par $\frac{x_{i+1}-x_i}{\delta t}$, où $\delta t$ représente un petit temps.

On obtient alors le système discret :

$\left\{ \begin{array}{ccl} x_{i+1} & = & \delta t . \sigma (y_i-x_i)+x_i \\ y_{i+1} & = & \delta t . (\rho x_i -y_i - x_i z_i) + y_i\\ z_{i+1} & = & \delta t . (-\beta z_i + x_iy_i) + z_i\\ \end{array} \right.$

La légende veut que, travaillant avec ce système, et reprenant un calcul interrompu la veille, avec des conditions initiales très voisines (il ne recopia pas toutes les décimales), Lorenz eut la surprise d'aboutir à une situation complètement différente, très rapidement.

Concrètement, si on place dans nos équations non pas les valeurs exactes des grandeurs physiques concernées (pression athmosphériques, etc.), mais des approximations, alors la prévision du temps qu'il fera change du tout au tout.

D'autres part, pour $\sigma = 10$, $\rho = 28$, $\beta = 8/3$; $\delta t = 0.01$ et pour $(x_0,y_0,z_0)$ le triplet (8,3,4), le système dynamique différentiel de Lorenz présente un superbe attracteur étrange en forme d'ailes de papillon, représenté sur la figure ci-dessous.

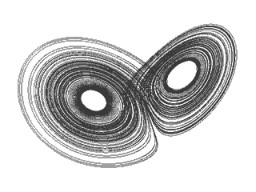
L'attracteur étrange

En d'autres termes, supposons que l'on parte d'un point $(x_0, y_0, z_0)$ de l'espace, représentant certaines conditions atmosphériques au jour d'aujourd'hui, et que l'on place les différents $(x_n, y_n, z_n)$ dans l'espace, qui représentent l'évolution de ces conditions atmosphériques...

• On peut difficilement prévoir où tomberont les prochains termes, et plus l'on souhaite regarder loin, moins nos prévisions ont de chances de se réaliser.
• Seulement, au fur et à mesure que nos points apparaissent sur le graphe, on découvre qu'une figure étrange se dessine.

Le système boucle plusieurs fois autour du point central d'une des deux ailes, puis passe sans prévenir à l'autre aile, sur lequel il va boucler un nombre imprévisible de fois, avant de revenir à sa première aile, etc.

Apparaissent ainsi deux propriétés fondamentales des systèmes chaotiques : l'imprédictibilité, et l'existence potentielle d'un attracteur étrange. D'autres part...

La sensibilité aux conditions initiales

Si l'on part d'un autre point, très voisin de l'ancienne condition initiale, on part donc d'une autre ligne de notre papillon, qui s'enroulera un nombre différent de fois sur chaque aile, prenant donc très vite un chemin complètement différent du précédent.

Pour presque toutes les conditions initiales (différentes de celles des points fixes), l'orbite du système se promène sur l'attracteur, la trajectoire commençant par s'enrouler sur une aile, puis sautant d'une aile à l'autre pour commencer à s'enrouler sur l'autre aile, et ainsi de suite, de façon apparemment erratique.

Cette sensibilité aux conditions initiales est intimement liée au caractère imprévisible du système.

Chez Lorenz, l'intervention de l'ordinateur est cruciale. La sensibilité aux conditions initiales est en effet révélée par le biais de l'instabilité d'un calcul numérique. Les variations infimes entre deux situations initiales pouvaient conduire à des situations finales sans rapport entre elles.

L'effet papillon

C'est en 1972 qu'Edward Lorenz présente l'effet papillon devant l'Association Américaine pour le progrès des Sciences. Sa question demeure célèbre : Le battement d'aile d'un papillon au Brésil peut-il déclencher une tornade au Texas ?

Le papillon, plutôt que la coccinelle, est choisi ici pour faire un parallèle avec la forme de l'attracteur étrange.

Lorenz affirma ainsi qu'il n'était pas envisageable de prévoir correctement des modifications climatiques à long terme. En effet, une incertitude de $10^{-6}$ lors

• des mesures physiques des grandeurs intervenant dans le système (pression atmosphérique, température, etc.),
• ou de la saisie des données de la situation actuelle du temps,

peuvent conduire à une prévision totalement erronée : deux points extrêmement proches, sur l'attracteur, pouvaient avoir des comportements complètement différents.

Or ces incertitudes sont inévitables : l'homme ne peut pas prendre en compte tous les éléments qui constituent son environnement, surtout lorsque de telles variations infimes deviennent si importantes.

Simple et complexe

Lorenz découvrit donc qu'une dynamique très complexe peut apparaître dans un système formellement très simple.

L'appréhension des rapports du simple et du complexe s'en trouve profondément bouleversée.

En particulier, on s'aperçoit que la complexité peut être intrinsèque à un système. Jusque-là on la rapportait plutôt à un caractère extérieur, accidentel, lié à une multitude de causes.

Travaux pratiques

1. Représentez l'attracteur étrange de Lorenz.
2. Variez légèrement les conditions initiales, et faites apparaître l'un après l'autre les points de ce système, pour illustrer la sensibilité aux conditions initiales.

Le chat d'Arnold

L'application « chat » d'Arnold (1968)

On découvrit alors d'autres systèmes dynamiques discrets, plus simples encore que celui de Lorenz, et qui possédaient eux-aussi des éléments de type chaos :

• existence éventuelle d'un attracteur étrange,
• imprédictibilité, sensibilité aux conditions initiales,

Le chat d'Arnold en est un célèbre exemple.

Le nom d'application « chat » provient d'un jeu de mot anglais intraduisible en français : en effet, « chat » se dit « cat » en anglais, et Arnold utilisait ce mot comme abréviation de : « Continuous Automorphisms of the Torus », littéralement : « automorphismes continus sur le tore ».

L'application chat d'Arnold est une application du carré [0, 1] x [0, 1] dans lui-même définie par : $\left\{\begin{array}{ccl} x_{n+1} & = & x_n + y_n \mod 1 \\ y_{n+1} & = & x_n + 2 y_n \mod 1 \end{array}\right.$

Ces itérations sont simples, formellement, et se représentent facilement...

Représentation des itérations

  >>> from pylab import plot show
  >>> X,Y=[0.3],[0.2]
  >>> for k in range(100):
  ...     xn=X[len(X)-1]
  ...     yn=Y[len(Y)-1]
  ...     X.append((xn+yn)%1)
  ...     Y.append((xn+2*yn)%1)
  ...
  >>> plot(X,Y,'o')
  >>> show()

Le chaos du chat

Pourtant...

• On ne peut pas prévoir où tombera le prochain point.
• Aucune logique habituelle n'apparaît dans la dynamique : ni convergence vers un point, ni divergence, ni apparence de cycle.
• Quand on augmente le nombre de points, on remarque que tout le plan est parcouru.

Ici, pas d'attracteur étrange. Au lieu d'être dans la situation classique d'une convergence, d'une divergence ou d'un cycle, on s'aperçoit que ce système tape partout dans le carré, sans que l'on soit capable de prévoir où tombera le prochain terme. La répartition est uniforme et imprévisible : on est en plein chaos.

Le diagramme de Hénon

Le diagramme de Hénon décrit les astéroïdes gravitant autour du soleil, ou l'eau qui s'égoute du robinet. Il possède un attracteur étrange.

L'attracteur de Hénon prend tout point du plan (x, y) et lui associe le nouveau point :

$\left\{\begin{array}{ccl}x_{n+1} & = & y_n+1-a x_n^2\\ y_{n+1} & = & b x_n\\ \end{array}\right.$

Il dépend de deux paramètres, a et b, qui ont pour valeurs canoniques : a = 1.4 et b = 0.3.

C'est l'un des systèmes dynamiques ayant un comportement chaotique les plus étudiés. Pour plus de détails : ici.

Sujet de TP

Représentez l'attracteur de Hénon, et visualisez l'attracteur étrange.