WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Systemes Dynamiques
Le but du présent TP est de découvrir les systèmes dynamiques (système proies-prédateurs, modélisations d'épidémies).
En général, on ne sait pas les résoudre exactement. On présente donc les études qualitatives, et les méthodes approchées qui permettent d'obtenir toutes sortes d'informations sur les solutions de ces systèmes.
Les modèles proies-prédateurs
Le modèle de Malthus
Soit $x(t)$ et $y(t)$ le nombre respectif de proies et de prédateurs à l'instant $t$.
Le modèle de Malthus (1766-1834) suppose une croissance exponentielle des proies en l'absence de prédateurs : $\frac{dx}{dt} = a x(t)$ et une décroissance exponentielle des prédateurs en l'absence de proies : $\frac{dy}{dt} = -c y(t)$
Le système de Lokta-Volterra
Une hypothèse supplémentaire conduit au système de Lokta-Volterra (1918-1939) : les taux de disparition des proies et de croissance des prédateurs sont proportionnels au nombre $x(t)y(t)$ de rencontres entre les deux populations. $ \left\{ \begin{array}{ll} \frac{dx}{dt} & = a x(t) - b x(t) y(t) \\ \frac{dy}{dt} & = -c y(t) + d x(t) y(t) \\ \end{array} \right. $
Etude qualitative
Existence et unicité d'une solution
La fonction du système : $f(x,y) = (x(a-by);y(-c+dx))$ est $C^1$.
Sous ces conditions, le théorème de Cauchy-Lipschitz affirme l'existence d'une solution maximale au problème ($u=(x,y)$) : $\left\{ \begin{array}{ll} u'(t) & = f(u(t))\\ u(0) & = u_0 \end{array} \right. $ dans $C \left( [O, T^*[, \mathbb{R}^2 \right)$.
Il suffit que $f$ soit localement lipschitzienne (localement, tout segment reliant deux points de son graphe a une pente inférieure à une constante donnée) pour appliquer ce théorème.
Existence globale
Résultat
De plus, comme la solution maximale $u(t) = (x(t), y(t))$ est bornée, un théorème affirme l'existence globale des solutions : $T^* = + \infty$.
Démonstration
On a $y' (ax-bxy) = x' (-c+dxy)$ soit $y'(a-by)/y=x'(dx-c)/x$ D'où $H(x,y)=dx-c lnx + by - a ln x$ est une intégrale première du système : pour toute solution $(x(t),y(t)), H(x(t),y(t)) = C^{te}$
Par passage à l'exponentielle, $A(x) B(y) = D (C^{te})$ avec $A(x) = x^c e^{-dx}$ et $B(y) = y^a e^{-by}$.
Une étude de fonction prouve que $A(x)$ admet un maximum $M_A$ en c/d, et tend en décroissant vers 0 quand $x \rightarrow + \infty$. De même, $B(y)$ admet un max $M_B$ en a/b, et tend vers 0.
Comme $0 \leqslant D \leqslant M_A M_B, \exists T \in [0, M_A], D = T M_A$. Si $x$ est non bornée, alors $x \rightarrow +\infty$, et d'après le théorème des valeurs intermédiaires, $\exists t_0, A(x(t_0)) \leqslant T/2$, et donc $B(y(t_0)) = D/A(x(t_0)) \geqslant 2 M_B$.
Ceci est absurde (le max de $B$ est $M_B$), donc $x$ est borné. Pareil pour $y$.
Recherche de points stationnaires
Les points stationnaires
Pour trouver des points stationnaires, on résoud le système :
$ \left\{ \begin{array}{ll} ax - b xy & = 0 \\ -cy + d xy & = 0 \end{array} \right. $
On trouve les points $(0,0)$ et $(c/d, a/b)$.
Stabilité de $(0,0)$
On a résultat suivant :
Théorème : Si $f$ est différentiable en $(0,0)$, et $f(0) = 0$, alors... S'il existe une valeur propre de $D_f(0)$ à partie réelle strictement positive, alors le point 0 est instable.
Ici, $D = \left( \begin{array}{cc} a-by & -bx \\ dy & -c+dx \end{array}\right)$ donc $D_f(0,0)$ a une valeur propre de partie réelle $>0$ : $(0,0)$ est un point d'équilibre instable.
En clair, si l'on part d'un point voisin de $(0,0)$, par exemple si au départ on n'a qu'un tout petit peu de proies et de prédateurs, alors on s'éloigne de cette configuration.
Stabilité de $(c/d,a/b)$
Un peu de théorie
Définition : Soit $U$ un voisinage de $0$, et $V : U \rightarrow \mathcal{R}$ une fonction continue et différentiable sur $U \setminus \{0 \}$, telle que :
- $V(0) = 0$ et si $u \neq 0, V(u) > 0$,
- $\forall u \notin U \setminus \{ 0 \}$, le produit scalaire entre $f(u)$ et le gradient de $V(u)$ est négatif.
Alors on dit que cette fonction est une '''fonction de Lyapunov .
Théorème : S'il existe une fonction de Lyapunov pour le système, alors le point d'équilibre est stable.
Ici, $V(x,y) = H(x,y) - H(c/d, a/b)$ est une fonction de Lyapunov, donc $(c/d, a/b)$ est stable.
Démonstration
$\bigtriangledown V(x,y) = (d-c/b, b-a/y)$, donc le produit scalaire entre $f(u)$ et $\bigtriangledown V(u)$ est nul.
De plus, $V(x,y) \geqslant 0$, et $V(x,y) = 0 \Longleftrightarrow (x,y) = (c/d, a/b)$.
Périodicité
Les solutions du système de Lotka-Volterra sont périodiques.
La démonstration de ce point n'est pas très compliqué. Il me manque juste le courage et le temps pour la faire figurer ici :)
Solutions exactes
On ne sait pas calculer une solution exacte du système de Lotka-Volterra à l'aide d'une formule analytique. C'est pourquoi les méthodes de résolution numériques sont intéressantes...
Les méthodes approchées
La méthode d'Euler
La méthode
Elle consiste à approcher la fonction solution du problème $\left\{ \begin{array}{ll} u'(t) & = f(u(t))\\ u(0) & = u_0 \end{array} \right. $ par une fonction affine par morceaux, de la façon suivante : on confond la courbe de la fonction solution sur [$t_n ; t_{n+1}$] avec sa tangente en $(t_n, y(t_n))$.
Comme $y(t) = y(t_n) + (t-t_n) y'(t_n)$ sur [$t_n ; t_{n+1}$], on a alors $y(t) = y(t_n)+(t-t_n) f(t_n, y(t_n))$
Partant de $y_0 = y(t_0)$, on calcule $y(t_n)$ par : $y(t_{n+1}) = y(t_n)+(t_{n+1}-t_n) f(t_n, y(t_n))$
Application à un circuit RC
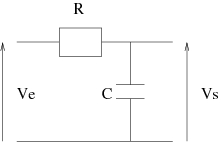
Une loi des mailles donne : $Ve = RC \frac{d Vs}{dt} + Vs$, soit $\frac{d Vs}{dt} = \frac{1}{RC} (Ve-Vs)$.
L'algorithme d'Euler donne alors : $Vs(n+1) = Vs(n) + \frac{1}{RC} (E-Vs(n)) \Delta T$ où $Vs(n)$ est l'approximation de $Vs(t)$ au temps $t_n = t_0 + n \Delta T$.
Application au système proies-prédateurs
Mise en équation
On écrit le système d'équations du modèle proies-prédateurs
$ \left\{ \begin{array}{ll} \frac{dx}{dt} & = a x(t) - b x(t) y(t) \\ \frac{dy}{dt} & = -c y(t) + d x(t) y(t) \\ \end{array} \right. $ sous la forme de la méthode d'Euler $\left\{ \begin{array}{ll} u'(t) & = f(u(t))\\ u(0) & = u_0 \end{array} \right. $ ...en posant $u=(x,y)$ et $f(x,y)=(x (a-by),y (-c+d x))$
Pour pouvoir faire des calculs, on donne des valeurs à $a,b,c,d$ : respectivement $3,1,2,1.$
Préliminaires
On commence par importer les modules numpy (pour le type array) et pylab (pour le tracé de courbes) :
>>> from numpy import * >>> from pylab import *
Puis on définit la fonction et le pas du système :
>>> def f(X): ... return array((X[0]*(3-X[1]),X[1]*(-2+X[0]))) ... >>> h=0.05
Méthode d'Euler
On peut maintenant programmer la méthode d'Euler, ie calculer la suite $X_0 = (1,2), X_{n+1} = X_{n} + h f(X_n)$ pour 200 valeurs (le vecteur $X$ contient les $(x_n,y_n)$) :
>>> X=zeros((2,200),float) >>> X[:,0]=array((1.,2.)) >>> for k in range(199): ... X[:,k+1]=X[:,k]+h*f(X[:,k]) ...
Evolution en fonction du temps
On trace maintenant l'évolution du nombre de proies et de prédateurs en fonction du temps :
>>> plot(X[0,:]) >>> plot(X[1,:]) >>> title(``Methode d'Euler'') >>> show()
Résultats
Evolution du nombre de proies et de prédateurs en fonction du temps
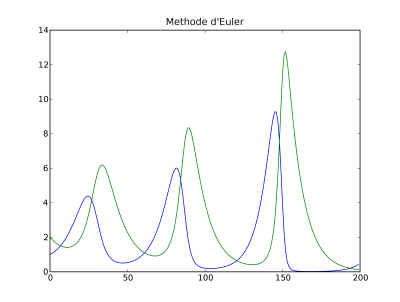
Diagramme de phase
...puis le diagramme de phase :
>>> figure()
>>> plot(X[0,:],X[1,:])
>>> title('Portrait de phase')
>>> xlabel('x')
>>> ylabel('y')
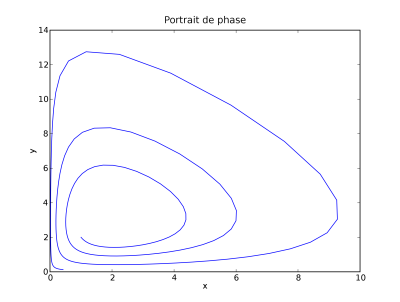
Vers une meilleure méthode
Les résultats ne sont pas conformes à notre étude théorique : les nombres de proies et de prédateurs devraient varier périodiquement.
On va donc utiliser une meilleure méthode de résolution : la méthode de Runge-Kutta.
Runge-Kutta
Introduction à la méthode
Les méthodes de Runge-Kutta sont des méthodes d'analyse numérique d'approximation de solutions d'équations différentielles. Elles portent le nom des mathématiciens Carl Runge et Martin Wilhelm Kutta.
Ces méthodes reposent sur le principe de l'itération, c'est-à-dire qu'une première estimation de la solution est utilisée pour calculer une seconde estimation, plus précise, et ainsi de suite.
$RK_4$
La méthode de Runge-Kutta classique d'ordre quatre est un cas particulier d'usage très fréquent, noté $RK_4$.
Considérons le problème suivant : $y' = f(t, y), \quad y(t_0) = y_0 $
La méthode $RK_4$ est donnée par l'équation $y_{n+1} = y_n + \frac{h}{6} (k_1 + 2k_2 + 2k_3 + k_4) $
où
- $k_1 = f \left( t_n, y_n \right) $
- $k_2 = f \left( t_n + \frac{h}{2}, y_n + \frac{h}{2} k_1 \right) $
- $k_3 = f \left( t_n + \frac{h}{2}, y_n + \frac{h}{2} k_2 \right) $
- $k_4 = f \left( t_n + h, y_n + h k_3\right)$
Principe
L'idée est que la valeur suivante ($y_{n+1}$) est approchée par la somme de la valeur actuelle ($y_n$) et du produit de la taille de l'intervalle ($h$) par la pente estimée.
La pente est obtenue par une moyenne pondérée de pentes :
- $k_1$ est la pente au début de l'intervalle ;
- $k_2$ est la pente au milieu de l'intervalle, en utilisant la pente k1 pour calculer la valeur de y au point $t_n + h/2$ par le biais de la méthode d'Euler ;
- $k_3$ est de nouveau la pente au milieu de l'intervalle, mais obtenue cette fois en utilisant la pente $k_2$ pour calculer $y$;
- $k_4$ est la pente à la fin de l'intervalle, avec la valeur de $y$ calculée en utilisant $k_3$.}
Moyenne des quatre pentes
Dans la moyenne des quatre pentes, un poids plus grand est donné aux pentes au point milieu : $pente = \frac{k_1 + 2k_2 + 2k_3 + k_4}{6}.$
La méthode $RK_4$ est une méthode d'ordre 4, ce qui signifie que l'erreur commise à chaque étape est de l'ordre de $h^5$, alors que l'erreur totale accumulée est de l'ordre de $h^4$.
Ces formules sont aussi valables pour des fonctions à valeurs vectorielles.
Programmation
On passe maintenant à la programmation de cette méthode :
>>> X=zeros((2,200),float) >>> X[:,0]=array((1.,2.)) >>> for k in range(199): ... k1=f(X[:,k]) ... k2=f(X[:,k]+h/2*k1) ... k3=f(X[:,k]+h/2*k2) ... k4=f(X[:,k]+h*k3) ... X[:,k+1]=X[:,k]+h/6.*(k1+2*k2+2*k3+k4) ...
On peut alors reprendre la fin du code précédent pour tracer l'évolution en fonction du temps, et le portrait de phase.
Résultats
Evolution du nombre de proies et de prédateurs en fonction du temps

Portrait de phase : évolution du nombre de proies en fonction du nombre de prédateurs

Conclusion de l'étude approchée
Des données concernant les captures de lynx et de lièvres, collectées au Canada entre 1845 et 1955, mettent en évidence les variations cycliques que l'on a obtenu :
- Lorsque les deux animaux sont rares, les lièvres trouvent facilement à se nourir, et subissent peu de prédation : ils prolifèrent.
- Les lynx, trouvant d'avantage de proies, se multiplient à leur tour.
- Donc la prédation des lièvres devient importante, et la population de ces derniers chute.
- Donc les lynx, à leur tour, disparaissent, par manque de nourriture.
- etc.
Utilisation de scipy
Ces méthodes de résolution numérique d'une équation différentielle sont déjà programmées dans le module scipy.
Pour tracer les courbes, on importe pylab, et pour la fonction odeint résolvant des équations différentielles...
>>> from pylab import * >>> from scipy.integrate import odeint
Dérivée et trajectoire
On définit alors notre fonction dérivée :
>>> def derivee(y,t): ... """ Notre fonction derivee """ ... return array([y[0]*(3-y[1]),y[1]*(-2+y[0])])
Puis la fonction calculant la trajectoire solution...
>>> def trajectoire(y0): ... """ On integre notre equation differentielle ... ordinaire avec le point initial y0 """ ... t=arange(0.0,100.0,0.1) ... y = odeint(derivee,y0,t) .... return y[:,0],y[:,1]
Tracé
Il reste plus qu'à tracer le tout :
>>> proieA, predA = trajectoire([1.0,0.9])
>>> proieB, predB = trajectoire([0.9,0.9])
>>> plot(proieA, predA)
>>> plot(proieB,predB, "r--")
>>> xlabel("proies")
>>> ylabel("predateurs")
>>> show()
Améliorations possibles
Rafiner le modèle
Pour rafiner le modèle, on peut supposer que le taux de croissance des proies diminue lorsque la population de proies augmente : compétition pour la nourriture, l'espace, etc.
En l'absence de prédateurs, cela se traduit par $\frac{x'}{x} = a \left(1- \frac{x}{L} \right)$ où la constante $L$ représente la population maximale de proies.
Nouveau système
Le modèle devient alors :
$\left\{ \begin{array}{ll} \frac{dx}{dt} & = ax - b xy - \frac{a}{L} x^2\\ \frac{dy}{dt} & = - c y + d xy\\ \end{array} \right. $
qui admet $(0,0)$ et $(c/d, a/b - ac/(Lbd))$ pour points d'équilibres.
Résultats
Evolution du nombre de proies et de prédateurs en fonction du temps
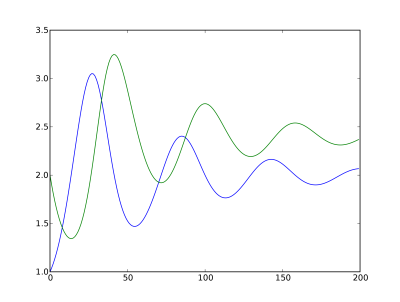
Portrait de phase
Evolution du nombre de proies en fonction du nombre de prédateurs

Autres exemples de modélisation
Propagation des épidémies
La peste
La peste est causée par une bactérie : Yersinia pestis. L'identification d'un microbe responsable s'est faite par étapes successives durant la fin du XIXième. Lors de l'épidémie, la transmission peut se faire par voie respiratoire inter-humaine, par morsure ou par piqûre.
Il y a plusieurs types de pestes : bubonique, septicémique et pneumonique (ou pulmonaire).
La peste en Europe
En Europe, la dernière grande épidémie remonte à 1720 à Marseille : le Grand-Saint-Antoine entre au port. Un passager clandestin a la peste.
Les médecins du port ne décrètent qu'une quarantaine "douce"... et la moitié des 80000 Marseillais en sera victime.
Début de modélisation
On simplifie le plus possible notre modèle, pour pouvoir commencer notre modélisation.
On suppose qu'il n'y a pas de décès, pas de guérison, pas d'isolement ; un malade reste alors toujours malade et contagieux.
Si on note $x$ les réceptifs (ou susceptibles) et $y$ les contagieux, on obtient $\frac{d x}{dt} = - \beta xy, \frac{d y}{dt} = \beta xy$ avec :
- $\beta$ représentant la probabilité de propagation du virus entre un infecté et un susceptible,
- et $x+y = n$ : la population totale.
Ce système s'intègre exactement.
Modèle de Kormack et McKendrick
Si l'on rajoute les sujets qui s'en sont sortis, et se retrouvent immunisés, on trouve le modèle de Kormack et McKendrick $\frac{d x}{dt} = - \beta xy, \frac{d y}{dt} = (\beta x- \gamma ) y, \frac{d z}{dt} = \gamma y$ $\gamma$ représente la probabilité pour un infecté de guérir, et $x+y+z = n$.
L'épidémie n'a lieue que si le nombre de réceptifs $x_0$ est inférieur au seuil $\gamma / \beta$.
Dans ce modèle SIR (Susceptible, Infected and Recovered) de 1947, optimiste, les malades tendent vers 0.
Vers plus de réalisme
On peut, pour rendre ce modèle un peu plus réaliste, rajouter les morts $m(t)$ : $y'(t) = \beta xy - \gamma y - \delta y$ où $\delta y$ est le nombre de personnes infectées qui vont mourir (le nombre de morts naturelles est négligeable face à ce qui se passe avec la peste), et alors $m'(t) = \delta y$.
Pour les conditions initiales : $\gamma \approx 1$ et $\delta \approx 0$. Si la population est en bonne santé, $\beta \approx 0$.
Conclusion
La peste noire (1347-1351) a causé la mort d'au moins un tiers de la population européenne (25 millions de victimes).
Elle est toujours d'actualité. La peste est une des maladies bactériennes les plus dangereuses pour l'humanité, et est actuellement en recrudescence. Près de 30 000 cas de peste ont été déclarés depuis une dizaine d'années.
Equation de Van der Pol
Des analogies
Les équations qui réglent le mouvement d'un pendule élastique, et la charge d'un condensateur dans un circuit RLC série, sont formellement analogues.
On peut passer de l'une à l'autre par simple changement de notation.
Dissipation d'énergie
Dans un circuit RLC série, l'énergie électrique ne se conserve pas au cours du temps ; elle se dissipe par effet Joule dans la résistance.
De la même manière, l'énergie mécanique d'un oscillateur élastique ne se conserve pas au cours du temps : elle est dissipée par frottement de type fluide visqueux.
Des oscillations électriques ou mécaniques s'amortissent de ce fait.
Entretient des oscillations
Si l'on veut entretenir les oscillations, il faut un apport constant d'énergie pour compenser les pertes.
L'utilisation d'un circuit à amplificateur opérationnel permet de simuler un dipôle à résistance négative obéissant à la loi d'Ohm : $u=-R_N i$.
La résistance négative est l'élément capital qui permet d'entretenir, par apport d'énergie extérieure, les oscillations d'un système physique qui, sans elle, s'amortirait inévitablement.
Non-linéarité de l'équation
La stabilisation des oscillations amorcées par une résistance négative exige dans le système des éléments non linéaires.
Dans le cas de simulation de résistance par un circuit à amplificateur opérationnel, c'est le phénomène de saturation en tension de sortie qui assure la non-linéarité indispensable à la stabilisation de l'oscillateur.
Le circuit à amplificateur opérationnel se comporte comme un puits de résistance négative, linéaire par morceaux.
L'équation de Van der Pol
Van der Pol eut l'idée d'approcher ce puits par une fonction parabolique :
$\left\{ \begin{array}{l} \frac{d^2 u}{d t^2} - \frac{w_0}{Q} \left( 1 - \frac{u^2}{A^2} \right) \frac{du}{dt} + w_0^2 u = 0\\ w_0^2 = \frac{1}{LC}, A=r i_0 \sqrt{\frac{R_0-r}{R_0}} \end{array} \right.$
Travaux pratiques
Faire l'étude améliorée du système proies prédateurs : on retrouvera les graphes proposés précédement en utilisant pylab, et en reprogrammant les méthodes d'Euler et de Runge-Kutta.
Faire le même type d'étude quantitative pour la propagation de la peste et le modèle de Van der Pol.
Tenter une étude qualitative de ces problèmes.