WikiMath

---

Principe de la méthode

Le principe de la méthode repose sur le fait qu'une fonction continue ne peut changer de signe qu’en prenant la valeur 0. C'est le principe des valeurs intermédiaires.

1. On choisit un intervalle [a, b] tel que $f(a) \times f(b) < 0$. Cet intervalle contiendra donc au moins une solution (si $f$ est strictement monotone sur [a, b], on a une solution unique).
2. Diviser par 2 la longueur de l’intervalle encadrant la solution cherchée : $c = \frac{a+b}{2}$, et calculer $f(c)$.
3. Un seul des trois cas suivants est possible :
   • $f(c) = 0$ (à $\epsilon$ près) : alors $c$ est la solution recherchée.
   • $f(a) \times f(c) <0$ : alors la solution est dans l'intervalle [$a,c$].
   • $f(a) \times f(c) > 0$ : alors la solution est dans l'intervalle [$c,b$].
4. Le procédé est à recommencer autant de fois que nécessaire.

A chaque itérée, nous divisons par 2 la longueur de l'intervalle encadrant la solution recherchée, il y a donc convergence.

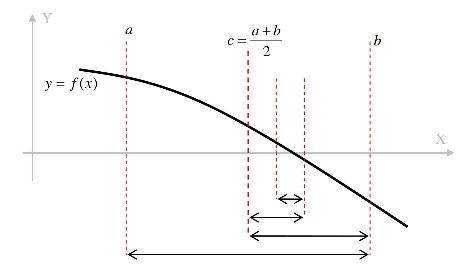
On itère le processus jusqu'à ce que la longueur de l’intervalle obtenu soit assez petit pour nous donner la solution avec la précision recherchée.

Travaux pratiques

Mise en application sur un exemple

Trouvez la valeur $s$ pour laquelle $f(x) = x^3-x-1$ s'annule...

1. On pourra commencer à chercher où la dérivée s'annule, à la main, afin d'obtenir un tableau de variations de $f$.
2. Ce tableau de variations permet d'obtenir les valeurs de départ ($a$ et $b$) de la recherche dichotomique : ils doivent être tels que $f$ n'ait pas le même signe en $a$ qu'en $b$.
3. Rechercher un encadrement de $s$ à $10^{-3}$ près, puis à $10^{-5}$ près, par la méthode dichotomique.

Refaire le travail avec différentes fonctions de votre choix.

Réalisation d'une fonction

Faire une fonction dichoto, qui reçoit en argument :

• la fonction $f$ dont on cherche une racine,
• les valeurs $a$ et $b$ de départ de la recherche,
• la condition d'arrêt,

et qui renvoie la solution issue de la recherche dichotomique.

La condition d'arrêt pourra être, au choix :

• le nombre d'itérations $n$ à effectuer.
• la précision $\epsilon$ souhaitée.

Rechercher le lien (la formule) entre ces deux conditions d'arrêts $\epsilon$ et $n$.

(Solution)