WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Methodes Elementaires
On souhaite calculer
$\displaystyle{\int_a^b f(x) dx}$
où $f$ est continue sur [$a, b$], c'est-à-dire calculer l’aire algébrique comprise entre :
- la courbe,
- l'axe des $x$,
- et les verticales $y=a, y=b$,
On peut procéder ainsi :
- Diviser l’intervalle [$a, b$] en $n$ sous-intervalles égaux [$x_i , x_{i+1}$], où $i \in \{0,... , n-1\}$. Ces $x_i$ valent :
$x_i = a + \frac{b-a}{n} \times i$.
- Approximer, sur chaque sous-intervalle, la fonction $f$ par une fonction « facile à intégrer », c'est-à-dire dont la surface se calcule aisément.
On pourra remplacer, sur chaque sous-intervalle, la fonction à intégrer par :
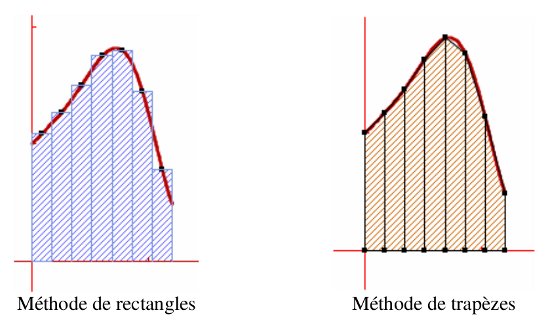
- Une constante, ce qui revient à calculer la surface de rectangles (méthode des rectangles).
- Une fonction affine, ce qui revient à calculer la surface de trapèzes (méthode des trapèzes?).
- Une fonction polynomiale de degré supérieur ou égal à 2.
- etc.
- Enfin, approximer l’intégrale recherchée par la somme des intégrales de ces polynômes sur chacun des intervalles [$x_i, x_{i+1}$].
Cela revient à la calculer sous la forme d'une somme de surfaces élémentaires facilement calculables (somme de rectangles, etc.)