WikiMath

---

Présentation de la méthode

Sur chacun des intervalles [$x_i, x_{i+1}$], la fonction est approchée par le polynôme constant égal à la valeur de $f$ au milieu de [$x_i, x_{i+1}$].

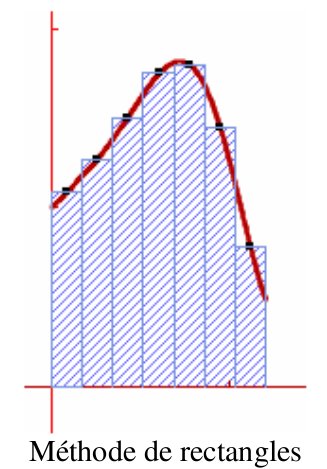
Ceci revient à considérer que :

$\displaystyle{\int_a^b f(x) dx \approx \frac{b-a}{n}\sum_{i=0}^{n-1} f\left(\frac{x_i+x_{i+1}}{2} \right)}$

Le choix du milieu de l’intervalle permet d’espérer que les erreurs par excès et par défaut se compenseront, au moins en partie :

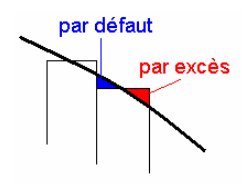
Travaux pratiques

1. Faire une fonction qui reçoit :

• une fonction $f$,
• les bornes de l'intervalle [$a,b$],
• le nombre $n$ de rectangles d'approximation,

et qui renvoie la valeur approchée de l'intégrale de $f$, par la méthode des rectangles.

2. Utilisez cette fonction pour calculer une valeur approchée de l'intégrale

$\displaystyle{\int_0^1 \sqrt{x}-x^2 dx}$

3. Comparer votre valeur à celle retournée par sympy, et faire d'autres comparaisons sur des valeurs de votre choix.

4. Comment varie l'approximation quand $n$ grandit ?