---

On commence par faire quelques rappels sur $\pi$, avant de donner quelques sujets d'étude.

Définitions et propriétés

Quelle définition pour $\pi$ ?

La définition habituelle et historique de ${\pi}$ est : le quotient entre le périmètre et le diamètre d'un cercle quelconque. La notation ${\pi}$ pour ce rapport constant date du XVIII^ième ; elle a été popularisée par Euler.

On peut définir ${\pi}$ d'autres manières, comme par exemple "le double de l'unique racine de l'équation $cos(x)=0$ entre 0 et 2".

Comparaison avec $\sqrt{2}$

Dans tous les cas, ce nombre est moins évident à définir que $\sqrt{2}$ :

• la définition géométrique nécessite la notion de cercle (donc de distance), d'espace euclidien et de longueur de courbe, donc de calcul intégral,
• la seconde définition demande d'avoir précédemment construit la fonction cosinus, c'est-à-dire d'une partie de l'analyse.

Cette remarque commence à nous renseigner de la difficulté intrinsèque au nombre $\pi$, comparativement à d'autres nombres connus.

Sur la constance du rapport : périmètre sur diamètre

Cas d'un espace euclidien

Résultat

Dans un espace euclidien le théorème de Thalès s'applique, donc on peut démontrer que le quotient entre le périmètre d'un cercle et son rayon est indépendant du cercle considéré :

Démonstration

En effet, par Thalès, $\frac{R_{1}}{{I_{1}}^{n}}=\frac{R_{2}}{{I_{2}}^{n}}.$ Or, si ${I_{1}}^{n}$ et ${I_{2}}^{n}$ sont des côtés de polygones réguliers inscrits (à $n$ côtés) aux cercles $C_1$ et $C_2$, alors ${I_{1}}^{n}\rightarrow \mathit{{\pi}}_{1}R_{1}, \mathit{ et }{I_{2}}^{n}\rightarrow \mathit{{\pi}}_{2}R_{2}.$ Donc, par passage à la limite dans l'égalité issue de Thalès, on trouve que $\pi_1 = \pi_2$.

Cas de la géométrie non-euclidienne

En géométrie non-euclidienne, on n'a plus la constance du rapport "périmètre sur diamètre".

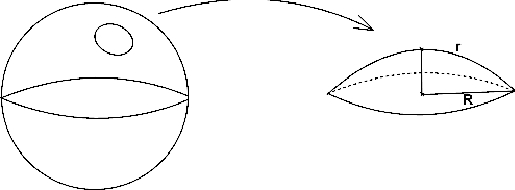
Le rayon (apparent) r du cercle de la figure précédente est strictement plus grand que $R=\frac{P}{2\mathit{{\pi}}}.$

Quelle importance pour nous ?

Notre monde physique n'étant pas euclidien, le rapport du périmètre sur le diamètre d'un cercle varie en fonction du cercle considéré (mais l'erreur est négligeable).

Sous cet angle, on pourrait dire que ${\pi}$ est une constante mathématique, mais pas physique.

Rapport entre surface et carré du rayon d'un cercle

Résultat

Si l'on note respectivement R, P et S les rayon, périmètre et surface d'un cercle, alors $P=2\pi R$ et $S=\pi R^{2}$.

Cela sous-entend que les rapports $\frac{P}{2R}$ et $\frac{S}{R^{2}}$ sont égaux. On peut s'en convaincre en constatant que les surfaces des deux figures suivantes sont égales :

Démonstration de $S=\pi r^2$

Quand on augmente le nombre de "parts" du cercle, la figure associée se rapproche d'un rectangle de longueur ${\pi}$R et de largeur R. En considérant que les aires sont égales, on retrouve l'égalité des deux rapports précédents.

Cette démonstration était connue du monde antique.

Voyons maintenant les raisons qui font que l'on s'intéresse tant à ce nombre, et depuis si longtemps.

Pourquoi $\pi$ plus qu'un autre ?

Raisons historiques

Une longue histoire

On connaît ce nombre depuis quatre millénaires.

La plupart des civilisations l'ont étudié, et certains des plus grands noms de l'humanité - dans le désordre, Ptolémée, Fibonacci, Al-Kashi, Al-Kwarizmi, Newton, Euler, Leibniz, Descartes, Viète, Archimède, Ramanujan et Chudnowsky, etc. - ont cherché des méthodes pour obtenir quelques décimales supplémentaires.

Irrationnel et transcendant

De plus, c'est peut-être le premier irrationnel connu, et assurément le premier nombre transcendant que l'homme ait rencontré.

On rappelle qu'un nombre transcendant est un nombre qui ne peut pas être solution d'une équation polynomiale à coefficients entiers ($e$ en est un exemple, ce qui n'est pas le cas de $\sqrt{2}$). On a beaucoup de mal à "trouver" des nombres transcendants, bien que presque tout nombre réel le soit !

Ce nombre, 4000 ans après, conserve tous ses mystères.

Raisons pratiques

On rencontre ${\pi}$ dans la vie de tous les jours : longueur du fer à fixer sur le tour d'une roue en bois, coût du ruban qui décorera un chapeau, longueur du cerclage d'une barrique, etc.

C'est-à-dire dès qu'il faut calculer le périmètre d'un cercle, les surfaces ou les volumes d'un cylindre, d'un cône, d'une sphère ou d'un tore.

Raisons scientifiques

${\pi}$ est une constante universelle que l'on rencontre un peu partout en mathématique et en physique - mais, étrangement, pas en biologie.

Ainsi, en analyse mathématique :

• ce nombre est intrinsèquement relié à certaines fonctions usuelles (trigonométriques, mais aussi à la fonction ${\Gamma}$ d'Euler),
• en probabilité (dans la loi normale, dans la probabilité pour que deux entiers tirés au hasard soient premiers entre eux, etc.),
• dans la formule fondamentale $e^{i\pi }=-1$
• et dans bon nombre de calculs de séries et d'intégrales, comme par exemple : $\int _{0}^{\infty}e^{-x^{2}}\mathit{dx}=\frac{\sqrt{\mathit{{\pi}}}}{2}$

$\pi$ : un des nombres les plus simples

Et, finalement, ${\pi}$ est peut-être le plus simple nombre transcendant connu : il peut nous aider à mieux comprendre les nombres réels (presque tout nombre est transcendant, on le rappelle).

Ces diverses raisons expliquent l'intérêt porté à ${\pi}$, mais ne justifient pas pourquoi chercher à obtenir sans cesse plus de décimales. En a-t-on réellement besoin d'autant ?

Comment justifier cette quête de nouvelles décimales ?

Pour les calculs scientifiques

Claude Ptolémée (v. 100-v. 170) a eu besoin, dans son Almageste (traité de mathématique et d'astronomie, qui est resté l'ouvrage de référence en la matière, jusqu'à Copernic et Kepler), d'aller jusqu'à la quatrième décimale de ${\pi}$ : il utilisa en effet la valeur sexagésimale $\mathit{{\pi}}=3+\frac{8}{60}+\frac{30}{60^{2}}\simeq 3,14167.$

Mais, si quelques décimales sont nécessaires dans les calculs du monde réel, au-delà de 30 décimales, cette quête devient insensée aux yeux du monde physique, et ne regarde plus que les mathématiques.

Alors, pourquoi les mathématiciens ont-ils besoin de nouvelles décimales ?

Connaître ${\pi}$ en tant que tel

Avant l'irrationalité

Jusqu'en 1761 (date à laquelle Johann Lambert prouva l'irrationalité de ${\pi}$), on cherchait de nouvelles décimales pour trouver une périodicité.

Celui qui aurait vu réapparaître indéfiniment une même succession de chiffres aurait pu, à juste titre, porter le nom de découvreur de ${\pi}$, puisqu'alors :

• tout calcul supplémentaire de ${\pi}$ serait devenu inutile,
• ${\pi}$ serait alors rationnel (ce qui revient à dire que son développement décimal est périodique à partir d'un certain rang.)

Depuis lors

Depuis lors, on recherche une quelconque forme de régularité, statistique ou autre, pour mieux saisir ce nombre. Ces tests interviennent systématiquement après la découverte de nouvelles décimales ; mais, jusqu'à présent, aucune régularité n'est apparue.

Au final, on ne sait pas si ${\pi}$ est ou non aléatoire (c'est-à-dire si ses décimales sont semblables à la succession de chiffres obtenus lors d'un tirage aléatoire "infini" dans l'ensemble {0,1,2,3,4,5,6,7,8,9}).

A défaut de pouvoir faire autre chose, obtenir de nouvelles décimales et faire des tests dessus est mieux que rien.

Participer au mouvement général du progrès mathématique

Faire avancer la recherche

Des progrès mathématiques sont essentiels pour aller plus loin dans la connaissance et le calcul de ${\pi}$. Ainsi, ce nombre est un support de travail, un objet d'étude choisi pour sa richesse, pour le nombre élevé de domaines dans lesquels il intervient.

${\pi}$ n'est donc pas le but, mais un des moyens permettant de faire progresser certains champs des mathématiques et de l'informatique.

La quadrature du cercle

Par exemple, un problème qui a tenu en échec les mathématiciens pendant deux mille ans (en fait, depuis Anaxagore), la quadrature du cercle, a été résolu avec la preuve de la transcendance de ${\pi}$ par Lindemann (fin XIX^ième siècle).

L'algorithmique

Enfin, programmer un ordinateur pour obtenir plus de décimales est une tâche qui demande une compréhension mathématique toujours plus approfondie des objets manipulés.

Cette recherche contribue donc au développement de nouveaux algorithmes de calculs.

Espérer des retombées technologiques

À partir des décimales

Les décimales de ${\pi}$ peuvent servir à fournir des suites aléatoires utiles pour le fonctionnement de certains algorithmes (fondés sur les méthodes de Monte-Carlo, etc.)...mais rien n'assure que $\pi$ est réellement aléatoire.

De plus, le calcul des décimales peut servir à estimer la rapidité, et contrôler le bon fonctionnement des machines : ainsi, on a pu détecter une erreur sur un Cray-2, en 1988.

Enfin, comprendre comment, à partir d'une écriture simple et intelligible de $\pi$ ($\pi$ = 1,11111.... dans une certaine base, voir plus loin), on aboutit à des décimales semblant complètement aléatoires (en base 10) intéresse le monde de la cryptographie.

À partir des méthodes déployées

Pour avancer dans la suite infinie des décimales de ${\pi}$, on doit élaborer de nouvelles machines et découvrir de meilleures formules, de nouveaux algorithmes.

Pour obtenir le milliard de décimales, on a dû améliorer toutes les méthodes d'évaluation des fonctions mathématiques, des opérations élémentaires, etc.

On se rapproche ainsi des puissances de calcul de l'être humain (notre corps effectue des millions de duplications de l'information génétique - trois milliards de lettres - chaque seconde) ce qui impliquera, par exemple, des progrès en intelligence artificielle.

L'insuccès relatif des recherches dans ce domaine est en effet en partie dû aux faibles capacités de calcul de nos machines par rapport à celles des machines biologiques que l'on cherche à imiter.

Pareillement, ces techniques, développées depuis trente ans, ont permis de rendre plus efficaces les algorithmes d'imagerie numérique (images de synthèse, imagerie médicale et compression.)

Ne rien espérer, relever simplement le défi

C'est un défi comme un autre ; il est étrange qu'essayer de battre le record du 100 mètres paraisse naturel, quand cet autre challenge (obtenir de nouvelles décimales de ${\pi}$) doive se justifier : aux mathématiciens seuls on demande "mais à quoi ça sert ?"

Après ce tour d'horizon des retombées attendues de la découverte de nouvelles décimales de $\pi$, nous allons détailler diverses méthodes utilisées pour récolter ces décimales, pour ensuite nous demander si les résultats obtenus permettent d'en déduire leur caractère aléatoire.

Des formules au cours du temps

Le temps de la géométrie

Méthode d'Archimède

De l'Antiquité jusqu'au XVII^ième, les méthodes utilisées sont inspirées d'Archimède de Syracuse (287 - 212 av. J.-C.).

Ce dernier avait établi, dans De la mesure du cercle, que le rapport entre la surface et le carré du rayon d'un cercle est égal au rapport entre son périmètre et son diamètre puis (sans aucune notation algébrique, sans système de numération de position) en considérant des polygones de 6, 12, 24, 48 et 96 côtés, il obtint un encadrement de ce rapport (c'est-à-dire de ${\pi}$)...

$\frac{223}{71} < \pi < \frac{22}{7}$

soit $3,1408 < \pi < 3,1429$.

Ce fut la première méthode permettant de calculer ${\pi}$ avec une précision aussi grande que souhaitée : on encadre un cercle de rayon 1 par deux polygones réguliers (inscrit et circonscrit) de $3 \times 2^n$ côtés, dont on calcule les périmètres.

En notant $a_n$ le demi-périmètre du polygone inscrit, et $b_n$ celui du polygone circonscrit, alors on a $\left\{ \begin{array}{l} a_{1}=2\sqrt{3}, b_{1}=3, \\ \frac{1}{a_{n}}+\frac{1}{b_{n}}=\frac{2}{a_{n+1}},\\ b_{n}a_{n+1}=b_{n+1}^{2} \end{array}\right.$

Travaux pratique

1. Réfléchir à comment obtenir de telles formules à partir des polygones inscrits et exinscrits.
2. Les programmer, pour obtenir $\pi$ avec la précision souhaitée.

Devenir de la méthode d'Archimède

Cette méthode pour calculer ${\pi}$ permet de diviser par 4 l'erreur à chaque étape : on gagne trois décimales en cinq étapes.

Pendant 18 siècles, on utilisa des variantes de cette méthode, comme celle due à François Viète (1540-1603) :

$\pi = 2 \times \frac{2}{\sqrt{2}} \times \frac{2}{\sqrt{2+\sqrt{2}}} \times \frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}} \times ...$

qu'il a obtenu en inscrivant un carré dans un cercle, puis un octogone, etc. Ce fut la première écriture de ${\pi}$ utilisant une infinité de termes.

Les calculs sont délicats, et l'adoption du système décimal s'est fait lentement. C'est pourquoi, durant cette longue période, on n'a jamais atteint la quarantième décimale.

Travaux pratiques

1. Obtenir $\pi$ par la méthode de Viète.
2. Comparer la vitesse de convergence par rapport à la méthode d'Archimède.

Le temps de l'arc tangente et des séries

La formule de Gregory

Développement de l'arc tangente

Le mathématicien écossais James Gregory (1638-1675), qui est l'inventeur du télescope à miroir secondaire, découvrit que $Arctan (x)=x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-\frac{x^{7}}{7}+...$

en considérant, approximativement, que la fonction Arctan est la primitive de

$\frac{1}{1+x^{2}}=1-x^{2}+x^{4}-x^{6}+x^{8}...$

Où $\pi$ réapparaît.

En prenant $x=1$ dans le développement d'arc tangente, on trouve que

$\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}...$

La convergence de cette formule est logarithmique : le nombre d'étapes pour gagner un chiffre supplémentaire devient de plus en plus grand.

Cependant, en prenant un $x$ voisin de 0, on améliore la convergence de la série...

Travaux pratiques

1. Utilisez la formule ci-dessus pour obtenir une approximation de $\pi$.
2. La comparer aux méthodes précédentes.

Développement dans la base de Gregory

Tout nombre réel $x$ s'écrit sous la forme

$x=4(a_{0}-\frac{1}{3}a_{1}+\frac{1}{5}a_{2}-\frac{1}{7}a_{3}+...)$

avec $a_{i}=0$ ou 1, et on peut rendre cette écriture unique (et obtenir ainsi un algorithme de conversion de base) en imposant :

• $a_{2i}=1\Leftrightarrow \sum _{j=0}^{2i-1} \frac{(-1)^j}{2j+1} a_{j}\leqslant \frac{x}{4},$
• $a_{2i+1}=1\Leftrightarrow \sum _{j=0}^{2i} \frac{(-1)^j}{2j+1} a_{j}\geqslant \frac{x}{4},$

Ce développement n'est pas plus absurde que celui en base 10 (les calculs y sont cependant moins élémentaires), et pour ce développement : 0=[0 0 0 0 0 0...] et ${\pi}$ = [1 1 1 1 1 1...].

Sous cet angle, ${\pi}$ est aussi simple que 0.

Utilisation de ce genre de formules

De Gregory à Guilloud et Bouyer, c'est-à-dire de la quarantième à la millionième décimale, du XVII^ième siècle à 1973, ou encore de la main à l'ordinateur, on utilisa des formules d'arc tangente, provenant de l'écriture d'une formule trigonométrique à partir d'un triangle simple :

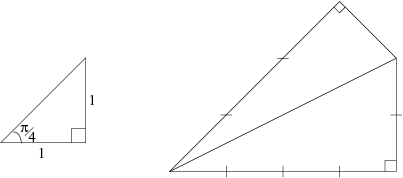
Explications

Figure de gauche : la tangente de $\frac{\pi}{4}$ vaut "le côté opposé sur le côté adjacent" , soit $\frac{\pi}{4} = Arctan \frac{1}{1}$

En procédant de la même manière avec la figure de droite, on trouve $\frac{\pi }{4} = Arctan \frac{1}{2} + Arctan \frac{1}{3}.$

D'autres formules d'arc tangentes

Pour obtenir d'autres formules d'arc tangentes, on peut partir de $\frac{\pi}{4}$ = arctan $\frac{1}{1}$ et utiliser

$ Arctan \left(\frac{1}{n}\right) = Arctan \left(\frac{1}{n+p}\right) + Arctan \left(\frac{p}{n^{2}+\mathit{np}+1}\right)$

pour, en procédant par récurrence, augmenter la convergence des séries associées.

Performance des formules d'arc tangente.

Toutes ces formules sont faiblement convergentes :

• quadratiques en temps ($O(n^2 ln(n))$)
• linéaires en espace (pour obtenir deux fois plus de décimales, il faut quatre fois plus de temps et deux fois plus de mémoire).

Pendant une vingtaine d'années, on utilisa la puissance de calcul des ordinateurs à plein régime, sans vraiment réfléchir. Seulement, pour passer du million au milliard de chiffres, il faut des ordinateurs un million de fois plus puissants, soit vingt doublements de puissance.

Suivant la loi de Moore, la puissance des ordinateurs double tous les 18 mois. De plus, le coût de mise au point des processeurs est multiplié par deux tous les quatre ans : le temps nécessaire pour augmenter la puissance des ordinateurs se rallonge...

Bref, il aurait fallu, à ce rythme, au moins 40 ans avant d'atteindre la milliardième décimale (soit, vers 2010).

Travaux pratiques

1. Utiliser les premiers exemples de formules d'arc tangentes pour obtenir une estimation de $\pi$.
2. Mettre en place le procédé récursif ci-dessus pour générer de nouvelles formules d'arc tangentes.
3. Utiliser les formules que vous obtenez ainsi, pour un calcul plus approfondis de $\pi$.
4. Comparer le tout.

Du million au milliard

Comment passer du million au milliard

Cette milliardième décimale a été trouvée en 1989, par les frères Chudnovsky.

Pour gagner plus de 20 ans, on n'a pas attendu l'amélioration du matériel : les mathématiciens ont cherché de nouvelles formules, et les algorithmes ont été mieux pensés.

De nouveaux algorithmes

Diverses idées sont mises en oeuvre pour gagner en rapidité :

• La méthode de Hörner permet, dans certains cas, de réduire le nombre de multiplications, quand la méthode de Karatsuba, ou l'utilisation de la transformée de Fourier rapide, réalisent ces produits plus rapidement.
• La méthode de Newton permet de calculer un inverse ou d'extraire une racine carrée efficacement.
• Enfin, il existe certaines idées pour accélérer la convergence d'une suite, comme le delta-2 d'Aitken.

De nouvelles formules

De plus, depuis 1975, on ne cherche plus du côté des formules d'arc tangente : on souhaite dorénavant des formules à convergence rapide.

Les idées de ces nouvelles formules sont issues des travaux de Ramanujan, de ses formules étonnantes, comme :

$\pi =\frac{9801}{\sqrt{8}}\left(\sum _{n=0}^{\infty}{\frac(4n)!(1103+26390n){(n!)^{4}396^{4n}}}\right)^{-1}$

ou de ses travaux sur les identités modulaires.

Quand on les combine avec les algorithmes précédents, on peut espérer obtenir $n$ décimales en $O(n ln^4 n)$ opérations élémentaires.

Travaux pratiques

Essayez d'obtenir une approximation de $\pi$ par la formule de Ramanujan. On pourra faire l'inverse par une méthode de type Newton.

Suites de Brent et Salamin

Voici un exemple de suites actuellement utilisées, dues à Brent et Salamin (v. 1975), et basées cette fois-ci sur les travaux de Gauss :

$\left\{ \begin{array}{l}a_{0}=1, b_{0}=\frac{1}{\sqrt{2}}, s_{0}=\frac{1}{2},\\ a_{k}=\frac{a_{k-1}+b_{k-1}}{2},\\ b_{k}=\sqrt{a_{k-1}b_{k-1}},\\ s_{k}=s_{k-1}-2^{k}c_{k},\\ c_{k}=a_{k}^{2}-b_{k}^{2}\end{array}\right.$

Alors $p_{k}=\frac{2a_{k}^{2}}{s_{k}}\rightarrow \pi$ et le nombre de décimales exactes double à chaque itération : avec 25 étapes, on obtient 45 millions de décimales exactes.

On a trouvé des algorithmes d'ordre 9 (neuf fois plus de décimales par étape), et montré qu'il existe de tels algorithmes pour tout ordre...mais il faut un compromis entre ordre et complexité des calculs. Pour cela, l'ordre 4 semble idéal.

Travaux pratiques

Obtenir des décimales de $\pi$ en exploitant les suites de Brent et Salamin.

Conclusion

On sait donc

• additionner en temps linéaire ($O(n)$ opérations élémentaires),
• multiplier en guère plus de temps ($O(n ln(n) ln(ln(n))$),
• et diviser ou extraire des racines sensiblement à la même vitesse.

On ne sait pas si ces algorithmes sont optimaux, mais on ne pourrait guère aller plus vite.

Avec ces nouvelles formules, et ces algorithmes, en doublant la puissance de calcul, on double presque le nombre de décimales exactes, vu que les opérations élémentaires se font en un temps quasi linéaire.

Ces progrès servent aussi au calcul des fonctions trigonométriques et hyperboliques.

Notons qu'en ce qui concerne l'espace mémoire, il n'y a pas grand chose à faire : il faut une taille $n$ pour stocker $n$ décimales, puisqu'à ce jour, aucun schéma ne semble se dessiner dans les mille milliard de décimales calculées.

Quelques méthodes de calcul de $\pi$

La méthode de Newton (1642-1727)

Description de la méthode

La formule

$\frac{\pi}{6} = \frac{1}{2} + \frac{1}{2}\frac{1}{3}\frac{1}{2^3} + \frac{1 \times 3}{2 \times 4}\frac{1}{5}\frac{1}{2^5} + \frac{1 \times 3 \times 5}{2 \times 4 \times 6}\frac{1}{7}\frac{1}{2^7} + ... + \frac{1 \times 3 \times ... \times (2p-1)}{2 \times 4 \times ... \times (2p)}\frac{1}{2p+1}\frac{1}{2^{2p+1}}+...$

Comment Newton la montra

On sait que

$(1+x)^n = 1+nx+\frac{n(n-1)}{2} x^2+...$

Cette formule semble se généraliser à $n \in \mathbb{R}.$ Or, la dérivée de $Arcsin(x)$ est $\frac{1}{\sqrt{1-x^2}}$, qui peut s'écrire sous forme d'une somme infinie avec le développement ci-dessus.

D'où un développement d' $Arcsin(x)$ (par primitivation) : $Arcsin(x) = x + \frac{1}{2}\frac{x^3}{3} + \frac{1 \times 3}{2 \times 4}\frac{x^5}{5} + ...$

et, en prenant $x=\frac{1}{2}$, on trouve la formule énoncée.

Sa convergence

On gagne 3 chiffres en 5 étapes, comme dans la méthode d'Archimède. Newton utilisa une formule analogue pour trouver 16 décimales de $\pi$.

Travaux pratiques

1. Utilisez cette formule pour obtenir des décimales de $\pi$.
2. Vérifiez, en utilisant d'autres méthodes de calcul de $\pi$, que l'on gagne bien 3 chiffres en 5 étapes.
3. Regardez s'il n'y a pas moyen, en utilisant les méthodes présentées ici, de gagner en rapidité de convergence.

La méthode de Kreweras

Présentation de la méthode

Cette méthode, proposée par G. Kreweras en 1980, permet de calculer $\pi$ avec une seule multiplication, une seule division, et des additions.

On remplit le tableau suivant ligne par ligne, en fixant un nombre maximal de lignes et de colonnes, correspondant à notre désir de précision.

Pour trouver la valeur de l'élément $e_{i,j}$, on calcule la somme des j derniers éléments de la ligne i-1 (par exemple, 224, en position (7,4), est bien la somme des 4 derniers éléments de la ligne 6)...

Le tableau

	0	1	2	3	4	5	6	7	8	9
0	1
1	0	1
2	0	1	1
3	0	1	2	2
4	0	2	4	5	5
5	0	5	10	14	16	16
6	0	16	32	46	56	61	61
7	0	61	122	178	224	256	272	272
8	0	272	544	800	1024	1202	1324	1385	1385
9	0	1385	2770	4094	5296	6320	7120	7664	7936	7936

Le résultat

On peut démontrer que $\pi = \lim_{n \rightarrow +\infty} \frac{2 n e_{n-1,n-1}}{e_{n,n}}$

Les premières approximations sont 2. 4. 3. 3,2. 3,125. 3,147. 3,1397. 3,1422. 3,1413. etc.

Les $e_{n,n}$ sont les nombres d'Euler : le nombre de façons de classer les entiers de 1 à n en zigzag :

• $e_{3,3}=2$ car : 1 3 2, 2 3 1 sont les deux seules manières de ranger ces trois nombres en zigzag,
• $e_{4,4}=5$ car : 1 4 2 3, 2 4 1 3, 1 3 2 4, 2 3 1 4, 3 4 1 2.

Travaux pratiques

• Obtenir des approximations de $\pi$ par cette méthode,
• Obtenir le n^ième nombre d'Euler.

La méthode de Monte-Carlo (appliquée au calcul de $\pi$)

La méthode

On tire aléatoirement deux réels x et y dans [-1;1], et l'on regarde si le point de coordonnées (x,y) appartient au cercle de centre 0, rayon 1 (c'est-à-dire si $x^2+y^2=1$).

Si c'est le cas, on incrémente notre compteur. Alors le rapport

$\frac{\textrm{compteur}}{\textrm{nombre total de tirages}}$

tend vers $\frac{\pi}{4}$ (quotient de la surface du carré par celle du disque).

À propos de la convergence

La convergence est trés lente, et n'est réellement assurée que si l'on a du vrai aléatoire.

Travaux pratiques

• Mettre en oeuvre cette méthode pour obtenir une approximation de $\pi$.
• Représenter graphiquement les tirages.

$\pi$ est-il aléatoire ?

Les résultats actuels

L'état de l'art

Parmi les divers tests effectués, on trouve par exemple le calcul de la fréquence des 10 chiffres, des 100 paires de chiffres, le calcul de diverses moyennes, etc.

A chaque fois, le même constat : les décimales de ${\pi}$ ressemblent à une succession de chiffres tirés aléatoirement.

Travaux pratiques

Faire ces tests sur vos obtentions de $\pi$.

${\pi}$ serait donc aléatoire ?

${\pi}$ n'est pas un nombre choisi au hasard, mais est parfaitement déterminé et exceptionnel, riche de diverses définitions et propriétés. De plus, dans certains systèmes de représentation, l'écriture de ${\pi}$ n'est pas quelconque, donc ${\pi}$ n'est pas intrinsèquement aléatoire.

La transcendance de ${\pi}$ n'empêche nullement toutes sortes de régularités (n'avoir plus que des 5 et des 6 à partir d'un certain rang, par exemple).

Cependant, il a été prouvé que certaines répétitions trop longues sont interdites à partir d'un certain rang (comme avoir $15n$ zéros à partir du rang $n$).

Est-ce si étonnant ?

Quel aléas ?

Peut-être ne doit-on pas tant s'étonner de l'apparence aléatoire de ses décimales : la définition de ce nombre est sans rapport avec la base 10.

Par contre, chaque formule faisant intervenir ${\pi}$ peut être interprétée comme un développement régulier de ${\pi}$. Ainsi, ${\pi}$ s'écrit 2,222222... dans la base à pas variable $\left[ \frac{1}{3},\frac{2}{5},\frac{3}{7},... \right]$ puisque l'on a $\pi =2 \left(1+\frac{1}{3}+\frac{1\mathrm{x}2}{3\mathrm{x}5}+\frac{1\mathrm{x} 2 \mathrm{x}3}{3\mathrm{x} 5 \mathrm{x}7}+...\right)$

Démonstration

Euler obtint cette égalité à partir d'un développement de la fonction arc tangente, provenant de la résolution de l'équation différentielle $2z'(y-y^{2})+z(1-2y)=1,$ où $y(x)=\frac{x^{2}}{1+x^{2}},z(x)=\frac(1+x^{2}) Arctan (x){x}.$

Discussion

Au final, ce qui est surprenant, c'est que ${\pi}$ se comporte comme un nombre aléatoire : cela demande à être vérifié et expliqué !

Se peut-il qu'un changement de base (donc des opérations arithmétiques élémentaires) engendre le hasard ? Si tel est le cas, cela pourrait grandement intéresser les cryptologues.

Peut-être n'en sait-on pas assez sur la notion d'aléatoire ?

Sur l'assurance en mathématiques

Si beaucoup pensent, suite à ces échecs, que ${\pi}$ est aléatoire, il faut se souvenir que :

1. avant 1995, la communauté scientifique était convaincue que pour obtenir la n+1^ième décimale de ${\pi}$, il fallait connaître les n décimales qui la précédaient. Simon Plouffe a prouvé que cela n'était pas nécessaire.
2. dans le même esprit, on a récemment trouvé une formule générant tous les nombres premiers, dans l'ordre. Avant cette découverte, les mathématiciens étaient généralement convaincus qu'une telle formule n'existait pas.

Lien entre aléatoire et déterminé

Peut-être que ces recherches permettront, un jour, de mieux saisir le lien entre aléatoire et pleinement déterminé.

Cela faciliterait la génération de nombres aléatoires, et aiderait à mieux comprendre certaines structures régulières rencontrées dans la nature (les côtes bretonnes, les nuages... tiennent à la fois des structures fractales ordonnées, et de l'aléatoire).