---

Des automates différents peuvent être associés au même langage.

L'optimisation des programmes d'analyse syntaxique (dont certains sont des réalisations concrètes d'automates finis) rend nécessaire la construction d'un automate minimal (en nombre d'états) qui reconnaissent un langage donné.

On se limitera dans ce chapitre à la simplification d'un automate de Moore (puisque la méthode de construction par sous-ensemble permet de se ramener d'un AFND à un AFD).

Congruences d'automates

Soit $(E,I,t)$ un AFD et $\mathcal{R}$ une relation d'équivalence sur $E$.

Quelques rappels

On rappelle que $\mathcal{R}$ est une relation binaire sur l'ensemble $E$ des états, qui a en plus les propriétés suivantes...

Réfléxivité

Pour tout état $e \in E, ~ e \mathcal{R} e$,

Symétrie

Pour tout couple d'états $(e_1, e_2) \in E^2$ si $e_1 \mathcal{R} e_2$, alors $e_2 \mathcal{R} e_1$,

Transitivité

Pour tout triplet d'états $(e_1, e_2, e_3) \in E^3$ si $e_1 \mathcal{R} e_2$ et $e_2 \mathcal{R} e_3$, alors $e_1 \mathcal{R} e_3$.

---

Exercice : On considère l'automate :

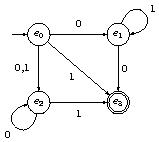
et la relation binaire $e_i \mathcal{R} e_j$ si et seulement si $i$ et $j$ ont la même parité.

Montrez que $\mathcal{R}$ est bien une relation d'équivalence sur $E$.

---

On rappelle encore que $t : E \times I \rightarrow E$ est la fonction de transition. Par la suite, par souci de concision, on notera $t_{x}(e)$ pour $t(e,x)$.

Définition

---

Définition (Congruence d'automates)

On dit que $\mathcal{R}$ est une congruence d'automates si et seulement si $\forall (r,s) \in E^2, \forall x \in I, (r \mathcal{R} s) \Longrightarrow (t_x(r) \mathcal{R} t_x(s))$ C'est-à-dire si toute paire d'états équivalents modulo $\mathcal{R}$ est transformée par toute entrée en une paire d'états équivalents modulo $\mathcal{R}$.

---

---

Exercice : La relation d'équivalence $\mathcal{R}$ de l'exercice précédent est-elle une congruence d'automates ?

---

Ensemble quotient

Soit $\mathcal{R}$ une congruence d'automates sur l'AFD $(E,I,t)$.

Notation: On note $\tilde{E}$, l'ensemble quotient $E/\mathcal{R}$.

---

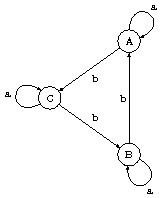
Exercice : Représenter le graphe de l'automate $M$ dont la table de transition des états est

$t $	$ a $	$ b $
$e_0 $	$ e_0 $	$ e_4$
$e_1 $	$ e_1 $	$ e_0 $
$e_2 $	$ e_2 $	$ e_4 $
$e_3 $	$ e_5 $	$ e_2 $
$e_4 $	$ e_4 $	$ e_3 $
$e_5 $	$ e_3 $	$ e_2 $

Soit $\mathcal{R}$ la relation d'équivalence pour laquelle $E/ \mathcal{R} = \{ \{ e_0, e_2 \}, \{ e_1, e_3, e_5 \}, \{ e_4 \} \}.$

1. Donner la table de transition d'états de l'automate-quotient.
2. Représenter son graphe

---

Réponses :

$E $	$ a $	$ b$
$A = \{e_0, e_2\} $	$ \{e_0, e_2\} $	$ \{e_4\} $
$B = \{e_1, e_3, e_5 \} $	$ \{e_1, e_3, e_5 \} $	$ \{e_0, e_2\}$
$C = \{e_4\} $	$ \{e_4\} $	$ \{e_1, e_3, e_5 \} $

---

Exercice : Soit $M$ l'automate fini dont la table de transition des états est

$t $	$ 0 $	$ 1 $
$1 $	$ 1 $	$ 4 $
$2 $	$ 3 $	$ 5 $
$3 $	$ 2 $	$ 5 $
$4 $	$ 4 $	$ 1 $
$5 $	$ 3 $	$ 4 $

Soit $\mathcal{R}$ la relation d'équivalence sur $E = \{1,2,3,4,5\}$ telle que $1 \mathcal{R} 4$ et $3 \mathcal{R} 2$.

1. Que vaut $E/\mathcal{R}$?
2. Montrer que $\mathcal{R}$ est une congruence d'automates.
3. Donner la table de transition des états de l'automate-quotient.
4. Représenter son graphe.

---

---

Exercice : Soit $M$ l'automate fini dont le graphe est représenté par la figure

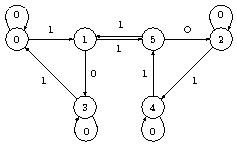
Le tableau ci-dessous figure une relation binaire $\mathcal{R}$ dans l'ensemble des états $E = \{ 0,1,2,3,4,5 \}$ :

$	$ 0 $	$ 1 $	$ 2 $	$ 3 $	$ 4 $	$ 5 $
$0 $	$ 1 $	$ 0 $	$ 0 $	$ 0 $	$ 1 $	$ 0 $
$1 $	$ 0 $	$ 1 $	$ 0 $	$ 0 $	$ 0 $	$ 1 $
$2 $	$ 0 $	$ 0 $	$ 1 $	$ 1 $	$ 0 $	$ 0 $
$3 $	$ 0 $	$ 0 $	$ 1 $	$ 1 $	$ 0 $	$ 0 $
$4 $	$ 1 $	$ 0 $	$ 0 $	$ 0 $	$ 1 $	$ 0 $
$5 $	$ 0 $	$ 1 $	$ 0 $	$ 0 $	$ 0 $	$ 1 $

Un chiffre 1 à l'intersection de la ligne $i$ et de la colonne $j$ signifie que $i \mathcal{R} j$, et un chiffre 0 que ces deux éléments ne sont pas en relation.

1. Montrer que $\mathcal{R}$ est une relation d'équivalence sur $E$.
2. Montrer que $\mathcal{R}$ est une congruence d'automates.
3. Représenter le graphe de l'automate-quotient $M/\mathcal{R}$.

---

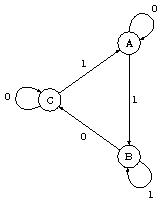
Réponses :

$E $	$ 0 $	$ 1 $
$A = \{0, 4 \} $	$ \{0, 4 \} $	$ \{1, 5\} $
$B = \{1, 5\} $	$ \{3, 2\} $	$ \{1, 5\} $
$C = \{3, 2\} $	$ \{3, 2\} $	$ \{0, 4 \}$

Remarque : On peut définir une application $\tilde{t}_x : \tilde{E} \rightarrow \tilde{E}$ par $\tilde{t}_x (\dot{e}) = \dot{[t_x(e)]}$, puis une application $\tilde{t} : \tilde{E} \times I \rightarrow \tilde{E}$ par $(\dot{e},i) \longmapsto \tilde{t}_x(\dot{e})$.

Équivalence de Nérode

L'équivalence

Soit $M = (E,I,t,e_0,A)$ un automate de Moore, deux états $q$ et $s$ de $E$, et $w \in I^*$ un mot d'entrée.

---

Définition (w-compatibles)

$q$ est $s$ sont $w$-compatible si et seulement si $t_w(q) \in A \Longleftrightarrow t_w(s) \in A$

---

Cette définition permet de définir une relation $\sim$ dans $E$ par

$(q \sim s) \Longleftrightarrow \left(\forall w \in I^*, q \textrm{ et } s \textrm{ sont } w \textrm{-compatibles} \right)$

---

Définition (Équivalence de Nérode)

Cette relation est manifestement une relation d'équivalence, elle est appelée équivalence de Nérode associée à $M$.

---

On démontre facilement que cette équivalence est une congruence d'automates. Tout automate de Moore peut donc être remplacé par son quotient par l'équivalence de Nérode.

Dans ce quotient, le nombre d'états est évidemment plus petit, l'automate obtenu est donc plus « simple».

L'algorithme

La théorie

Pour obtenir l'équivalence de Nérode associée à un automate, on dispose de l'algorithme suivant...

Soit $M=\{E,I,t,e_0,A\}$ un automate de Moore.

On définit, pour tout $k \in \mathbb{N}$, une relation $\mathcal{R}_k$ sur E en posant

[$q \mathcal{R}_k s $] $\Longleftrightarrow$ $(\forall w \in I^*), (l(w) \leqslant k \Longrightarrow q$ et $s$ sont $w$-compatibles)

Donc $q$ et $s$ sont en relation par $\mathcal{R}_k$ lorsqu'ils sont $w$-compatibles, pour tout mot $w$ de longueur inférieure ou égale à $k$.

Cette relation est clairement une relation d'équivalence, et $\mathcal{R}_{k+1}$ est plus fine que $\mathcal{R}_k$. L'équivalence de Nérode est l'intersection de ces relations $\mathcal{R}_k$, pour toutes les valeurs de $k$ entier.

La pratique

Cet algorithme n'est pas utilisable dans la pratique. On fait plutôt...

• Prendre comme partition de départ $P_0 = \{A, E \setminus A \}$.
• Si $P_k=\{E_1, , E_n \} $ est la partition correspondant à la relation $\mathcal{R}_k$, morceler éventuellement chaque classe $E_i$ en sous-classes $E_{i1}, E_{i2}, , E_{ip}$ de manière que deux états $q$ et $s$ appartiennent à la même sous-classe si, pour toute entrée $x$, les états $t_x(q)$ et $t_x(s)$ appartiennent à la même classe $E_j$ (pouvant dépendre de $x$).

• Répéter l'étape précédente jusqu'à ce que $P_{k+1}=P_k$. La relation $\mathcal{R}_k$ est alors l'équivalence de Nérode associée à M.

Remarque : L'étape (3) est nécessairement atteinte, puisque les relations $\mathcal{R}_k$ sont de plus en plus fines.

Au pire, $P = \{ \{q \} \|q \in E \}$, la relation est l'égalité : ceci signifie que l'automate n'est pas simplifiable.

---

Exemple : Un automate de Moore et l'automate simplifié.

---

---

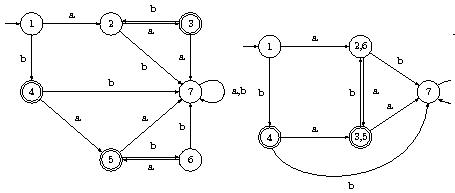
Exercice : On donne un AFD par la table de transition des états suivante :

$t $	$ a $	$ b$
$0 $	$ 1 $	$ 2 $
$1 $	$ 5 $	$ 3 $
$2 $	$ 5 $	$ 1 $
$3 $	$ 4 $	$ 5 $
$4 $	$ 5 $	$ 4 $
$5 $	$ 5 $	$ 5 $

État initial : 0

États d'acceptation : 4

Cet automate reconnaît le langage défini par l'expression régulière $(a|bb)bab^*$.

Appliquer la méthode de l'équivalence de Nérode pour trouver l'automate minimal reconnaissant le langage.

---

---

Exercice : Faire de même avec l'automate de Moore dont la table de transition est :

$t $	$ a $	$ b$
$a $	$ a $	$ c $
$b $	$ g $	$ d $
$c $	$ f $	$ e $
$d $	$ a $	$ d $
$e $	$ a $	$ d $
$f $	$ g $	$ f $
$g $	$ g $	$ c $

---

Méthode du dual

Dual d'un automate

Soit $M = (E,I,t,S,A)$ un automate quelconque (AFD ou AFND).

---

Définition (Automate dual)

L'automate dual de $M$ est l'automate $M^{-1} = (E,I,t',A,S)$, où $t'$ est la relation sur $E$ obtenue en renversant toutes les flèches sur le graphe de $M$.

C'est-à-dire, si $R' \subset (E \times I) \times E$ est le graphe de la relation $t'$, alors que le graphe de $t$ est $R$, on a $((e,i),e') \in R' \Longleftrightarrow ((e',i),e) \in R$

---

Il est clair que $M$ reconnaît un mot $w \in I^*$ si et seulement si $M^{-1}$ reconnaît le mot $w^{-1}$ (si $w = a_1 a_2 a_n$, alors $w^{-1} = a_n a_{n-1} a_1$).

Le dual d'un automate à comportement déterminé n'est pas nécessairement à comportement déterminé.

Méthode du dual

Soit $M$ un automate de Moore :

1. Construire l'automate dual $M^{-1}$ de $M$.
2. Appliquer la construction par sous-ensembles à $M^{-1}$ pour le transformer en automate $M'$ de Moore.
3. Construire le dual ${M'}^{-1}$ de $M'$.
4. Appliquer la construction par sous-ensemble à ${M'}^{-1}$ pour obtenir l'automate de Moore $M''$.

L'automate $M$ est l'automate minimal tel que $\mathcal{L}(M) = \mathcal{L}(M)$.

---

Exercice : On donne un AFD par la table de transition des états suivante :

$t $	$ a $	$ b$
$0 $	$ 1 $	$ 2 $
$1 $	$ 3 $	$ 4 $
$2 $	$ 3 $	$ 4 $
$3 $	$ 5 $	$ 6 $
$4 $	$ 5 $	$ 6 $
$5 $	$ 7 $	$ 8 $
$6 $	$ 7 $	$ 8 $
$7 $	$ 9 $	$ 10 $
$8 $	$ 9 $	$ 10 $
$9 $	$ 11 $	$ 12 $
$10 $	$ 11 $	$ 12 $
$11 $	$ 1 $	$ 2 $
$12 $	$ 1 $	$ 2 $

État initial : 0

États d'acceptation : 0 3 4 5 6 7 8 11 12

Cet automate reconnaît le langage défini par l'expression régulière $((a|b)^2)^* | ((a|b)^3)^*$.

Appliquer la méthode du dual pour trouver l'automate minimal reconnaissant le langage.

---

---

Exercice : On donne un automate non déterministe, à transitions instantannées, par la table de transition suivante :

$t $	$ \varepsilon $	$ a $	$ b$
$0 $	$ 1,11 $	$ $	$ $
$1 $	$ 2, 7 $	$ $	$ $
$2 $	$ $	$ $	$ 3 $
$3 $	$ 4, 6 $	$ $	$ $
$4 $	$ $	$ 5 $	$ $
$5 $	$ 4, 6 $	$ $	$ $
$6 $	$ 10 $	$ $	$ $
$7 $	$ $	$ 8 $	$ $
$8 $	$ $	$ $	$ 9 $
$9 $	$ 10 $	$ $	$ $
$10 $	$ 22 $	$ $	$ $
$11 $	$ 12,14 $	$ $	$ $
$12 $	$ $	$ 13 $	$ $
$13 $	$ $	$ $	$ $
$14 $	$ 17 $	$ $	$ 15 $
$15 $	$ $	$ $	$ 16 $
$16 $	$ 17 $	$ $	$ $
$17 $	$ $	$ 18 $	$ $
$18 $	$ 19,21 $	$ $	$ $
$19 $	$ $	$ $	$ 20 $
$20 $	$ 19,21 $	$ $	$ $
$21 $	$ 22 $	$ $	$ $
$22 $	$ $	$ $	$ $

État initial : 0

État d'acceptation : 22

Cet automate reconnaît le langage défini par l'expression régulière $ba^* | ab | (a | bb) ab^*$.

Le déterminiser, puis lui appliquer la méthode de votre choix pour obtenir l'automate minimal reconnaissant le langage.

---

---

Exercice : On donne la table de transition suivante pour un automate fini :

$t $	$ a $	$ b $
$0 $	$ 1 $	$ 2 $
$1 $	$ 3 $	$ 4 $
$2 $	$ 5 $	$ 6 $
$3 $	$ 1 $	$ 2 $
$4 $	$ 7 $	$ 8 $
$5 $	$ 7 $	$ 8 $
$6 $	$ 1 $	$ 2 $
$7 $	$ 9 $	$ 10 $
$8 $	$ 10 $	$ 11 $
$9 $	$ 7 $	$ 8 $
$10 $	$ 10 $	$ 10 $
$11 $	$ 7 $	$ 8 $

L'état initial est 0, et les états d'acceptation sont 4, 5, 9 et 11.

Appliquer à cet automate l'algorithme de votre choix pour obtenir l'automate minimal reconnaissant le même langage (équivalence de Nérode ou dual).

(L'automate minimal possède 7 états).

---

Synthèse

Outils

Construction par sous-ensemble

Domaine d'application

Cette méthode s'applique aux automates finis non déterministes. Il est aussi possible de l'utiliser sur un AFD, mais c'est sans intérêt.

Résultat

Automate reconnaissant le même langage.

But

Obtenir un AFD reconnaissant le même langage.

Autre utilisation

Peut permettre d'obtenir l'automate minimal reconnaissant le même langage (méthode du dual).

Équivalence de Nérode

Domaine d'application

Cette méthode ne s'applique qu'aux automates finis déterministes (AFD).

Résultat

Le quotient de l'automate considéré par l'équivalence de Nérode ; un automate ne reconnaissant généralement pas le même langage.

But

Simplifier l'automate considéré, si c'est possible, grâce à la méthode des quotients.

Méthodes d'optimisation

Méthode des quotients

Domaine d'application

Cette méthode ne s'applique qu'aux automates finis déterministes (AFD).

Moyens

Équivalence de Nérode.

Résultat

On obtient l'automate minimal reconnaissant le même langage.

Méthode du dual

Domaine d'application

Cette méthode ne s'applique qu'aux automates finis déterministes (AFD).

Moyens

Construction par sous-ensembles.

Résultat

L'automate de Moore minimal reconnaissant le même langage.

Efficacité

Élégant, mais pas efficace.