La divisibilité des entiers

Divisibilité par 2, 5 et 10

Présentation

Un nombre est divisible par 2 si, et seulement s'il a pour dernier chiffre 0, 2, 4, 6 ou 8. Il est divisible par 5 ssi il se termine par 0 ou 5. Enfin, il est divisible par 10 si, et seulement s'il se termine par 0.

Cela se généralise :

• Un nombre est divisible par 4 si et seulement si le nombre constitué par ses 2 derniers chiffres l'est. Il l'est par $2^n$ si et seulement si le nombre de ses $n$ derniers chiffres l'est.
• De même, un nombre est divisible par $5^n$ (resp. $10^n$) ssi le nombre constitué de ses $n$ derniers chiffres l'est.

Travaux pratiques

Écrire en python (sans utiliser le modulo) un code pour tester respectivement la divisibilité par 2, 5 et 10. Réfléchir à la généralisation.

Divisibilité par 3 et 9

Présentation

Un nombre est divisible par 3 si la somme de ses chiffres l'est. Par exemple, pour l'entier 12345, la somme vaut 1+2+3+4+5 = 15, qui est divisible par 3, donc 12345 l'est.

• On peut recommencer récursivement sur le résultat de la somme, au besoin.
• Remplacer 3 par 9 dans ce qui précède marche aussi.

Travaux pratiques

Mettre en place un code qui teste ceci.

Divisibilité par 11

Présentation

Un nombre est divisible par 11 si la somme alternée de ses chiffres l'est. Par exemple, pour l'entier 12345, la somme alternée vaut 1-2+3-4+5 = 3, qui n'est pas divisible par 11, donc 12345 ne l'est pas.

Travaux pratiques

Mettre en place ceci. Faire un code final qui teste l'ensemble des divisibilités évoquées ci-dessus.

Les nombres narcissiques

Présentation

Un nombre narcissique est un nombre égal à la somme de ses n chiffres, chacun élevé à la puissance n. Par exemple :

• $153 = 1^3 + 5^3 + 3^3$.
• $1634 = 1^4 + 6^4 + 3^4 + 4^4$.

Il existe 88 nombres narcissiques, le plus grand ayant 39 chiffres.

Travaux pratiques

1. Créez une fonction testant si le nombre passé en argument est narcissique solution.
2. Dressez la liste de tous les nombres narcissiques inférieurs à une valeur donnée.

Les nombres amicaux

Présentation

Deux entiers m et n sont dits amicaux si la somme des diviseurs de m vaut n (m exclu), et si la somme des diviseurs de n vaut m (n exclu).

Les pythagoriciens connaissaient ces nombres. Par exemple,

• Les diviseurs de 220 sont 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 et leur somme vaut 284
• Les diviseurs de 284 sont 1, 2, 4, 71, 142 et leur somme vaut 220.

Quelques couples de nombres amicaux

Voici les premiers nombres amicaux :

• 220 et 284,
• 1184 et 1210,
• 2620 et 2924,
• 5020 et 5564.

On en connaît plus de 7000. On ne sait pas s’ils sont infinis, ni s’il existe deux nombres amicaux premiers entre eux.

Travaux pratiques

1. Testez si deux nombres saisis par l’utilisateur sont amicaux. solution
2. Regarder si ces deux nombres sont premiers entre eux.
3. Trouver l’ami potentiel d’un nombre donné, et tester si ces nombres sont réellement amicaux.
4. Construire la liste exhaustive des nombres amicaux inférieurs à un nombre donné.

On fera, le plus possible, intervenir des fonctions.

Les nombres de Kaprekar

Un nombre de kaprekar (dans une base donnée) est un nombre qui, lorsqu’il est élevé au carré, peut être séparé en une partie gauche et une partie droite telles que leur somme redonne le nombre initial

• Par exemple, $703^2 = 494209$, et $494+209 = 703$.
• Il en va de même pour : 1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 7272, 7777, 9999...
• Tout nombre uniquement constitué de 9 est de Kaprekar.

Dans la version forte de cette définition, on souhaite que les deux parties (gauche et droite) considérées pour la somme aient le même nombre de chiffres (à un près). Il en existe une version plus souple.

Propriétés des nombres de Kaprekar

Les nombres de Kaprekar en base deux coïncident avec les nombres parfaits pairs (voir plus loin).

Si on élève au carré une permutation cyclique d’un nombre de kaprekar, et qu’on additionne les moitiés, on obtient une permutation cyclique du nombre de départ. Par exemple,

• Pour le nombre de kaprekar $7272$, $2727^2 = 7436529$, et $743+6529=7272$.
• Pour le nombre de kaprekar 297, $972^2 = 944784$, et $944+784=1728$. Enfin, 1+728=729 : permutation du nombre de kaprekar de départ.

On peut généraliser cette notion : 297 est aussi un kaprekar triple, puisque $297^3 = 026198073$, et $026+198+073=297$.

Travaux pratiques

1. Testez si l’entier saisi par l’utilisateur est un nombre de Kaprekar. On prendra garde au fait que le nombre peut avoir un nombre impair de chiffres.
2. Obtenez la liste des nombres de kaprekar inférieurs à un entier donné.
3. Généralisez les deux points précédents aux nombres de kaprekar triples, quadruples, etc.
4. Précisez si on a affaire à un nombre de Kaprekar parfait (les deux sous-parties du nombre ont le même nombre de chiffres, à un près), ou pas.

Les nombres polygonaux

Nombres polygonaux et suites arithmétiques

Ce sont les sommes de termes en progression arithmétique :

• raison 1 pour les nombres triangulaires : $T_n = \frac{n (n + 1)}{2}$,

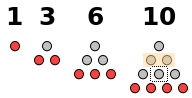
• raison 2 pour les nombres carrés : $C_n = \frac{n (2n + 0)}{2}$,

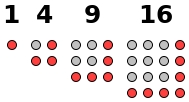
• raison 3 pour les nombres pentagonaux : $P_n = \frac{n (3n - 1)}{2}$,
• raison 4 pour les nombres hexagonaux : $Hx_n = \frac{n (4n - 2)}{2}$,

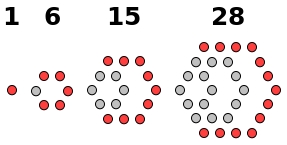
• raison 5 pour les nombres heptagonaux : $Hp_n = \frac{n (5n - 3)}{2}$,
• etc.

Sommes de nombres polygonaux

Tout entier est la somme :

• d’au plus trois nombres triangulaires,
• d’au plus quatre nombres carrés,
• d’au plus cinq nombres pentagonaux,
• etc.

Travaux pratiques

1. Testez si l’entier saisi par l’utilisateur est un nombre polygonal.
2. Dressez la liste des nombres n-gonaux.
3. Cherchez, pour un nombre donné, sa décomposition en nombres triangulaires, carrés, etc.
4. Faites une représentation graphique des nombres n-gonaux.

Les nombres parfaits

Présentation

Un nombre parfait est un nombre égal à la somme de ses diviseurs excepté lui-même (on dit qu’il est la somme de ses parties aliquotes)

• 6 = 1+2+3,
• 28 = 1+2+4+7+14,
• 496 = 1+2+4+8+16+31+62+124+248,
• 8128 = ...

On n’en connaît qu’une quarantaine. Leur infinité est conjecturée.

Propriétés

On a démontré, depuis l’antiquité, diverses propriétés de ces nombres :

1. Ils se terminent -aléatoirement- par 6 ou 28, lorsqu’ils sont pairs. On ne pense pas qu’il existe des nombres parfaits impairs.
2. Euclide (IIIe s. av. J.-C.) prouva que si $2^p-1$ est premier, alors 2p−1 (2p − 1) = 2p−1 Mp est parfait.
3. Euler (XVIIIe s.) a montré que tout nombre parfait pair est de cette précédente forme : ces derniers sont donc reliés aux nombres premiers de Mersenne (les $M_p$).
4. L’ensemble des nombres parfaits pairs coïncident avec l’ensemble des nombres de Kaprekar en base 2.
5. Les nombres parfaits pairs sont triangulaires :
   • 6 = 1 + 2 + 3,
   • 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7,
   • 496 = 1 + 2 + 3 + 4 + . . . + 30 + 31,
   • etc.

1. Enfin, à l’exception de 6, les nombres parfaits pairs :
   • sont sommes de cubes de nombres impairs consécutifs :
     • 28 = 13 + 33,
     • 496 = 13 + 33 + 53 + 73 ,
     • 8128 = 13 + 33 + 53 + . . . + 153 ,
     • etc.
   • ont une racine numérique égale à 1 :
     • pour 28 : 2+8 = 10, 1+0 = 1,
     • pour 496 : 4+9+6 = 19, 1+9 = 10, 1+0=1,
     • pour 8128 : 8+1+2+8 = 19, 1+9 = 10, 1+0 = 1,
     • etc.

Travaux pratiques

1. Testez si l’entier saisi par l’utilisateur est un nombre parfait.
2. Obtenez la liste des nombres parfaits inférieurs à un entier donné.

1. Obtenez des nombres parfaits à partir de nombres premiers de Mersenne.
2. Vérifiez que les nombres parfaits pairs sont triangulaires, et hexagonaux.
3. Vérifiez que les nombres parfaits sont sommes de cubes de nombres impairs consécutifs.
4. Assurez-vous que la racine numérique d’un nombre parfait est égale à 1.
5. Vérifiez le lien entre les nombres parfaits et les nombres de Kaprekar.