WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Methodes De Calcul
On explique ici comment effectuer efficacement un produit, une extraction de racine carrée, ou comment rechercher les zéros d'une fonction, etc.
Des méthodes de calcul au fil du temps
Au temps des égyptiens
Le Papyrus Rhind
Le Papyrus Rhind aurait été écrit, durant la seconde période, par le scribe Ahmès.
Son nom vient de l'Ecossais Henry Rhind, qui l'acheta en 1858 à Louxor. Il (le papyrus) aurait été découvert sur le site de la ville de Thèbes.
Actuellement conservé au British Museum, il contient 87 problèmes résolus d'arithmétique, d'algèbre, de géométrie et d'arpentage.
On y trouve l'approximation 3,1604 pour $\pi$.
Ce papyrus est, en partie, une copie de résultats plus ancien (vers -2000 av. J.-C.) remontant aux babyloniens.
Nous avons déjà étudié une célébrité du papyrus : les fractions égyptiennes. On présente dans ce qui suit la multiplication égyptienne.
La multiplication égyptienne
Son histoire
Elle est présente dans le Papyrus Rhind.
Elle a été redécouverte à la fin du XXe s. par des constructeurs de puissants ordinateurs scientifiques, qui s'y prennent ainsi pour effectuer très rapidement les grandes multiplication.
La méthode
Par exemple, pour effectuer 44*53, on écrit dans une première colonne les puissances de 2 inférieures à 44, et dans une deuxième colonne on part de 53, que l'on double autant de fois que nécessaire :
| 1 | 53 |
| 2 | 106 |
| 4 | 212 |
| 8 | 424 |
| 16 | 848 |
| 32 | 1696 |
Enfin, on supprime les lignes commençant par des nombres n'intervenant pas dans la décomposition de 44 en base 2 : 44=4+8+32, ...donc
| 4 | 212 |
| 8 | 424 |
| 32 | 1696 |
| 44 | 2332 |
Et on a alors le résultat : 44*53 = 2332.
L'explication est immédiate : $44*53 =(2^2+2^3+2^5)*53= 2^2*53+2^3*53+2^5*53 =...$
Intérêt de la méthode
Si on sait faire des additions et des doublements (immédiat en base 2, dans laquelle travaille un ordinateur), alors on sait faire une multiplication par la méthode égyptienne.
Cette méthode est particulièrement efficace.
La méthode de Newton
On rappelle une méthode vue dans un précédent TP.
Présentation de la méthode
La méthode de Newton, proposée par ce dernier vers 1669, permet -entre autre- d'effectuer des inverses et d'extraire des racines en n'effectuant que des produits.
Soit f une fonction suffisamment régulière (par exemple deux fois continûment dérivable), et telle qu'il existe un point a vérifiant :
$f(a)=0~~et~~f'(a) \neq 0$
Alors, en partant d'un $x_0$ pas trop loin de $a$, et en calculant $x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$ on construit une suite qui converge quadratiquement vers $a$ (chaque itération double le nombre de décimales exactes.)
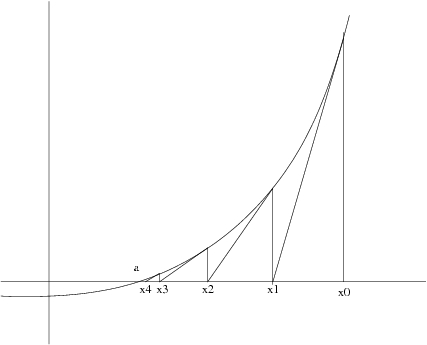
On suit à chaque fois les tangentes
Cette méthode est stable numériquement : la convergence n'est pas génée par de petites erreurs de calcul.
Cas de l'inverse
Pour l'inverse, on prend $f(x) = \frac{1}{x} - b, a = \frac{1}{b}$, et
$x_{n+1} = 2 x_n - b x_n^2$
On a bien convergence quadratique :
$x_{n+1}-\frac{1}{b} = -b \left(x_n - \frac{1}{b} \right)^2$
...et, par cette méthode, le calcul d'un inverse est à peine cinq fois plus coûteux qu'une multiplication.
Cas de la racine carrée
Pour la racine carrée, $f(x) = x^2 - b$, et
$x_{n+1} = \frac{1}{2} \left( x_k + \frac{b}{x_k} \right)$
...méthode environ sept fois plus coûteuse qu'une multiplication.
Les babyloniens semblent avoir utilisé une méthode d'extraction correspondant à deux itérations de Newton.
Travaux pratiques
Calculer l'inverse et la racine carrée d'un nombre donné, en utilisant la méthode de Newton.
Extraction d'une racine carrée
Présentation de la méthode
Cette méthode d'extraction de racines carrées nécessite $\frac{n}{2}$ multiplications d'un entier long par un court (pour une racine d'un nombre de n chiffres) :
- On décompose le nombre en tranches de deux chiffres en partant de la droite : 89 41 52 13.
- On part de la tranche de gauche : on cherche le plus grand entier x dont le carré est inférieur à ce nombre (ici, x=9).
- On soustrait ce carré à la première tranche :

- On cherche le plus grand y tel que [2x]y.y, obtenu en :
- doublant x (9*2=18),
- concaténant les chiffres obtenus à ceux de y,
- multipliant le nombre résultant par y,
| 181*1 < 841 | 184*4 < 841 |
| 182*2 < 841 | 185*5 > 841 |
| 183*3 < 841 |
- On soustrait, on abaisse une tranche, etc.
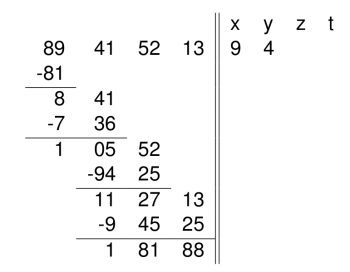
Et alors $9455^2+18188 = 89415213.$
Travaux pratiques
Calculer l'inverse et la racine carrée d'un nombre donné, en utilisant la méthode de Newton.
Le delta-2 d'Alexander Aitken (1926)
Présentation de la méthode
Soit une suite $(x_n)_{n \in \mathbb{N}}$ qui "ressemble" à une suite géométrique, et qui converge vers une limite $l$.
Alors la nouvelle suite $t_n = \frac{x_n x_{n-2} - x_{n-1}^2}{x_n-2 x_{n-1} + x_{n-2}}$ converge plus rapidement vers $l$.
Domaine d'application
Ce principe marche pour toutes les suites qui vérifient $\frac{x_{n+2}-x_{n+1}}{x_{n+1}-x_n} \longrightarrow b, b \in [-1;0[ \cup ]0,1[$
C'est, en ce sens, que l'on parle de ressemblance à une suite géométrique. On parle encore, dans ce cas, de convergence linéaire.
Améliorations possibles ?
Cas des suites à convergence linéaire
On a prouvé qu'il n'existait pas de formule algébrique plus simple qui accélère toutes les suites à convergence linéaire.
De plus, le taux d'accélération de convergence (la puissance 1 du dénominateur) ne peut pas être amélioré en $1+\epsilon$ : il n'existe pas de méthode transformant $x_n$ en $t_n$, et de $\epsilon >0$, tels que : $\frac{|t_n-l|}{|x_n-l|^{1+\epsilon}}\longrightarrow O$
Cas des autres suites
Dans le cas des suites logarithmiquement convergentes $\frac{l-x_{n+1}}{l-x_n} \longrightarrow 1$, comme dans le cas des suites rapidement convergentes :
- on sait en accélérer certaines,
- mais on a prouvé qu'aucune méthode ne pourrait accélérer toutes ces suites.
Travaux pratiques
- Programmer cette méthode.
- Illustrer l'accélération de convergence sur certaines suites bien choisies.
- Mesurer l'accélération de convergence.
La méthode de Karatsuba
Présentation de la méthode
La multiplication habituelle nécessite $O (\frac{n}{2})$ opérations élémentaires.
Une simple réorganisation des calculs a conduit à un réel gain en complexité.
Méthode de Karatsuba
A. Karatsuba le premier, en 1962, observa qu'un entier de taille 2k peut s'écrire $a+b.10^k$ où a et b ont k chiffres, et alors un produit s'écrit :
$(a+b.10^k)(c+d.10^k) = ac-[(a-b)(c-d))-ac-bd].10^k + bd.10^k$
Bref, multiplier deux entiers de taille 2k revient à multiplier trois entiers de taille k, soit $O \left(n^{log_2 3} \right) = O (n^{1,58})$ opérations élémentaires.
Généralisation
En généralisant le procédé, on montre que $\forall \epsilon >0$, on peut définir une manière de multiplier dont la complexité est en $O \left(n^{1+\epsilon} \right)$.
On pense cependant qu'il est impossible de multiplier en $O(n)$.
Travaux pratiques
Programmez cette méthode.