WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Les Automates Finis
Automates finis
Introduction
On va dégager dans ce paragraphe la notion de machine comme modèle conceptuel pour la description de dispositifs informatiques aussi variés qu'un ordinateur entier, un logiciel ou un compilateur.
Définition (Machine)
Une machine est un dispositif doté d'un certain nombre d'états, susceptible d'évoluer d'un état à un autre en fonction de divers paramètres, comme le temps (la machine est alors dotée d'une machine interne).
Elle est de plus apte à communiquer avec l'extérieur : elle peut accepter des données en provenance de l'extérieur (des entrées) ou communiquer des résultats à l'extérieur (des sorties).
Exercice : Donnez des exemples de machines.
Remarque : À chaque instant, la condition interne de la machine, y compris la mémoire, constitue son état.
Mécanismes
Définition
C'est le type le plus simple de machine :
Définition (Mécanisme)
Un mécanisme est totalement imperméable au monde extérieur, il n'accepte aucune entrée ni aucune sortie.
C'est une machine à nombre fini d'états, dont le comportement est gouverné uniquement par le temps, mesuré par une horloge interne.
Exercice : Donner un exemple de mécanisme.
Un mécanisme peut être entièrement décrit par un couple $(E,t)$, où $E$ est un ensemble fini d'états et $t : E \rightarrow E$ est une fonction de transition des états.
Évolution
Théorème (Existence d'un cycle)
Un mécanisme entre nécessairement dans une boucle infinie (on dit : un cycle ).
En effet, le nombre d'états est fini.
Définition (État-repos)
S'il existe un état $e \in E$ tel que $t(e)=e$, cet état est appelé état-repos .
Remarque : Un mécanisme qui entre dans un tel état n'en sort évidemment plus.
Exemple
Exemple : Un feu de circulation routière peut être décrit par un mécanisme à trois états : $V$, $O$ et $R$, donc $E=\{V,O,R\}$.
La fonction de transition des états est telle que $t(V)=O, t(O)=R$ et $t(R)=V$.
On peut représenter ce mécanisme par le graphe de transition des états
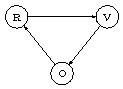
ou par la matrice booléenne $T$ représentant $t$ :
$T = \left( \begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \right)$
Exercice : L'exemple précédent possède-t-il un cycle ? un état-repos ? Sinon, le modifier pour.
Automates finis à comportement déterminé
Présentation
Définition
Définition (Automate fini à comportement déterminé)
On appelle automate fini à comportement déterminé(AFD) tout triplet $(E,I,t)$, où
- $E$ est un ensemble fini (l'ensemble des états),
- $I$ est le vocabulaire de l'automate : c'est l'ensemble fini des symboles admis en entrée,
- $t : E \times I \rightarrow E$ est la fonction de transition d'états : si l'automate se trouve dans l'état $e \in E$, il réagit à l'entrée $i \in I$ en passant à l'état $t(e,i)$.
Pour $i \in I$, on définit la fonction $t_i : E \rightarrow E$ par $t_i(e) = t(i,e)$.
Exemple
Exemple : Soit $E=\{e_0,e_1\}$, $I=\{0,1\}$ et $t$ telle que
- l'entrée 0 laisse inchangé chacun des états,
- l'entrée 1 échange les états.
Un tel dispositif, en électronique, est appelé un T-flip-flop. Il est abondamment utilisé dans les ordinateurs...
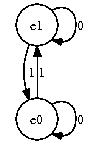
La table qui donne les valeurs de la fonction $t$ est appelée table de transition d'états de l'automate considéré :
| $t $ | $ 0 $ | $ 1 $ |
| $e_0 $ | $ e_0 $ | $ e_1 $ |
| $e_1 $ | $ e_1 $ | $ e_0 $ |
Exercices
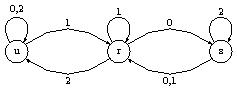
Exercice : Représenter le graphe de l'automate fini $M$ dont la table de transition des états est
| $t $ | $ 0 $ | $ 1 $ | $ 2$ |
| $r $ | $ s $ | $ r $ | $ u $ |
| $s $ | $ r $ | $ r $ | $ s $ |
| $u $ | $ u $ | $ r $ | $ u$ |
Réponse :
Exercice : Écrire la table de transition d'états de l'automate dont le graphe est représenté dans la figure suivante :
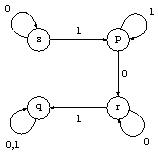
Réponse :
| $ 0 $ | $ 1$ | |
| $p $ | $ r $ | $ p $ |
| $q $ | $ q $ | $ q $ |
| $r $ | $ r $ | $ q $ |
| $s $ | $ s $ | $ p$ |
Automates finis avec sorties (machines de Moore et de Mealy)
Machine de Moore
Définition (Machine de Moore)
Une machine de Moore est un sextuplet $M=(E,I,t,e_0,V,g)$ tel que $(E,I,t)$ est un AFD, et
- $e_0 \in E$ est un état appelé état initial, dans lequel se trouve la machine au départ de chaque exécution.
- $V$ est un ensemble fini, dit ensemble des sorties,
- $g:t<E,I> \rightarrow V$, où $t<E,I>$ est l'image de $t$, est la fonction de sortie telle que, chaque fois que la machine entre dans l'état $e$, elle produise la sortie $g(e) \in V$.
Exemple : Ici, $E=\{e_0, e_1, e_2, e_3\}$, $I=\{0,1\}$, $V=\{a,b,c\}$, $t$ est donnée, soit par le graphe de l'automate :
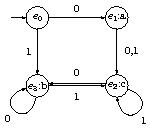
soit par la table de transition d'états
| $t $ | $ 0 $ | $ 1 $ |
| $e_0 $ | $ e_1 $ | $ e_3 $ |
| $e_1 $ | $ e_2 $ | $ e_2 $ |
| $e_2 $ | $ e_3 $ | $ e_2 $ |
| $e_3 $ | $ e_3 $ | $ e_2 $ |
$g$ se lit dans le graphe : $g(e_1) = a, g(e_2) = c, g(e_3) = b$.
Remarque : Une telle machine est aussi appelée traducteur (elle « traduit » l'entrée 0001001 en une sortie $acbcbbc$).
Machine de Mealy
Définition (Machine de Mealy)
On obtient une machine de Mealy lorsque la sortie est déterminée, non pas par l'état atteint, mais par la transition d'états.
C'est donc un sextuplet $(E,I,t,e_0,V,h)$ où la fonction de sortie $h$ est une application de $E \times I$ vers $V$.
Remarque : Il est clair que, pour une machine de Moore $(E,I,t,e_0,V,g)$, on peut définir une machine de Mealy équivalente (c'est-à-dire qui produit la même sortie sur toute séquence d'entrée), en posant $h(e,i) = g(t(e,i))$, soit $h = g o t$.
Réciproquement, en introduisant au besoin des états supplémentaires, on montre qu'on peut remplacer toute machine de Mealy par une machine de Moore équivalente.
Nous ne nous occuperons donc dans la suite que de machines de Moore.
Automates de Moore
Définition (Automate de Moore)
Une machine de Moore telle que l'ensemble $V$ des sorties est réduit à la paire booléenne $\{FAUX, VRAI\}$ ou $\{0,1\}$,
- tout état qui donne lieu à FAUX est appelé état de rejet,
- tout état qui donne lieu à la sortie VRAI est appelé état d'acceptation .
est appelée automate de Moore ou machine d'acceptation.
Remarque : Inutile d'exhiber ici la fonction de sortie, il suffit de se donner l'ensemble $A$ des états d'acceptation, sous-ensemble de $E$.
Un automate de Moore est donc défini par le quintuplet $(E,I,t,e_0,A)$.
Sur le graphe représentant un automate de Moore, on représentera un état d'acceptation en l'entourant d'un double cercle.
Les autres états (simplement cerclés) sont les états de rejet.
Langage associé à un automates de Moore
Définition du langage
Soit $M$ un automate de Moore.
L'ensemble des entrées $I$ peut être considéré comme l'alphabet d'un système formel.
L'ensemble des « mots » construits avec cet alphabet (suite d'éléments de l'alphabet) qui conduisent la machine à un état d'acceptation peut être considéré comme l'ensemble des formules bien formées de ce système formel.
Définition (Langage)
Ce système formel constitue le langage associé à l'automate $M$.
Notation: $\mathcal{L}(M)$
Réciproquement, étant donné un langage $\mathcal L$, on peut éventuellement construire un automate de Moore $M$ tel que le langage associé à $M$ soit $\mathcal L $ : $\mathcal{L} = \mathcal{L} (M)$.
Remarque : Cela n'est pas possible pour tous les langages. Quand c'est possible, cet automate analyse les mots du langage.
Exemple et exercices
Exemple : Construction de l'automate qui reconnaît le langage défini par l'expression suivante...
Un mot du langage est constitué d'un nombre quelconque, mais non nul, de 0, suivi d'un nombre quelconque, mais non nul, de 1.
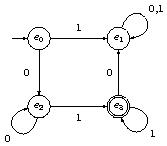
Exercice : Décrire le langage $\mathcal{L}(M)$ de l'automate de Moore $M$ dont la table de transition des états est :
| $t $ | $ 0 $ | $ 1 $ |
| $e_0 $ | $ e_1 $ | $ e_2 $ |
| $e_1 $ | $ e_1 $ | $ e_2 $ |
| $e_2 $ | $ e_2 $ | $ e_1 $ |
L'état initial est $e_0$ et le seul état d'acceptation est $e_2$.
Réponse : Les mots corrects contiennent un nombre impair de 1.
Exercice : Sur l'alphabet $I = \{0,1\}$, construire l'automate de Moore dont le langage est l'ensemble de tous les mots sur $I$ se terminant par 10.
Réponse :
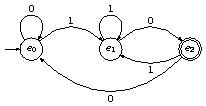
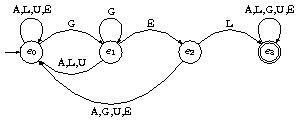
Exercice : Construire un automate de Moore dont l'alphabet est constitué des lettres du mot « ALGUE» qui reconnaît les mots contenant la sous-chaîne « GEL» (et seulement celle-ci).
Réponse :
Automates finis à comportement non déterminé
Définitions et exemples
Automate fini non déterministe
Les automates considérés jusqu'à présent ont un comportement complètement « déterminé » : pour chaque configuration état-entrée $(e,i) \in E \times I$, une et une seule transition d'état est fixée.
Cela résulte du fait qu'ils sont régis par une fonction de transition d'états $t$ (de $E \times I$ dans $E$).
On peut imaginer des automates moins « rigides », pour lesquels, dans certaines configurations, plusieurs transitions d'états sont possibles ou, au contraire, aucune n'est prévue.
Pour un tel automate, qualifié de non-déterministe, $t$ n'est plus une fonction, mais une relation binaire quelconque. Ainsi...
Définition (Automate fini non déterministe)
Un automate fini non déterministe à états d'acceptation est défini par $(E,I,t,S,A)$ où :
- $E$ est un ensemble (fini) d'états,
- $I$ est l'ensemble des entrées,
- $t$ est la relation de transition des états,
- $S$, partie de $E$, est l'ensemble des états initiaux,
- $A$, partie de $E$, est l'ensemble des états d'acceptation.
Remarque : Il se peut donc qu'une entrée puisse conduire un automate vers plusieurs états possibles ou qu'elle laisse l'automate indifférent.
Exemple
Exemple :
Dans cet exemple, lorsque l'automate se trouve dans l'état $e_0$, l'entrée $a$ peut le faire passer dans l'état $e_1$ ou dans l'état $e_3$ et, lorsqu'il se trouve dans l'état $e_1$, rien n'est prévu pour l'entrée $b$.
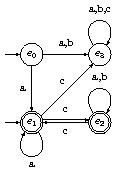
Table de transitions
| $t $ | $ a $ | $ b $ | $ c $ |
| $\{e_0\} $ | $ \{e_1, e_3\} $ | $ \{e_3\} $ | $ ∅ $ |
| $\{e_1\} $ | $ \{e_1\} $ | $ ∅ $ | $ \{e_2, e_3\} $ |
| $\{e_2\} $ | $ \{e_2\} $ | $ \{e_2\} $ | $ \{e_1\} $ |
| $\{e_3\} $ | $ \{e_3\} $ | $ \{e_3\} $ | $ \{e_3\} $ |
Entrée reconnue
Définition
Il est évidemment possible de concevoir des AFND produisant des sorties, et, en particulier, des états d'acceptation et de rejet. On admettra par ailleurs qu'il puisse y avoir, dans ces cas, plusieurs états initiaux possibles.
Soit alors $M=(E,I,t,S,A)$ un AFND.
Définition (entrée reconnue)
On dit qu'une suite $w$ d'entrées est reconnue par l'automate si cette suite peut conduire l'automate à un état d'acceptation.
Exemple : Dans l'exemple précédent,
- Comme $e_1$ est à la fois un état initial et d'acceptation, le mot vide fait partie du langage reconnu par l'automate.
- Le mot $aaacc$ est reconnu par l'automate.
- Les mots refusés sont ceux qui n'ont aucun chemin vers un état d'acceptation, comme $bbb$.
On définit aussi de cette manière le langage $\mathcal{L}(M)$ associé à un AFND. Il est constitué de l'ensemble des mots qui, depuis l'un des états initiaux, peut conduire à l'un des états d'acceptation.
Exercice
Exercice : On considère l'automate fini $M$ non déterministe dont la relation de transition des états est donnée par la table
| $t $ | $ 0 $ | $ 1 $ |
| $e_0 $ | $ e_0, e_1 $ | $ e_1 $ |
| $e_1 $ | $ - $ | $ e_2 $ |
| $e_2 $ | $ e_2 $ | $ e_1 $ |
| $e_3 $ | $ - $ | $ e_0, e_1, e_2 $ |
Si $e_0$ et $e_1$ sont les états initiaux et si $e_2$ est le seul état d'acceptation, les mots 001111 et 01001 sont-ils reconnus par $M$ ?
Réponse : 001111 est reconnu, mais pas 01001.
Utilité
Les AFND sont beaucoup plus simple à construire que les AFD.
Ainsi, les algorithmes de construction automatique d'automates produisent des AFND, et les algorithmes de simplification d'automate utilisent des AFND.
Mais, étant non déterministes, ils ne sont pas programmables. Heureusement, on sait les déterminiser (i.e. construire un automate de Moore qui reconnaît le même langage)...
Exercices
Automates et longueur
Exercice : Soit $\Sigma = \{a, b\}$.
- Fabriquer un automate qui accepte les mots de longueur pair.
- Fabriquer un automate qui accepte les mots de longueur impair.
- Fabriquer un automate qui accepte les mots dont la longueur est congrue à 1 modulo 4.
Propriétés d'un automate à $n$ états
Exercice : Soit un automate fini déterministe $A$ qui a $n$ états et qui n'a pas d'état inaccessible.
Montrer qu'il existe nécessairement un mot de longueur inférieure où égale à $n-1$ qui est accepté par $A$.
Les palindromes
Exercice : [Palindrome] Soit $\Sigma$ un alphabet dont le nombre de caractères est supérieur ou égal à deux.
On appelle retournement l'application $\rho: \Sigma^* \rightarrow \Sigma^*$ telle que $\rho(\epsilon) = \epsilon$ et qui associe au mot $\sigma$ de longueur non nulle le mot $\tau$, nommé retourné de $\sigma$ défini par $\tau(k) = \sigma(n-k+1)$
- Déterminer $\rho(\sigma)$ quand $\sigma = aabcdea$. D'une façon générale, comment le retournement opère-t-il sur la chaîne de caractères qui représente un mot?
- Exprimer $\rho(\sigma\tau)$ en fonction de $\rho(\sigma)$ et $\rho(\tau)$. Que vaut $\rho(\rho(\sigma))$?
- On dit qu'un mot $\sigma$ est un palindrome si $\rho(\sigma) = \sigma$. Montrer que tout mot de la forme $\rho(\sigma)\sigma$ est un palindrome. Est-ce là tous les palindromes?
- Si le nombre d'éléments de $\Sigma$ est $n$, combien y a-t-il de palindromes de longueur $p$ dans $\Sigma^*$?
Exercice : [Suite palindrome] Soit $\Sigma=\{a,b\}$. Construire un AFD qui accepte les palindromes de longueur 3.
Exercice : Soit $\Sigma=\{a,b\}$. On note $L$ le langage constitué des mots dans lesquels la lettre $a$, quand elle apparaît, est toujours suivie d'au moins deux lettres $b$.
- Quels sont les mots de $L$ de longueur inférieure ou égale 6?
- Construire un AFD qui accepte $L$.
- Donner une expression régulière qui décrit $L$.