WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Infographie
Largement inspiré de wikipedia... Sont à traiter
Les différentes manières de mémoriser une scène
Géométrie constructive de solides
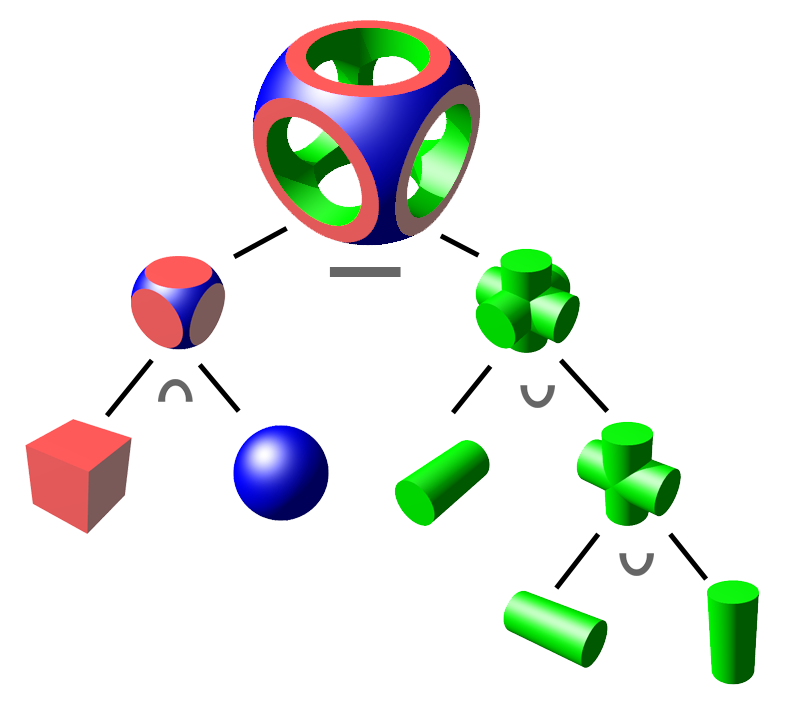
Un objet solide complexe est représenté comme une combinaison d'objets solides simples (ex: cylindre, sphère, cône, tore, etc.) à l'aide d'opérateurs géométriques booléens (union, intersection, soustraction).
Les objets solides simples
Les opérateurs géométriques
- [Union] Le résultat est la juxtaposition des deux objets.
- [Intersection] Le résultat est la partie commune aux deux objets.
- [Différence] Le résultat est le premier objet moins l'intersection
Par exemple, pour un cube plein et une boule :
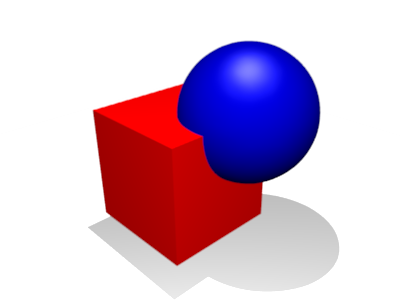
Union

Intersection

Différence
Avantages et inconvénients
- + : les volumes complexes supportent parfaitement l'agrandissement ;
- + : modélisation adaptée au lancer de rayon (cf ci-dessous) : cet algo effectue principalement des intersections de demi-droites avec des volumes mathématiques ;
- + : les calculs de collision entre deux solides convexes sont très rapides : il suffit de tester si au moins un des deux a un point inclus dans l'autre;
- - : solides pas très réalistes : même un ballon posé sur le sol n'est pas parfaitement sphérique.
Représentation par frontière
Un tel modèle est composé de :
- les faces: chacune est une partie bornée d'une surface (planaire dans le cas basique)
- les arêtes : chacune est une partie bornée d'une courbe (droite dans le cas basique)
- les noeuds : les extrémités des arêtes ;
- la coquille : un ensemble de faces connectées.
Modifier des éléments de la scène
Les coordonnées 3D pourront être représentées à l'aide d'un vecteur à trois coordonnées $(x,y,z)$ ou un vecteur à quatre coordonnées $(x,y,z,1)$ comme dans le système de coordonnées homogènes. Les opérations ci-dessous seront différentes suivant les deux cas.
Translations
Coordonnées classiques
Le point $N(N_x,N_y,N_z)$ qui est l'image de $M(x,y,z)$ par la translation selon le vecteur $\vec{T} = (T_x,T_y,T_z)$ est
$ \left[ \begin{array}{l} N_x \\ N_y \\ N_z \end{array} \right]$ = $ \left[ \begin{array}{l} T_x + x \\ T_y + y \\ T_z + z \end{array} \right]$
Coordonnées homogèmes
Le point $N(N_x,N_y,N_z,1)$ qui est l'image de $M(x,y,z,1)$ par la translation selon le vecteur $\vec{T} = (T_x,T_y,T_z,1)$ est
$ \left[ \begin{array}{l} N_x \\ N_y \\ N_z \\ 1 \end{array} \right]$ = $ \left[ \begin{array}{4} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{l} x \\ y \\ z \\1 \end{array} \right]$
Rotations
Coordonnées homogènes
$ R_{\alpha,x} = \left[ \begin{array}{4}1 & 0 & 0 & 0 \\ 0 & \cos( \alpha ) & \sin \alpha) & 0 \\ 0 & \sin( \alpha ) & \cos ( \alpha) & 0 \\ 0 & 0 & 0 & 1 \end{array} \right]$,
$R_{\alpha,y} = \left[ \begin{array}{4}\cos(\alpha) & 0 & \sin(\alpha) & 0 \\ 0 & 1 & 0 & 0 \\ -\sin( \alpha ) & 0 &\cos ( \alpha) & 0 \\ 0 & 0 & 0 & 1 \end{array} \right]$
et
$R_{\alpha,z} = \left[ \begin{array}{4} \cos(\alpha) & - \sin(\alpha) & 0 & 0 \\ \sin(\alpha) & \cos(\alpha) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right]$.
pour $u$ valant $x$, $y$ ou $z$, le point $N(N_x,N_y,N_z,1)$ qui est l'image de $M(x,y,z,1)$ par la rotation d'angle $\alpha$ autour de l'axe $u$ est obtenu grâce au produit matriciel suivant :
$ \left[ \begin{array}{1} N_x \\ N_y \\ N_z\\ N_w \end{array} \right] = R_{\alpha,u} \cdot\left[\begin{array}{1}x \\ y \\ z \\ 1 \end{array} \right]$.
Algorithmes d'affichage d'une scène 3D
Sélection des faces mal orientées (F. Roberts)
Permet de sélectionner les faces visibles d'un volume convexe. Par convention, les points des faces visibles sont classés dans le sens contraire des aiguilles d'une montre. Si la normale de la face est dans la direction de l'axe optique, alors la face est invisible. Sinon elle est visible.

Dans l'exemple précédent (extrait de http://perception.inrialpes.fr/people/Boyer/Teaching/RICM/c6.pdf),
- en $P1$, la normale au plan est dans la direction contraire de l'axe optique, il est visible
- en $P2$ et en $P3$ la normale est perpendiculaire à l'axe optique. Le plans sont à la limite de visibilité
- en $P4$ la normale est dans le sens de l'axe optique. Ce plan est invisible.
Cet algorithme a de nombreuses limitations. Lesquelles?
L'algorithme du peintre
Principes
L'« algorithme du peintre » fait référence à un peintre qui dessinerait les parties lointaines d'une scène avant les parties proches.
L'algorithme du peintre trie les polygones de la scène par rapport à leur distance de la camera, du plus éloigné au plus proche, et les dessine dans le même ordre : du plus éloigné au plus proche
Les polygones les plus lointains sont dessinés avant les plus proches: ces derniers sont peints par dessus premiers et les recouvrent donc.
L'algorithme s'exécute selon trois étapes principales:
- Trier les polygones suivant leur distance à la caméra
- Résoudre les ambiguïtés dans la liste lorsque les polygones se recouvrent (voir ci dessous)
- Projeter les facettes sur le plan écran et remplir les polygones suivant la liste.
Résolution des ambiguïtés
On peut avoir les cas suivants :
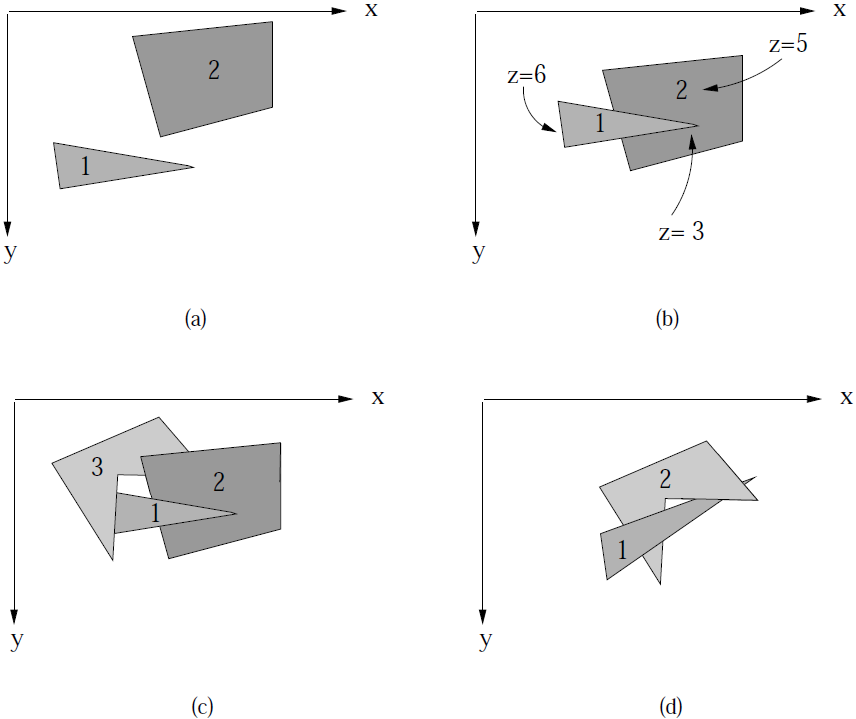
- (a): calculer les projections dans le plan d'affichae et constater que l'intersection est vide.
- (b): remarquer que tous les points du polygone 2 sont du du même côté du plan du polygone 1.
- (c) et (d): difficile !