WikiMath

Ce TP s'inspire largement du TP de Rémi Megret

Présentation générale

L'objectif de ce TP est de programmer la méthode d'identification de visages dite par "eigenfaces", proposée par Turk et Pentland en 1991. Cette méthode permet de reconnaître à la volée une personne sans s'intéresser à des caractéristiques particulières comme la couleur des yeux, la forme du visage, celle du nez... L'idée principale est de décrire chaque visage comme une combinaison de vecteurs. Ces vecteurs de base sont les eigenfaces. Ils sont calculés automatiquement comme étant ceux qui discriminent le mieux les visages dont on connait déjà les identifiants.

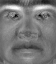
Dans l'exemple ci-dessous, l'image la plus à gauche (yaleB13) est la somme

• de la seconde image (moyenne de toutes les images) avec
• -14.4 la troisième image (eigenface1)
• 5.4 la quatrième image (eigenface2)
• 0.3 la cinquième image (eigenface3)
• 3.4 la sixième image (eigenface4)
• -0.1 la septième image (eigenface5)

Objectifs du TP

Ce qui suit est une méthode pas à pas permettant de développer un système capable de reconnaître avec une certaine fiabilité un visage d'une base de données de visages de références. Ceci se fait en XXX étapes :

1. Construire un sous-espace d'eigenfaces
2. Projection dans un sous-espace d'eigenfaces
3. Identification de l'image grâce aux projetés

Outils à télécharger

Le TP s'appuie sur un extrait de la base de visages de Yale. La première étape consiste à récupérer ce fichier, le décompresser et le parcourir.

De l'image au vecteurs de flottants

Le dossier contient $m=38$ visages éclairés différemment, pris sous des angles légèrement différents. Les visages de base sont ceux dont le suffixe est "_P00A+000E+00.pgm". On note que tous les images ont une taille de 64 lignes et 56 colonnes soit $n=3584$ pixels.

Dans la suite par soucis de cohérence

• une image est toujours mémorisée comme un vecteur à une colonne et 3584 lignes.
• le vecteur $I_{\textit{moy}}$ est la moyenne de $I_1$,$\ldots$, $I_m$. Il représente le visage moyen parmi les visage déjà identifiés.
• un ensemble de $m$ images est toujours mémorisé comme une matrice

de $m$ colonnes où chaque colonne est un vecteur représentant une image. Ainsi l'ensemble des visages de base est la matrice $I=\left[ I_1,\ldots,I_m\right]$ de taille $n\times m$

Construire un sous-espace d'eigenfaces

Travaux pratiques préliminaires

1. Construire la matrice $I$ de tous les visages dont le dont le suffixe est "_P00A+000E+00.pgm".
2. Construire le vecteur $I_{\textit{moy}}$ et l'afficher.

Construire le vecteur d'eigenfaces

A l'origine, les eigenfaces sont les axes principaux obtenus en effectuant l'Analyse en Composantes Principales des vecteurs associés aux visages de référence.

Théoriquement, les eigenfaces sont les vecteurs propres de la matrice de $A.A^{T}$, de taille $n\times n$, où la matrice $A$ de même taille que $I$ représente l'ensemble des visages centrés : $A = \left[ I_1-I_{\textit{moy}}, \ldots, Im-I_{\textit{moy}} \right]$ Intuitivement, les eigenfaces sont les vecteurs qui permettent de séparer au mieux les colonnes de $A$ par projection.

1. Construire la matrice $A$.
2. La fonction numpy.linalg.svd(A, full_matrices=0) retourne

$(u,s,v)$ où

• les $s$ sont les valeurs propres classées par ordre décroissant
• les $u$ sont les vecteurs propres associées à ces valeurs propres
• $v$ est une matrice dont on ne se sert pas.

Exploiter cette fonction pour retourner les 5 première eigenfaces.

1. Afficher les cinq premières eigenfaces

Projection dans un sous-espace d'eigenfaces

Formalisation

On construit la base $W_K = \left[ U_1,\ldots,U_K \right]$ des $K$, $1\le K \lem$, premières eigenfaces. Ceci permet de construire un sous espace des visages.

La projection d'une image $I$ de test dans le sous-espace des eigenfaces se fait en soustrayant le visage moyen et en effectuant le produit scalaire de l'image obtenue avec chaque eigenface. Ceci donne les coordonnées de l'image test dans le sous-espace des visages, qui est de dimension $K$. Ainsi pour chaque $k$, $ 1 \le k \le K $, on a $ c_I(k) = U_k^T . (I – I_{\textit{moy}})$

Chaque visage possède donc deux représentations :

• son image d'origine, représenté par un vecteur $I $ dans $\{0,1,\ldots,255 \}^{n}$;
• ses coordonnées $\left[ c_I(1),\ldots, c_I(K) \right]$ dans la base des eigenfaces;
• son image projetée dans le sous-espace des visages, $I^{\textit{proj}}$ définie par $I^{\textit{proj}} = I_{\textit{moy}} + \sum_{k= 1}^K c_I(k) U_k$

Ainsi, avec $m$ visages, nommés $I_1, \ldots, I_m$, avec la matrice $A=\left[I_1-I_{\textit{moy}},\ldots, I_m-I_{\textit{moy}}\right]$ qui représente les $m$ visages centrés, on obtient les coordonnées $C_{I1},\ldots, C_{Im}$ directement en effectuant le produit $\left[C_{I1}, \ldots, C_{Im}\right] = W^T.A$

Travaux pratiques

1. On considère $K=5$. On a donc 5 eigenfaces. Chaque image va donc être être réduite à 5 coordonnées. Calculer la matrice des coefficients $C_I$ $ [C_{I1},\ldots,C_m] $

Identification

Formalisation

A chaque visage de référence $I_k$ est associée une identité, sous la forme d'un numéro $\textit{id}(k)$.

Nous chercherons maintenant à identifier un visage test $J$ à partir des visages de référence, c'est à dire à trouver quel est l'identité $\textit{id}(k)$ de $J$. Pour cela, on calcule pour chaque image de référence $I_k$ la distance $d(J,I_k) = ||J^{\textit{proj}} - I_k^{\textit{proj}}||$ entre les projections $J^{\textit{proj}}$ et $I_k^{\textit{proj}}$. On trouve ensuite le $k$ qui minimise cette distance.

Si ce minimum est inférieure à un seuil $s$ , on peut estimer qu'il s'agit d'un visage reconnu d'identité $\textit{id}(k)$, sinon le visage est classifié comme inconnu.

Travaux pratiques

Dans ce qui suit, on considère que $K=5$.

1. Mémoriser pour chaque $k$ entre 0 et 37 son identité, c.-à-d. le nom du fichier associé
2. Implanter la fonction d(J) qui prend en paramètre un visage $J$
   1. qui calcule le $d(J,I_k)$ donné ci dessous pour tous les $k$ entre 0 et 37
   2. qui en déduis le minimum
   3. retourne le minimum ainsi que l'indice $k$ ayant généré ce minimum.