WikiMath

L'algorithme exposé dans ce paragraphe est appelé méthode de construction par sous-ensemble. Il s'agit d'une méthode qui permet d'obtenir un automate de Moore qui reconnaît le même langage qu'un AFND.

Méthode de construction par sous-ensemble

Soit donc $M=(E,I,t,S,A)$ un AFND à états d'acceptation. Soit $Y$ une partie quelconque de $E$ et $x \in I$ une entrée quelconque.

Notation: On note $Y_x$ l'ensemble des états de $M$ accessibles à partir de l'un quelconque des états de $Y$ sur l'entrée $x$.

Exemple : Dans l'exemple suivant,

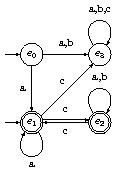
et pour $Y = \{ e_1, e_3\}$ :

• $Y_a = \{e_1\} \cup \{ e_3 \} = \{e_1, e_3 \}$,
• $Y_b = \{e_3\} \cup ∅ = \{ e_3 \}$,
• $Y_c = \{e_2, e_3\} \cup \{ e_3 \} = \{e_2, e_3 \}$,

On obtient un automate de Moore $\mathcal{M} = ( \mathcal{E}, \mathcal{I}, T, E_0, A)$ de la manière suivante :

• L'ensemble $\mathcal{E}$ des états de $\mathcal{M}$ est le sous-ensemble de $P(E)$ défini par :
  • $S \in \mathcal{E}$,
  • $\forall x \in \mathcal{I}, \forall Y \in \mathcal{E}, Y_x \in \mathcal{E}$.
• L'état initial de $\mathcal{M}$ est $E_0=S$.
• L'ensemble $A$ des états d'acceptation de $\mathcal{M}$ est défini par $A=\{Y \in \mathcal{E} \| Y \cap A \neq \emptyset \}$.
• La fonction de transition d'états est définie par $T : \mathcal{E} \times \mathcal{I} \rightarrow \mathcal{E}, (Y,x) \longmapsto T (Y,x) = Y_x$.

Comment procéder en pratique

En pratique, on part de l'état initial de $\mathcal{M}$, c'est-à-dire de $S$.

Pour chacune des entrées, on forme l'ensemble $S_x$ des états de $M$ que la relation de transition $t$ permet d'atteindre à partir de tous les états de $S$, et on pose $T (S,x) = S_x$.

On recommence l'opération pour chacun des états $S_x$ ainsi obtenus (pour les diverses entrées $x$), etc.

Remarque : Le processus a une fin, parce que $E$ est fini, donc aussi $P(E)$ : si l'automate de départ a $n$ états, l'automate déterminisé en aura au plus $2^n$..

Remarque : Il se peut qu'aucun état ne soit accessible depuis l'un quelconque des états d'un état $Y_x$ de $\mathcal{M}$, sur une entrée $y$.

On prend alors pour état d'arrivée de $\mathcal{M}$ l'ensemble vide ; celui-ci constitue un état particulier de $\mathcal{M}$, dont on ne peut sortir sur aucune entrée (c.f. exemple ci-dessous).

Exemple : Un exemple...

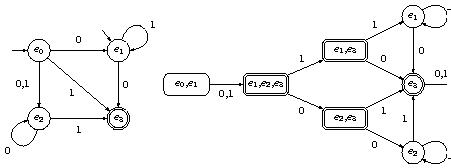
Travaux pratiques

Programmation

1. Utiliser le module FSA pour faire un programme recevant un AFND, et renvoyant son déterminisé.
2. Vérifier, avec ce programme, que l'exemple de déterminisation ci-dessus est correct.

Exercice

Résoudre l'exercice suivant, à la main et avec votre programme.

Exercice : Construire des automates de Moore équivalents aux AFND ci-dessous :

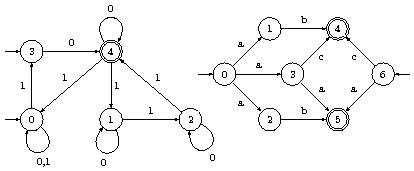
Utilisation de FSA

Le module FSA permet de déterminiser un automate, comme suit :

  >>> automate.determinized()

Vérifiez vos résultats avec cette méthode.