WikiMath

L'algorithme exposé ici est appelé algorithme de Thompson. Il permet de construire un AFND à partir d'une expression rationnelle.

Automates à transitions instantanées

Définition (Transition instantanée)

Une transition instantanée est une évolution possible de l'automate d'un état vers un autre sans qu'aucune entrée ne soit produite.

Les automates à transitions instantanées interviennent dans l'algorithme de Thompson de construction automatique d'un automate reconnaissant le langage associé à une expression rationnelle...

Données et résultat

Données

une expression rationnelle $r$ sur un alphabet $\Sigma$.

Résultat

Un AFND $M$ tel que $\mathcal{L}(M) = \mathcal{L}(r)$, qui ne comporte qu'un seul état initial et un seul état d'acceptation...

Algorithme

Décomposer l'expression en ses sous-expressions.

En utilisant les règles ci-dessous, construire un AFND pour les symboles terminaux de la grammaire ou la chaîne vide. (Si un même symbole $a$ apparaît plusieurs fois dans l'expression rationnelle, un AFND séparé est construit pour chacune de ses occurrences.)

Combiner ensuite récursivement les AFND de base jusqu'à obtenir l'AFND pour l'expression rationnelle toute entière.

• Pour $< >$, construire l'AFND :

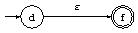
• Pour $a \in \Sigma$, construire l'AFND :

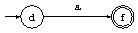
• Si $N(s)$ et $N(t)$ sont les AFND pour les expressions rationnelles $s$ et $t$,
  • Pour $st$, on construit l'AFND :

L'état initial de $N(t)$, qui est état d'acceptation pour $N(s)$, perd ce double caractère dans la nouvelle construction.

• Pour $s|t$, on construit l'AFND

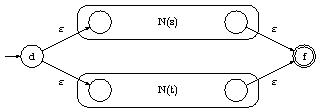
Les états initiaux et les états d'acceptation des AFND de $N(s)$ et de $N(t)$ perdent leur caractère dans le nouvel AFND.

• Pour l'expression rationnelle $s^*$, on construit l'AFND composé $N(s^*)$ :

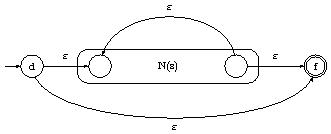
• Pour une expression parenthésée $(s)$, utiliser $N(s)$ lui-même.

Exemple

On applique l'algorithme sur l'exemple : $(a^2|b^2)^*|(a^3|b^3)^*$.

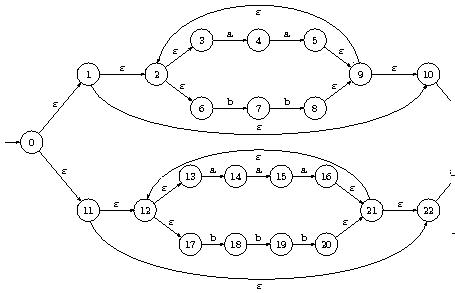
Exercice : On donne l'expression rationnelle $(a | b)^* | (a^2 | b^2)^*$.

Utiliser l'algorithme de Thompson pour obtenir un automate non déterministe, à transitions instantanées, reconnaissant le langage.

On rappelle que, par définition, sont accessibles sur une entrée donnée $x$ depuis un état donné $e$ : les états accessibles en effectuant successivement

• un nombre arbitraire (éventuellement nul) de transitions instantannées,
• une transition d'entrée $x$ et
• un nombre arbitraire (éventuellement nul) de transitions instantannées.

Exemple : Pour...

• L'état 3, avec entrée $a$ : on passe à l'état 4.
• Si l'entrée $a$ se produit au départ, les états accessibles sont $\{ 4, 14 \}$.
• Et, à partir de l'état 4 et de l'entrée $a$ : $\{ 5, 9, 2, 10, 23, 3, 6 \}$.

La variable « état initial » d'un automate de Thompson est constituée de l'état initial et de tous les états accessibles depuis celui-ci par un nombre quelconque de transitions instantannée :

$\{ 0, 1, 11, 2, 10, 12, 22, 3, 6, 13, 17, 23 \}$

D'où l'algorithme suivant simplifiant l'automate de l'algorithme de Thompson...

Finalisation

L'automate construit par algorithme de Thompson n'est pas utilisable tel quel.

Il faut en supprimer les transitions instantanées, ce qui se fait par un algorithme voisin de la construction par sous-ensembles. Il faudra, par ailleurs, ensuite, le déterminiser et le minimiser.

Soit $M$ l'automate de Thompson obtenu par l'algorithme précédent, $E$ l'ensemble de ses états, $e \in E$ son (unique) état initial et $a \in E$ son (unique) état d'acceptation.

On remplace cet automate par un automate $\mathcal{M}$ qui reconnaît le même langage, dont l'ensemble des états est $\mathcal{E}$, l'état initial est $S$, et l'ensemble des états d'acceptation est $A \subset \mathcal{E}$ et qui est obtenu de la manière suivante :

• $S$ est composé de $e$ et de tous les états de $M$ qui sont accessibles depuis $e$ par un nombre quelconque de transitions instantanées (éventuellement aucune). Dans l'exemple précédent, $S = \{ 0, 1, 11, 2, 10, 12, 22, 3, 6, 13, 17, 23 \}$
• Soit $Y \in \mathcal{E}$ une partie de l'ensemble des états, et $x$ une entrée. L'image $Y_x$ de $Y$ est constituée des états accessibles depuis un état quelconque de $Y$ par (exactement) une entrée $x$, suivie d'un nombre quelconque de transitions instantanées.
• $A = \{ Y \in \mathcal{E} | Y \cap \{a\} \neq \emptyset \}$, à savoir les parties $Y$ ci-dessus définies de $E$ qui contiennent l'ancien état d'acceptation.

Travaux pratiques

Programmation

Réaliser un programme mettant en place l'algorithme décrit ici.

Exercices

Résoudre ces exercices, à la main et avec votre programme.

Exercice : Finalisez l'automate de l'exercice précédent. Le déterminiser, puis obtenir l'automate minimal reconnaissant le même langage.

Exercice : Construire des automates de Moore reconnaissant les langages définis par les expressions rationnelles :

1. $(a|b)^* b (a|b)^*$
2. $((a|b)^2)^* | ((a | b)^3)^*$
3. $ba^*|ab|(a|bb)ab^*$.

Réponses : Pour $(a|b)^* b (a|b)^*$

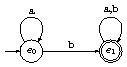
Exercice : Donner les automates finis minimaux (table de transition, diagrame) reconnaissant les langages associés aux expressions rationnelles suivantes :

• $(a|b)^* (aaa|bb)$
• $(a|bb)^* abb^*$

Utilisation de FSA

Le module FSA permet évidemment de faire ce qui précède.

Voici par exemple comment construire et visualiser l'automate reconnaissant $a(b|c^*)$ :

  >>> from FSA import *
  >>> tp= concatenation(singleton('a'),\ 
                        union(singleton('b'),\ 
                        closure(singleton('c'))))
  >>> tp.view()
  >>> td=tp.minimized()
  >>> td.view()

Utilisez le module FSA pour vérifier vos résultats.