---

Le but du présent TP est de se familiariser avec l'utilisation des listes et des matrices en Python. On commencera donc par lire la documentation sur les listes, et les matrices.

Des sujets, autour des carrés magiques et latins, permettent alors de mettre en oeuvre ces connaissances nouvellement acquises.

Les carrés magiques

Présentation

A savoir...

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Définition

Définition : Une matrice (ou un carré), est dit magique si en sommant ses coefficients :

• par ligne,
• par colonne,
• suivant chacune des deux diagonales,

on trouve à chaque fois le même résultat.

En voici une :

$\left( \begin{array}{ccc} 8&1&6\\ 3&5&7\\ 4&9&2 \end{array} \right)$

On remarquera que les matrices magiques forment un sous-espace vectoriel des matrices carrées de taille n.

Utilité

A ceux qui demandent à quoi ça sert, d'aucuns répondraient à la conservation de bâtiments :

• Abraham aurait déposé un carré d'ordre 100 dans les fondations de la Mecque. On utilisa de même des carrés magiques lors de la construction des pyramides d'Egypte.
• Dans certaines traditions islamiques, les carrés magiques empêchent la peste, les épidémies et autres maladies graves de pénétrer dans une maison qui les contient.

Inutile de vous dire ce qu'il faudrait en penser...

Autre réponse, d'Henri Poincaré, peut-être le plus grand mathématicien du XXe siecle : " Le savant n'étudie pas la nature parce qu'elle est utile, Il l'étudie parce qu'il y prend plaisir, et il y prend plaisir parce qu'elle est belle.[...] La beauté intellectuelle se suffit à elle-même."

Algorithme de génération

Pour construire un carré magique M de taille 2*p+1,

• On initialise d’abord ses coeffcients à 0, puis on fait $M_{1,p+1}=1$ (en d'autres termes, on met un 1 au milieu de la première ligne).
• Ensuite, on suit une diagonale sud-ouest/nord-est, pour mettre les entiers 2, 3...

$ \left( \begin{array}{ccc} 0&1&0\\ 0&0&0\\ 0&0&0 \end{array} \right) ~ \left( \begin{array}{ccc} 0&1&0\\ 0&0&0\\ 0&0&2 \end{array} \right) ~ \left( \begin{array}{ccc} 0&1&0\\ 3&0&0\\ 0&0&2 \end{array} \right) $

• Alors, on place l’entier suivant $n$, sous le $n-1$ (ici : le 4 sous le 3), puis on remplis la diagonale :

$\left( \begin{array}{ccc} 0&1&0\\ 3&0&0\\ 4&0&2 \end{array} \right) ~ \left( \begin{array}{ccc} 0&1&0\\ 3&5&0\\ 4&0&2 \end{array} \right) ~ \left( \begin{array}{ccc} 0&1&6\\ 3&5&0\\ 4&0&2 \end{array} \right) $

• On poursuit, jusqu'au remplissage complet du carré.

Travaux pratiques

1. Faire une fonction qui teste si un carré est magique.
2. Mettre en oeuvre l'algorithme de génération d'un carré magique.

Les carrés latins

Origine et définition

L'origine

Leur origine remonte au Moyen Age. Euler les baptisa carrés latins, et les étudia.

La définition

Un carré latin de taille n est une disposition en carré des permutations de n symboles :

1	2	3	4
2	3	4	1
3	4	1	2
4	1	2	3

Dénombrement

Il y a :

• 12 carrés latins de côté 3,
• 576 carrés latins de côté 4,
• environs $5*10^{28}$ carrés latins de côté 9,
• Si on décide que les carrés latins déductibles les uns des autres ne doivent être comptés qu'une fois, il ne reste que $3*10^{18}$ carrés latins de côté 9 (1975).
• Une formule générale, assez compliquée, a été trouvée en 1981 par Nechvatal, pour les compter...mais elle ne permet pas d'en déduire l'ordre de grandeur du nombre de carrés latins de taille n, pour n grand.

Travaux pratiques

1. Faire un programme qui teste si un carré passé en argument d'une fonction est latin ou non.
2. Obtenez tous les carrés latins de taille 3, 4 et 5.
   • On commencera par obtenir tous les carrés de nombres de taille 3, i.e. toutes les matrices $3 \times 3$ constituées uniquement de valeurs prises dans {1, 2, 3}
   • Puis on utilisera la fonction précédente pour écarter les carrés qui ne sont pas latins.
   • On créera une nouvelle fonction qui recevra la taille des carrés à invertiguer, et qui renverra la liste, ou le nombre, de carrés latins de cette taille.
   • On étudiera enfin la possibilité d'utiliser cette dernière fonction pour les carrés de taille $n>5$. Si l'on souhaite aller plus loin, on pourra rechercher des algorithmes plus efficaces sur le net.

Le sudoku

Présentation

Le principe

Tout le monde en connaît le principe...

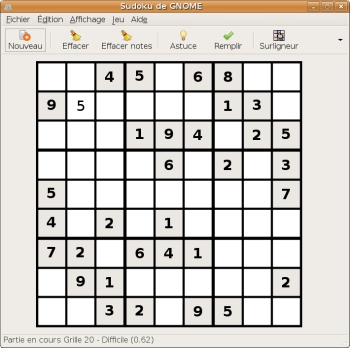
Carré magique ou latin ?

L'ancêtre du sudoku n'est pas, comme on le dit parfois, le carré magique (avec lequel il n'a pas grand chose à voir), mais le carré latin.

En effet, une grille de sudoku est un carré latin d'ordre 9, où les permutations sont telles que chacun des neuf sous-carrés contient les nombres de 1 à 9.

L'origine, l'attrait

Quel origine, et pourquoi un tel attrait ?

• Le sudoku ("nombre seul") est appelé number place au Japon : le charme de l'exotisme...
• Les premiers furent publiés en 1979 dans une revue américaine.
• Son attrait ? chaque nouvelle case remplie rend la solution plus proche, le jeu s'accélère...

Travaux pratiques

1. Faire une fonction qui teste si tout les nombres de 1 à 9 sont présents dans une matrice de taille $3 \times 3$.
2. Faire une fonction qui teste si trois matrices $3 \times 3$ sont compatible, i.e. si elles peuvent être dans la même ligne, ou la même colonne.
3. Faire une fonction qui reçoit une matrice $9 \times 9$, et qui teste si elle est un carré Sudoku.

Dénombrement

Nombre de sudokus

On cherche à connaître le nombre de Sudokus différents...

• Diverses opérations conservent le caractère sudoku d'une grille : rotation, symétrie, permutation des trois premières colonnes, etc.
• Si l'on compte le nombre de sudokus fondamentalement différents, on en trouve un peu plus que d'être humains.
• De plus, une grille de sudoku donne naissance à plusieurs énoncés (personne n'a réussi à compter combien il existe de grilles différentes).

Plus petit nombre de chiffres

Dans le même esprit...

• On ne connaît pas le plus petit nombre de chiffres à placer dans une grille pour que la solution soit unique (16, peut-être).
• Par contre, on ne peut pas avoir plus de 77 chiffres sans avoir l'unicité de la solution.

Résolution

La théorie

Résolution d'un sudoku de taille quelconque

Après le dénombrement, la résolution...

• Le problème de la résolution des grilles de sudoku de taille $n^2 \times n^2$ est NP-complet.
• Cela signifie qu'il sera sans doute impossible d'écrire un programme de résolution efficace des sudokus de taille $n$ quelconque.
• En effet, le temps de résolution augmente si vite en fonction de $n$, que quelque soit le programme, il ne peut plus traiter en temps raisonnable les grilles qu'on lui soumet.

Méthode de résolution d'un sudoku classique (de taille 9)

Plusieurs méthodes sont envisageables pour programmer la résolution du sudoku de base :

• on peut se baser sur une méthode type recuit-simulé.
• Mais la plus courante des résolutions est celle du "retour arrière systématique" : backtracking.

Avec cette dernière, on découvre ainsi toutes les solutions (même s'il y en a plusieurs, si le sudoku est imparfait).

La méthode du backtracking

Présentation de la méthode

La technique du backtracking, appliqué au Sudoku :

1. On place un 1 dans la première case vide,
2. Si ce choix est compatible avec les règles de base, on continue avec la seconde case vide où l'on place un 1, puis avec la troisième, etc.
3. Si l'on rencontre une incompatibilité, on augmente d'une unité le dernier chiffre placé, et on repart en avant,
4. Enfin si, en voulant monter d'une unité le dernier chiffre placé, on trouve un 9, alors on revient à nouveau en arrière, et on augmente d'une unité l'avant-dernier chiffre placé, puis on repart en avant, etc.

Amélioration possible

Une amélioration possible : la propagation des contraintes...

Après chaque chiffre placé nouvellement, le programme met à jour un tableau des possibilités restantes de chaque case vide, et n'envisage de nouveaux chiffres que conformément à ce tableau.

Travaux pratiques

1. Mettre en oeuvre la résolution d'un sudoku par la technique du backtracking.
2. Rajouter l'amélioration de cette méthode signalée ci-dessus.
3. La tester sur l'exemple donné par l'image ci-dessus.

Le recuit simulé

Voir la page concernant le recuit simulé ici.

Génération

Après la résolution, la génération...

Les programmes de génération des grilles fonctionnent ainsi : on place des chiffres au hasard sur une grille, et on applique un algorithme de résolution (type backtracking) :

• si la grille possède une unique solution, c'est ok,
• si la grille ne possède pas de solution, on lui enlève un chiffre, et l'on recommence,
• sinon, on choisit une des solutions, et l'on ajoute (en appliquant l'algorithme) à la grille partielle autant de chiffres nouveaux nécessaires pour que la solution choisie devienne unique.

Travaux pratiques

Si ce thème vous intéresse, vous pouvez...

• Réaliser une interface graphique.
• Généraliser ce qui précède aux sudokus exotiques (autre chose qu'un carré $9 \times 9$).