WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Automates A Pile
On l'a dit, les expressions rationnelles ne permettent pas de représenter tous les langages.
Exemple : Le langage défini par $\{ a^n b^n | n \in \mathbb{N}^* \}$ n'est pas représentable par une expression rationnelle.
Exercice : Déterminez d'autres langages non reconnus par expression rationnelle.
On souhaite maintenant étudier « une plus grande classe» de langages, et voir ce qu'il manque à nos automates pour pouvoir les associer à ces langages.
Dans l'exemple précédent, il faudrait « noter quelque part » le nombre de $a$ rencontrés, pour s'assurer qu'il y aura bien autant de $b$. On peut imaginer y arriver avec une pile jointe à un automate non déterministe.
Remarque : Très précisément, les automates à pile vont jouer pour les langages dits non contextuels (voir chapitre suivant) le rôle des automates finis pour les langages rationnels (: représentables par expressions rationnelles).
Automates à pile, déteministes ou pas.
Automate à pile non déterministe
Définition
Définition (Automate à pile)
Un automate à pile est donné par
- Un alphabet d'entrée $\Sigma$ (ensemble fini non vide),
- Un ensemble d'états $E$ (fini non vide),
- Un état initial $e_0 \in E$,
- Éventuellement, une partie $A \subset E$ des états d'acceptation (pour un automate à pile dit à états d'acceptation),
- Un alphabet de pile $P$ (fini, non vide),
- Un symbole de pile initial $p_0$,
- Éventuellement, un ensemble $Q \subset P$ de symboles de sommet de pile,
- Enfin, une relation $t : E \times (\Sigma \cup \{ \varepsilon \} \} \times P \rightarrow E \times P^*$.
Remarque : Le symbole de pile initial n'est pas toujours noté $p_0$.
Transition
Définition (Transition)
Lorsque $((e,x,p),(e',q))$ appartient au graphe de la relation $t$, on parle de la transition $(e,x,p) \longmapsto (e',q)$.
Elle indique que, lorsque l'automate se trouve :
- dans l'état $e$,
- alors que le symbole de sommet de pile est $p$,
- sur l'entrée $x$,
alors il évolue
- vers l'état $e'$,
- le symbole $p$ est dépilé,
- et le mot de pile $q$ (éventuellement plusieurs symboles de pile) est empilé.
Comme $t$ est une relation, il est possible, dans le cas d'un automate à pile non déterministe, qu'il y ait plusieurs transitions possibles dans la même situation (même état, même entrée, même symbole de sommet de pile).
Exemple : [Automate à pile non déterministe]
Ici, l'alphabet d'entrée est $\{0,1\}$, le fond de pile est $T$ et alphabet de pile $\{T,Z,A\}$ :
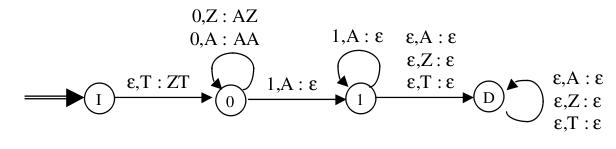
Cet automate reconnaît, par pile vide, l'ensemble $\{0^n 1^m, n \geqslant m > 0 \}$
Remarque : Si un automate à états finis reconnaît un mot lorsqu'il s'arrête dans un état d'acceptation, il n'en est pas de même pour les automates à pile : on verra par la suite que ceux-ci ont plusieurs critères pour décider si un mot est reconnu ou non.
Le critère de reconnaissance par pile vide fait partie de ceux-ci: lorsque l'automate s'arrête avec une pile vide, le mot est accepté.
On remarque que les mots 01, 001, 0011 sont acceptés par cet automate. Il n'en est pas de même pour 011.
Automate à pile déterministe
Définition
Définition (Automate à pile déterministe)
Dans le cas d'un automate à pile déterministe, $t$ est une fonction sur son domaine de définition, et $(e',q) = t(e,x,p)$.
Remarque : En particulier si $t$ est définie pour le triplet $(e,x,p)$, $t(e,x,p)$ est unique.
Exemple : [Automate à pile déterministe] Ici, l'alphabet d'entrée est $\{0,1\}$, le fond de pile est $Z$ et alphabet de pile $\{Z,A\}$ :
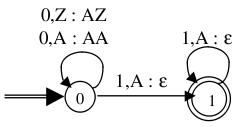
Remarque : Cet automate à pile déterministe reconnaît, par état final, le même langage que l'exemple précédent.
Transitions
Il est fondamental de comprendre qu'une transition d'un automate à pile, quelle qu'elle soit, exige toujours de dépiler un symbole de pile.
Remarque : Autrement dit, si la pile vient à se vider, l'automate se bloque et ne peut plus évoluer, même si le mot d'entrée n'a pas été entièrement lu.
Ceci explique le « symbole de pile initial» , la plupart du temps sans intérêt autre que celui de permettre le début du calcul dans l'automate.
Remarque : On admet des « transitions vides» , du type $(e,\varepsilon,p) \longmapsto )$, qui permettent de ne pas avancer sur le mot d'entrée, par exemple pour vider la pile. Il faut les utiliser avec précautions.
Calcul dans un automate à pile
Encore quelques définitions...
Définition (Configuration)
On appelle configuration d'un automate à pile un triplet $(e,w,q)$ où
- $e$ est l'état dans lequel se trouve l'automate à l'instant considéré,
- $w$ est le mot à lire,
- $q$ est le mot de pile (en tête, le symbole de sommet de pile, en queue, le symbole de fond de pile).
Définition (Dérivation valide)
Si
- $q$ est de la forme $pq'$ où $p$ est le symbole de sommet de pile,
- $w$ est de la forme $xw'$, où $x$ est un symbole d'entrée,
- il existe une transition $(e,x,p) \longmapsto (e',q'')$,
alors, après application de cette transition, la nouvelle configuration de l'automate est $(e',w',q q')$ et la correspondance $(e,w,q) \vdash (e',w',q q')$ est appelée une dérivation valide dans l'automate.
Définition (Calcul valide)
Un calcul valide dans l'automate est une famille de dérivations $(e_1,w_1,q_1) \vdash (e_2,w_2,q_2) \vdash \vdash (e_n,w_n,q_n) $.
On dit que ce calcul valide mène de la configuration $(e_1,w_1,q_1) $ à la configuration $ (e_n,w_n,q_n) $
Notation: On peut noter cela : $(e_1,w_1,q_1) \stackrel{*}{\vdash} (e_n,w_n,q_n) $.
Définition (Mot reconnu)
On dit qu'un mot $w$ est reconnu par un automate à pile (état initial $e_0$, symbole de pile initial $p_0$) lorsqu'il existe un calcul valide $(e_0,w,q_0) \stackrel{*}{\vdash} (e,\varepsilon,q) $ tel que, au choix
- $e$ est un état d'acceptation : le mot $w$ est dit reconnu par l'état d'acceptation,
- $q$ est de la forme $q_sq'$ où $q_s \in Q$ : le mot $w$ est dit reconnu par symbole de sommet de pile,
- $q = \varepsilon$ (symbole de pile vide) : le mot $w$ est dit reconnu par pile vide,
Remarque : On peut envisager des reconnaissances par combinaison de deux de ces conditions, voire les trois simultanément.
On démontre que...
Théorème
Tous ces types de reconnaissance peuvent se ramener à la seule reconnaissance par pile vide (éventuellement avec un automate beaucoup plus compliqué ).
C'est pourquoi nous n'envisagerons plus que cette dernière dans la suite. Enfin,
Définition (Langage reconnu)
Le langage reconnu par automate est l'ensemble des mots reconnus par cet automate (par le même mode de reconnaissance).
Premiers exemples
Exemple :
Automate à pile (non déterministe) reconnaissant, par pile vide, l'ensemble des mots de la forme $ww^t$, concaténation de $w$ (constitué de 0 et de 1) et de son image miroir :

(Alphabet d'entrée $\{0,1\}$, fond de pile $Z$, alphabet de pile $\{Z,A,B\}$.)
Exemple :
Automate à pile reconnaissant, par pile vide, l'ensemble des mots de la forme $wcw^t$, concaténation de $w$ (constitué de 0 et de 1) et de son image miroir séparés par le caractère $c$ :
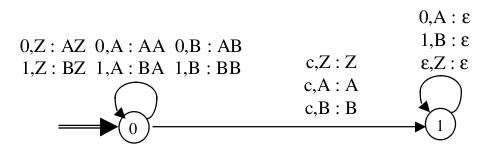
(Alphabet d'entrée $\{0,1,c\}$, fond de pile $Z$, alphabet de pile $\{Z,A,B\}$.)
Exemple plus complet : le langage $\{0^n 1^n | n \in \mathbb{N^*}\}$
Le principe est le suivant :
- Tant qu'on lit des 0, on les empile, sans changer d'état,
- Au premier 1 rencontré, on change d'état (pour ne plus accepter de 0),
- On dépile alors un à un les symboles de pile (sans jamais rien empiler),
- Si le mot se vide en même temps que la pile, il comportait autant de 0 que de 1.
Voici les transformations :
- $(e_0,0,p_0) \rightarrow (e_0,0)$
- $(e_0,0,0) \rightarrow (e_0,00)$
- $(e_0,1,0) \rightarrow (e_1,\varepsilon)$
- $(e_1,1,0) \rightarrow (e_1,\varepsilon)$
Exercice : Représentez cet automate.
Construction d'un automate à pile
Introduction à la méthode
On peut évidemment utiliser la méthode « directe\fg, comme dans l'exemple précédent.
Pour les langages plus complexes, il peut être nécessaire d'avoir recours à un algorithme. Nous l'aborderons par l'exemple de la grammaire écrite pour les expressions algébriques élémentaires :
| $<expression> $ | $ ::= $ | $ <terme>$ |
| $ | $ ::= $ | $ <terme> ~ '+' ~ <expression>$ |
| $<terme> $ | $::=$ | $ <facteur>$ |
| $ | $::=$ | $ <facteur> ~ '*' ~ <terme>$ |
| $<facteur> $ | $::=$ | $ ~ '(' ~ <expression> ~')'$ |
| $ | $ ::=$ | $ <variable>$ |
en omettant la définition du SNT « variable», inutile ici.
Utilisation d'un symbolisme
On introduit un nouveau symbolisme (développé dans la suite) pour cette même grammaire ; il se comprend aisément :
| $E $ | $ -> $ | $T$ |
| $E $ | $ -> $ | $T + E$ |
| $T $ | $ -> $ | $F$ |
| $T $ | $ -> $ | $F * T$ |
| $F $ | $ -> $ | $( E )$ |
| $F $ | $ -> $ | $a$ |
| $F $ | $ -> $ | $b$ |
| ... | ||
| $F $ | $ -> $ | $ z$ |
...en admettant comme symboles de variables les caractères alphabétiques minuscules.
Algorithme de construction
Le principe est de construire un automate à pile non déterministe qui admet des transitions vides :
- Au départ, sur une transition vide, on empile le SNT de l'axiome de la grammaire (ici, E) : c.f. transition (1).
- associer à chaque règle non terminale une $\epsilon$-transition qui empile les symboles de la partie droite (c.f. transitions (2) à (6))
- associer à chaque règle terminale $A \rightarrow x$ une transition $(e_0,x,A) \mapsto (e_0,\epsilon)$ (c.f.. transitions (7) et (8))
- associer à chaque symbole terminal une transition qui reconnaît ce symbole et dépile ce caractère (c.f. transitions (9) à (12))
On obtient les transitions suivantes :
| $(1) $ | $ (e_0,\varepsilon,p_0) $ | $\longmapsto $ | $(e_0,E)$ |
| $(2) $ | $ (e_0,\varepsilon,E) $ | $\longmapsto $ | $(e_0,T)$ |
| $(3) $ | $ (e_0,\varepsilon,E) $ | $\longmapsto $ | $(e_0,T+E)$ |
| $(4) $ | $ (e_0,\varepsilon,T) $ | $\longmapsto $ | $(e_0,F)$ |
| $(5) $ | $ (e_0,\varepsilon,T) $ | $\longmapsto $ | $(e_0,F*T)$ |
| $(6) $ | $ (e_0,\varepsilon,F) $ | $\longmapsto $ | $(e_0,(E))$ |
| $(7) $ | $ (e_0,a,F) $ | $\longmapsto $ | $(e_0,\varepsilon)$ |
| $\vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| $(8) $ | $ (e_0,z,F) $ | $\longmapsto $ | $(e_0,\varepsilon)$ |
| $(9) $ | $ (e_0,+,+) $ | $\longmapsto $ | $(e_0,\varepsilon)$ |
| $(10) $ | $ (e_0,*,*) $ | $\longmapsto $ | $ (e_0,\varepsilon)$ |
| $(11) $ | $ (e_0,(,() $ | $\longmapsto $ | $ (e_0,\varepsilon)$ |
| $(12) $ | $ (e_0,),)) $ | $\longmapsto $ | $ (e_0,\varepsilon)$ |
Exercices
Exercice : Soit l'automate à pile défini par $\Sigma=\{a,b\}$, $E=\{q_0,q_1,q_2\}$, $P=\{p_, A\}$ et les transitions suivantes
$(q_0,a,p_0) \mapsto (q_1,A) $
$(q_1,b,A) \mapsto (q_2,\epsilon)$
$(q_1,a,p) \mapsto (q_1,Ap)$
$(q_2,b,A) \mapsto (q_2,\epsilon)$
- Donner les enchaînements des transitions permettant d'accepter $aabb$ en précisant s'il y a des points de non déterminisme dans la dérivation.
- Donner l'enchaînement des transitions conduisant à l'échec de l'acceptation de la chaîne $aaba$.
- Décrire l'état de l'automate après avoir lu $n$ symboles $a$ en entrée $(n \in \mathbb{N})$. Quelle est alors la seule façon de vider la pile ? En déduire le langage reconnu par cet automate à pile avec arrêt sur pile vide.
Exercice : Pour $u \in \Sigma^*$ , on note $|u|_a$ le nombre de $a$ dans $u$ et $|u|_b$ le nombre de $b$ dans $u$.
Donner un automate à pile qui reconnaît $L = \{u \in \Sigma^*, |u|_a = |u|_b \}$.
Exercice : Soit $\Sigma = \{0, 1\}$. Donner un automate à pile qui accepte un mot $u \in \Sigma^*$ ssi aucun préfixe de $u$ ne contient plus de 1 que de 0. Préciser si l’automate est déterministe.
Exercice : Soit $\Sigma = \{1, 2\}$. Donner un automate à pile qui reconnaît le langage suivant : $\{1^n 2^n | n \geqslant 0\}\cup \{1^n 2^{2n} | n \geqslant 0\}$ Préciser si l’automate est déterministe.
Exercice : Soit $\Sigma = \{a, b, c\}$. Donner un automate à pile qui reconnaît le langage suivant : $\{a^i b^j c^k | i = j \textrm{ ou } j = k\}$ Préciser si l’automate est déterministe.
Exercice : Soit $G$ la grammaire suivante : $S \rightarrow aAB ~~~ A \rightarrow aAB | a ~~~ B \rightarrow bBA | aC ~~~ C \rightarrow BaA.$
- Donner des exemples de mots reconnus.
- Donner un automate à pile qui reconnaît le langage généré par la grammaire $G$.
Exercice : Soit $G$ la grammaire suivante : $S \rightarrow aAB ~~~ A \rightarrow aAB | a ~~~ B \rightarrow bBA | aC | b ~~~ C \rightarrow BaA.$ Donner un automate à pile qui reconnaît le langage généré par la grammaire $G$.