Texte : en pdf.

Introduction

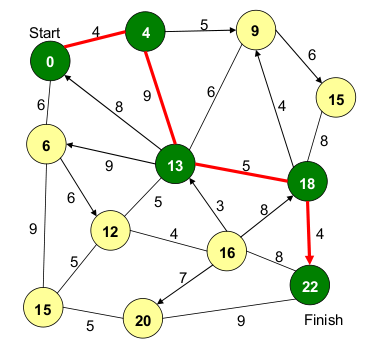
Dans l'épisode 23 de la saison 3 de Numb3rs, intitulé Money for Nothing, un camion contenant de l'argent et des médicaments a été attaqué.

Comme les voleurs souhaitent quitter la ville (Los Angeles) le plus rapidement possible, et qu'ils ont prémédité leur coup, le héros (Charlie) essaye de déterminer le plus rapide des chemins possibles, reliant le lieu de l'embuscade à la porte de sortie de la ville la plus proche.

L'embuscade a eu lieu dans le noeud (croisement) supérieur gauche de l'image ci-dessous, et la sortie est le noeur inférieur droit ;

• une flèche représente une rue à sens unique,
• un arc représente une rue empruntable dans les deux sens.

Les valeurs sur les arcs/flèches représentent les temps nécessaires pour rejoindre chaque croisement.

Tester toutes les solutions devient vite inextricable. L'idée est alors d'utiliser un algorithme de recherche du plus court chemin : Dijkstra.

Il y a deux solutions possibles, elles sont indiquées sur le schéma en vert.

Vers une résolution networkx du problème

On importe le module networks, et on crée un graphe orienté :

  >>> from networkx import *
  >>> G=MultiDiGraph()

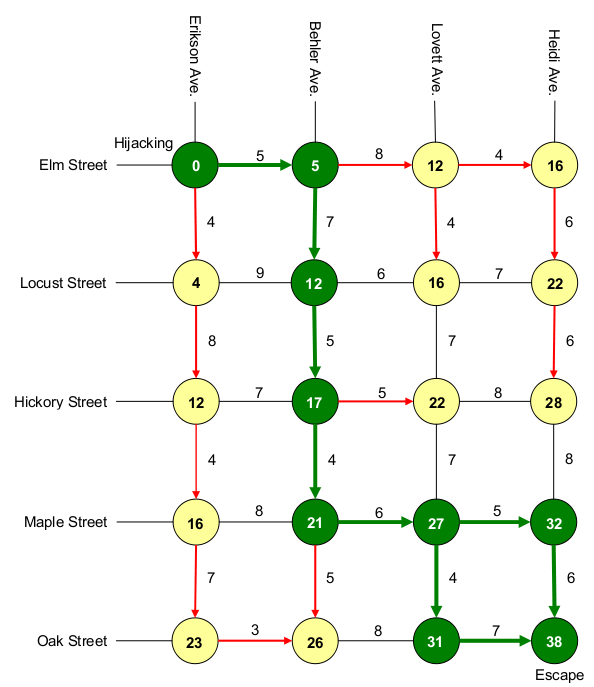
On commence par saisir les 20 noeuds dans une liste. Par exemple, le noeud correspondant au croisement des rues Maple Street et Behler Ave., numéroté 21 sur le dessin, correspond à l'élément (1,3) dans notre liste (le point (0,0) est le noeud supérieur gauche, lieu de l'attaque).

  >>> L=[]
  >>> for x in range(4):
  ...     for y in range(5):
  ...         L.append((x,y))
  ... 

On ajoute cette liste de noeuds à notre digraphe :

  >>> G.add_nodes_from(L)

Il faut maintenant mettre les poids sur les flèches, c'est-à-dire mettre le temps nécessaire à rejoindre deux croisements adjacents. C'est un peu long, mais bon...

  >>> G.add_edge((0,0),(1,0),5)
  >>> G.add_edge((1,0),(2,0),8)
  >>> G.add_edge((2,0),(3,0),4)
  >>> G.add_edge((0,0),(0,1),4)
  >>> G.add_edge((1,0),(1,1),7)
  >>> G.add_edge((2,0),(2,1),4)
  >>> G.add_edge((3,0),(3,1),6)
  >>> G.add_edge((0,1),(1,1),9)
  >>> G.add_edge((1,1),(2,1),6)
  >>> G.add_edge((2,1),(3,1),7)
  >>> G.add_edge((0,1),(0,2),8)
  >>> G.add_edge((1,1),(1,2),5)
  >>> G.add_edge((2,1),(2,2),7)
  >>> G.add_edge((3,1),(3,2),6)
  >>> G.add_edge((0,2),(1,2),7)
  >>> G.add_edge((1,2),(2,2),5)
  >>> G.add_edge((2,2),(3,2),8)
  >>> G.add_edge((0,2),(0,3),4)
  >>> G.add_edge((1,2),(1,3),4)
  >>> G.add_edge((2,2),(2,3),7)
  >>> G.add_edge((3,2),(3,3),8)
  >>> G.add_edge((0,3),(1,3),8)
  >>> G.add_edge((1,3),(2,3),6)
  >>> G.add_edge((2,3),(3,3),5)
  >>> G.add_edge((0,3),(0,4),7)
  >>> G.add_edge((1,3),(1,4),5)
  >>> G.add_edge((2,3),(2,4),4)
  >>> G.add_edge((3,3),(3,4),6)
  >>> G.add_edge((0,4),(1,4),3)
  >>> G.add_edge((1,4),(2,4),8)
  >>> G.add_edge((2,4),(3,4),7)

Astuce : Ne recopiez pas ce qui précède, ligne par ligne. Faites un copier-coller dans un éditeur, et remplacez tous les >>> par rien du tout.

Travaux pratiques

On a, dans ce qui précède, supposé que toutes les rues étaient à sens unique. Rajoutez des arcs orientés au graphe G pour coller exactement au problème de Charlie.

Il reste maintenant à réfléchir à un algorithme trouvant le plus court chemin. Une étude systématique de tous les chemins possibles n'étant évidemment pas envisageable, on va s'orienter vers des algorithmes évolués de recherche de plus court chemin.

L'algorithme de Floyd

Présentation

L'algorithme de Floyd est un premier algorithme, naïf, permettant de répondre au problème de la recherche de plus court chemin. Il est simple, mais coûteux.

Remarques préliminaires

Il faut d'abord qu'un plus court chemin existe, donc supposer les graphes :

• connexes, (il existe bien un chemin entre les sommets considérés)
• à poids positifs (sans cela, l'existence d'un chemin minimal n'est pas assuré).

Description de l'algorithme

Fondements

Il y a, à la base de l'algorithme, les remarques suivantes :

• si $(a_0,...,a_i,...,a_p)$ est un plus court chemin de $a_0$ à $a_p$, alors :
  • $(a_0,...,a_i)$ est un plus court chemin de $a_0$ à $a_i$,
  • $(a_i,...,a_p)$ est un plus court chemin de $a_i$ à $a_p$.
• Les poids des arêtes étant positives, tout chemin contenant un cycle est nécessairement plus long que le même chemin sans le cycle. On peut, de ce fait, se limiter à la recherche de plus courts chemins passant par des sommets deux à deux distincts.

Matrice M des distances

La suite de matrices $M^k$ est initialisée par la matrice $M^0$, de taille $n\times n$ (où $n$ est le nombre de sommets du graphe), telle que

• $M_{i,j}^0 = k$ s'il existe un arc de poids $k$ entre $i$ et $j$,
• $M_{i,j}^0 = +\infty$ sinon.

Il suffit ensuite de calculer la suite de matrices $M^(k), k \gesqlant 1$ définies par :

$M_{i,j}^{k}=min \left(M_{i,j}^{k-1},M_{i,k}^{k-1} + M_{k,j}^{k-1}\right)$

C'est-à-dire...

• $M^1$ vaut :

$\left( \begin{array}{cccc} \min{\left(M_{1,1}^0,M_{1,1}^0 + M_{1,1}^0\right)} & \min{\left(M_{1,2}^0,M_{1,1}^0 + M_{1,2}^0\right)} & ... & \min{\left(M_{1,n}^0,M_{1,1}^0 + M_{1,n}^0\right)}\\ \min{\left(M_{2,1}^0,M_{2,1}^0 + M_{1,1}^0\right)} & \min{\left(M_{2,2}^0,M_{2,1}^0 + M_{1,2}^0\right)} & ... & \min{\left(M_{2,n}^0,M_{2,1}^0 + M_{1,n}^0\right)} \\ \min{\left(M_{3,1}^0,M_{3,1}^0 + M_{1,1}^0\right)} & \min{\left(M_{3,2}^0,M_{3,1}^0 + M_{1,2}^0\right)} & ... & \min{\left(M_{3,n}^0,M_{3,1}^0 + M_{1,n}^0\right)} \\ \vdots & \vdots & ... & \vdots \\ \min{\left(M_{n,1}^0,M_{n,1}^0 + M_{1,1}^0\right)} & \min{\left(M_{n,2}^0,M_{n,1}^0 + M_{1,2}^0\right)} & ... & \min{\left(M_{n,n}^0,M_{n,1}^0 + M_{1,n}^0\right)} \end{array}\right)$

• $M^2$ vaut :

$\left( \begin{array}{cccc} \min{\left(M_{1,1}^1,M_{1,2}^1 + M_{2,1}^1\right)} & \min{\left(M_{1,2}^1,M_{1,2}^1 + M_{2,2}^1\right)} & ... & \min{\left(M_{1,n}^1,M_{1,2}^1 + M_{2,n}^1\right)}\\ \min{\left(M_{2,1}^1,M_{2,2}^1 + M_{2,1}^1\right)} & \min{\left(M_{2,2}^1,M_{2,2}^1 + M_{2,2}^1\right)} & ... & \min{\left(M_{2,n}^1,M_{2,2}^1 + M_{2,n}^1\right)} \\ \min{\left(M_{3,1}^1,M_{3,2}^1 + M_{2,1}^1\right)} & \min{\left(M_{3,2}^1,M_{3,2}^1 + M_{2,2}^1\right)} & ... & \min{\left(M_{3,n}^1,M_{3,2}^1 + M_{2,n}^1\right)} \\ \vdots & \vdots & ... & \vdots \\ \min{\left(M_{n,1}^1,M_{n,2}^1 + M_{2,1}^1\right)} & \min{\left(M_{n,2}^1,M_{n,2}^1 + M_{2,2}^1\right)} & ... & \min{\left(M_{n,n}^1,M_{n,2}^1 + M_{2,n}^1\right)} \end{array}\right)$

• Et ainsi de suite...

En effet,pour $k>0$, $M_{i,j}^{k}$ est la longueur du plus court chemin entre $i$ et $j$, en ne considérant que les sommets intermédiaires $0,1,...,k$.

Ainsi, après $n$ calculs, on obtient la matrice des longueurs des plus courts chemins.

Matrice P des poids

Exemple

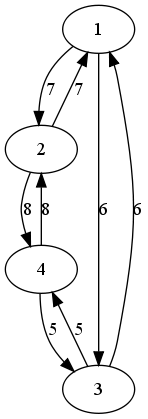
On souhaite appliquer l'algorithme de Floyd-Warshall au graphe :

Initialisation

• On initialise notre suite de matrices par les distances contenues dans le graphe, en mettant $\infty$ s'il n'y a pas d'arêtes entre les sommets concernés :

$M^0 = \left(\begin{array}{cccc} 0 & 7 & 6 & \infty \\ 7 & 0 & \infty & 8 \\ 6 & \infty & 0 & 5 \\ \infty & 8 & 5 & 0 \end{array}\right)$

• La première matrice des prédécesseurs contient :
  • $None$ s'il n'y a pas d'arêtes menant de $i$ à $j$,
  • $i$ si $i = j$,
  • $i$ s'il existe une arête de $i$ à $j \neq i$.

$P^0 = \left(\begin{array}{cccc} 1 & 1 & 1 & None \\ 2 & 2 & None & 2 \\ 3 & None & 3 & 3 \\ None & 4 & 4 & 4 \end{array}\right)$

Deuxième étape

• Pour déterminer l'élément $(i,j)$ de $M^1$, on prend la plus petite valeur entre $M_{i,j}^0$ et $M_{i,1}^0$ et $M_{1,j}^0$...

$M^1 = \left(\begin{array}{cccc} 0 & 7 & 6 & \infty \\ 7 & 0 & 13 & 8 \\ 6 & 13 & 0 & 5 \\ \infty & 8 & 5 & 0 \end{array}\right)$

• À la base, $P^1 = P^0$, et à chaque fois qu'un élément $(i,j)$ a été modifié dans $M^1$, on met 1 en position $(i,j)$ dans $P^1$.

$P^1 = \left(\begin{array}{cccc} 1 & 1 & 1 & None \\ 2 & 2 & 1 & 2 \\ 3 & 1 & 3 & 3 \\ None & 4 & 4 & 4 \end{array}\right)$

Troisième étape

• Pour déterminer l'élément $(i,j)$ de $M^2$, on prend la plus petite valeur entre $M_{i,j}^1$ et $M_{i,2}^1$ et $M_{2,j}^1$.

$M^2 = \left(\begin{array}{cccc} 0 & 7 & 6 & 15 \\ 7 & 0 & 13 & 8 \\ 6 & 13 & 0 & 5 \\ 15 & 8 & 5 & 0 \end{array}\right)$

• On part de $P^2 = P^1$, et à chaque fois qu'un élément $(i,j)$ a été modifié dans $M^2$, on met 2 en position $(i,j)$ dans $P^2$. Cela donne :

$P^2 = \left(\begin{array}{cccc} 1 & 1 & 1 & 2 \\ 2 & 2 & 1 & 2 \\ 3 & 1 & 3 & 3 \\ 2 & 4 & 4 & 4 \end{array}\right)$

Quatrième étape

• On poursuit l'algorithme : $M_{i,j}^3 = Min(M_{i,3}^2;M_{3,j}^2$ :

$M^3 = \left(\begin{array}{cccc} 0 & 7 & 6 & 11 \\ 7 & 0 & 13 & 8 \\ 6 & 13 & 0 & 5 \\ 11 & 8 & 5 & 0 \end{array}\right)$

• De même,

$P^3 = \left(\begin{array}{cccc} 1 & 1 & 1 & 3 \\ 2 & 2 & 1 & 2 \\ 3 & 1 & 3 & 3 \\ 3 & 4 & 4 & 4 \end{array}\right)$

Dernière étape

Il nous reste un dernier sommet à envisager : le 4. On ne trouve aucun changement...

$M^4 = \left(\begin{array}{cccc} 0 & 7 & 6 & 11 \\ 7 & 0 & 13 & 8 \\ 6 & 13 & 0 & 5 \\ 11 & 8 & 5 & 0 \end{array}\right) P^4 = \left(\begin{array}{cccc} 1 & 1 & 1 & 3 \\ 2 & 2 & 1 & 2 \\ 3 & 1 & 3 & 3 \\ 3 & 4 & 4 & 4 \end{array}\right)$

Exploitation des résultats

Evaluation de l'algorithme

1. Chaque matrice se calculant en $O(n^2)$, l'algorithme final est en $O(n^3)$ opérations (et $O(n^2)$ en espace). On verra que Dijkstra sera meilleur.
2. Cet algorithme fournit tous les poids des chemins les plus courts.
3. Cependant, pour déterminer ces chemins, il faut une autre suite de matrices, contenant en position $(i,j)$ le sommet $k$ par lequel il faut passer dans un chemin le plus court de $i$ à $j$ : par appel récursif, on pourra reconstruire le chemin proprement dit (ce qui engendre un coût supplémentaire).
4. Enfin, cet algorithme est plus approprié pour les graphes denses.

Résolution du problème de Charlie

Le module networkx possède une méthode permettant d'appliquer l'algorithme de Floyd à notre graphe. Cette méthode s'appelle path.floyd_warshall :

  >>> path.floyd_warshall(G)
  ({(0, 1): {(0, 1): 0, (1, 2): 14, (3, 2): 27, (0, 0): inf, 
    (3, 3): 29, (3, 0): inf, (2, 4): 28, (3, 1): 22, (1, 4): 22,
    (0, 2): 8, (2, 0): inf, (1, 3): 18, (2, 3): 24, (2, 1): 15, ...

Le retour semble assez compliqué. En fait, on retrouve les deux éléments renvoyés par l'algorithme de Floyd : la distance, et le chemin (un couple de dictionnaires)...

  >>> (distance, chemin)=path.floyd_warshall(G)
  >>> distance[(0,1)]

On trouve les distances du sommet (0,1) à tous les autres sommets :

• à lui-même (0,1), la distance est nulle,
• au sommet (1,2), la distance vaut 14,
• etc.

On peut aussi préciser le sommet d'arrivée qui nous intéresse :

  >>> distance[(0,1)][(1,1)]
  9

On peut donc trouver le temps (distance) du plus court chemin entre notre lieu d'attaque, et la sortie de la ville :

  >>> distance[(0,0)][(3,4)]
  38

Il reste à obtenir ce chemin. On se souvient que, dans l'algorithme ci-dessus, la matrice des chemins doit être remontée récursivement. Ainsi,

  >>> chemin[(0,0)][(3,4)]
  (3, 3)

signifie que, quand on emprunte le plus court chemin entre le croisement (0,0) et le croisement (3,4), le dernier croisement visité est (3,3).

On peut recommencer pour trouver le plus court chemin entre (0,0) et (3,3) - on connaît la fin du parcours :

  >>> chemin[(0,0)][(3,3)]
  (2, 3)

On continue ainsi, récursivement :

  >>> chemin[(0,0)][(2,3)]
  (1, 3)
  >>> chemin[(0,0)][(1,3)]
  (1, 2)
  >>> chemin[(0,0)][(1,2)]
  (1, 1)
  >>> chemin[(0,0)][(1,1)]
  (1, 0)
  >>> chemin[(0,0)][(1,0)]
  (0, 0)

On retrouve bien le chemin indiqué en vert. Connaissant le moment de l'attaque, on sait donc à quel carrefour se placer pour avoir le plus de chances de retrouver les agresseurs.

Travaux pratiques

1. Réalisez l'algorithme de Floyd. On utilisera networkx pour le graphe, et numpy pour les matrices.
2. L'appliquer à l'exemple précédent.
3. Faire de même avec :