WikiMath

Définition de la fonction logistique

Introduction

On présente maitenant une autre fonction, dont les itérées se comportent comme la bifurcation de Feigenbaum. C'est la fonction logistique, célèbre exemple de chaos.

On peut remarquer que la fonction logistique n'est rien d'autre qu'une réécriture du modèle de Verhulst.

Définition

La fonction logistique est définie par $\forall x \in [0,1], f(x)=ax(1-x)$ où $a$ est un paramètre choisi dans le segment [0,4].

On s'intéresse au système dynamique $u_0 \in [0;1], u_{n+1} = f(u_n)$

que l'on peut représenter graphiquement...

Représentation graphique de la fonction logistique

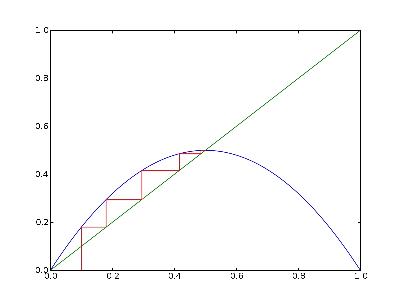
Il n'y a pas divergence de la suite, pour ces valeurs initiales choisies.

Comportement de la suite

Convergence de la suite

La suite se comporte différemment selon la valeur du paramètre $a$ : pour $a<3$, la suite converge.

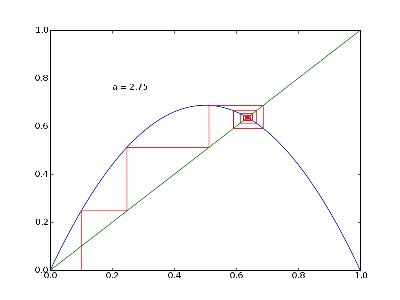
2-cycle

Pour a légèrement supérieur à 3, le point stable de f n'est plus attractif.

Il apparaît un 2-cycle (deux points stables pour fof, en plus de celui de f), donc une orbite périodique.

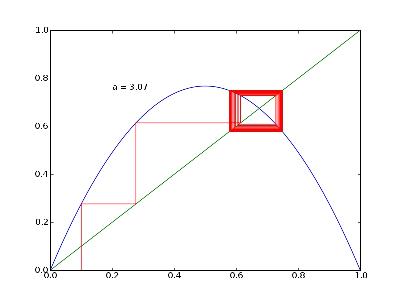
4-cycle, 8-cycle, etc.

En augmentant la valeur de a, on obtient des orbites de période 4, puis 8, etc.

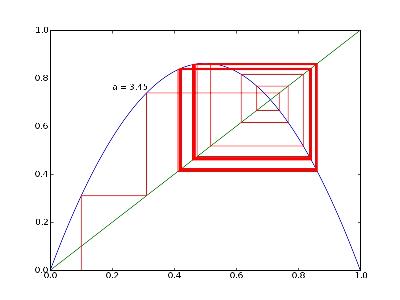
a=3,56

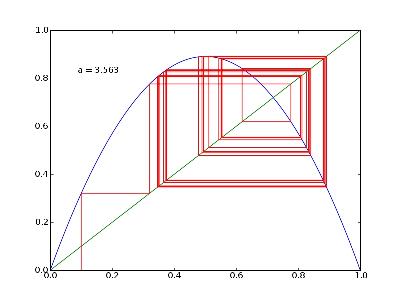
Caractère erratique

Pour $a\simeq 3,86$, l'orbite présente un caractère erratique, complètement différent des modèles précédents qui étaient prédictibles :

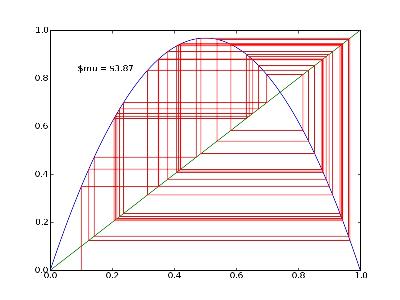
Sensibilité aux conditions initiales

Pour deux valeurs différentes de 0,1%, les résultats obtenus après 25 itérations diffèrent de 80% :

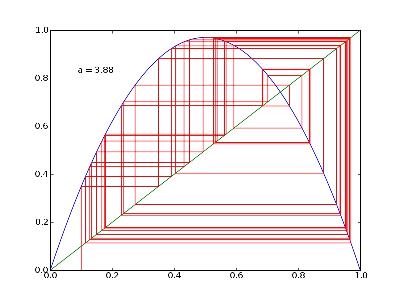
a=3,90

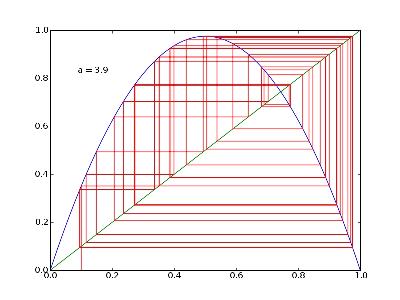
Le chaos dans tout ça ?

Le chaos

La suite logistique est pleinement connue, facilement définissable (totalement déterministes), pourtant son comportement n'est pas prévisible.

Plus exactement, une infime variation de la valeur initiale, et le système peut passer d'une convergence à un comportement périodique, ou d'un comportement périodique à un comportement aléatoire : c'est l'effet papillon.

Exemple célèbre de chaos

Reprenons l'exemple de la météorologie : le temps qu'il fera demain se détermine à partir des conditions climatiques d'aujourd'hui.

Or, on ne peut pas mesurer, avec une précision suffisamment poussée, les conditions climatiques actuelles.

Mais la météorologie est un système chaotique, donc une légère erreur sur les données actuelles peut donner des prévisions complètement différentes...

Programme Python traçant la fonction logistique

Pour lancer ce programme, il faut le module python-matplotlib installé.

Dans un terminal, n'oubliez pas de passer en argument la valeur du paramètre a, et le point de départ de la suite (si votre programme s'appelle logistic.py, alors lancez-le ainsi : python logistic.py 3.1 0.1 par exemple).

Le programme

  from pylab import *
  from os import system
  import sys
  X=arange(0,1,0.001)
  a=float(sys.argv[1])

  def f(t):
      return a*t*(1-t)

  Y=f(X)
  x0=float(sys.argv[2])
  x,y=[x0,x0],[0,f(x0)]

  for k in range(40):
      x.append(y[len(y)-1])
      y.append(x[len(x)-1])
      x.append(y[len(y)-1])
      y.append(f(x[len(x)-1]))

  text(0.09,0.82,'a = '+str(a))
  plot(X,Y,X,X,x,y)

  savefig('foncLogicstr(int(100*a)).png', dpi=100)