WikiMath

Présentation de la méthode

La résolution de l'équation

$f(x) = 0$

peut se ramener à la résolution d'un autre problème mathématique connu, à savoir la recherche d'un point fixe. C’est-à-dire la résolution de l’équation

$x = g (x)$,

sous réserve que ces deux formulations soient mathématiquement équivalentes.

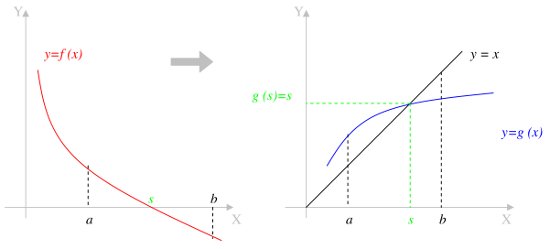
Dans l'illustration ci-dessus, plutôt que de rechercher le point $s$ annulant $f$ (partie gauche), on va

• rechercher une fonction $g$ dont $s$ est un point fixe ($g(s)=s$, graphe de droite),
• appliquer une méthode de point fixe à $g$ :

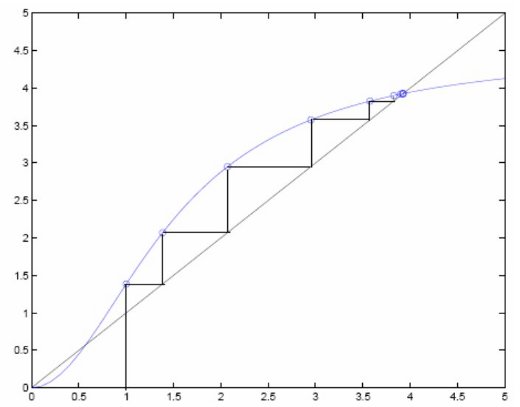
Comme $s$ est la même valeur dans les deux cas, on a la solution du problème de départ.

L'utilité de ce changement de problème est que la recherche d'un point fixe est relativement simple à programmer. Cependant, la convergence n'est garantie que sous certaines conditions.

La méthode du point fixe

Réaliser la méthode du point fixe revient à effectuer dans l'ordre les points suivants.

• Déterminer un intervalle [$a, b$] contenant une unique solution pour l'équation $f(x) = 0$.
• Transformer l'équation $f(x) = 0$ en une équation du type $x = g(x)$ :

• Choisir $x_0$ dans l’intervalle [$a, b$].
• Calculer la solution approchée recherchée, en itérant la formule

$x_{n+1} = g(x_n)$

Travaux pratiques

Dans ce qui suit, on souhaite retrouver la racine de $f(x) = x^3-x-1$ dans [1,2], en se ramenant à une méthode du point fixe.

On propose de prendre tour à tour pour $g$ chacune des fonctions suivantes :

1. $g(x) = x^3-1$,
2. $g(x) = \frac{1}{x^2-1}$,
3. $g(x) = (x+1)^{1/3}$ : la racine cubique de $x+1$.

On vous demande de faire :

1. Regarder si ces fonctions vérifient les propriétés nécessaires à la convergence de la méthode :
   • Regarder si $f(x)=0$ est équivalent à $g(x)=x$.
   • Vérifier que $g$ est continue et dérivable sur [1,2].
   • Regarder si $g($ [1,2]) est bien inclus dans [1,2].
   • Vérifier, enfin, que $g'(x)<1$ sur [1,2].
2. Si tel est le cas...
   • Faire tourner la méthode pour trouver la racine de $f$ à $10^{-3}$, et $10^{-5}$ près.
   • Comparer vos résultats (rapidité de convergence, etc.) aux méthodes précédemment exposées.
   • Quelle méthode vous semble la meilleure ?