WikiMath

Présentation de la méthode

A l’instar de la méthode de dichotomie, la méthode de Lagrange (appelée aussi méthode de la fausse position ou méthode des parties proportionnelles) permet de trouver une bonne approximation de la solution de l’équation

$f(x) = 0$

sur un intervalle [$a, b$], cette solution étant déterminée à $\epsilon$ près.

La différence entre les deux méthodes réside dans la façon dont on réduit la longueur de l'intervalle encadrant la solution cherchée. Dans la méthode de Lagrange, on ne coupera pas l’intervalle en deux parties égales.

La méthode de Lagrange

La méthode de Lagrange consiste à répéter les points suivants, le nombre de fois qu'il faut.

• Encadrer la solution cherchée.

• Réduire la longueur de l’intervalle contenant la solution cherchée.

$c = \frac{a \times f(b) - b \times f(a )}{f(b) - f(a)}$

• Un seul des trois cas suivants est possible :
  • $f(a) \times f (c) = 0$ (à $\epsilon$ près), alors $c$ est la solution.
  • $f(a) \times f(c) < 0$, alors la solution est dans l’intervalle [$a, c$].
  • $f(a) \times f (c) > 0$, auquel cas la solution est dans l’intervalle [$c, b$].
• Recommencer ce qui précède autant de fois que nécessaire.

Nous réduisons, à chaque itération, la longueur de l'intervalle contenant la solution recherchée.

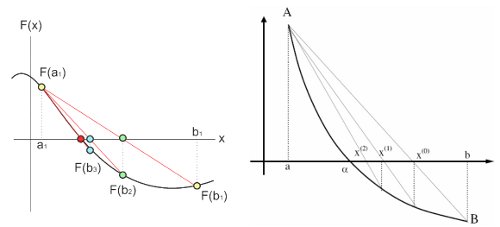
On itère le processus jusqu'à ce que la longueur de l’intervalle obtenu soit assez petite pour donner la solution à la précision recherchée.

Travaux pratiques

1. Trouver la racine de la fonction $f(x) = x^3-x-1$, à $10^{-3}$ et $10^{-5}$ près, par la méthode de Lagrange.
2. Faire une fonction lagrange, qui reçoit la fonction et l'intervalle de départ, ainsi que la condition d'arrêt, et qui renvoie la racine recherchée.
3. Comparer la méthode de Lagrange à la recherche dichotomique, sur divers exemples.
   • Pour un nombre d'itérations donné, obtient-on dans les deux cas la même précision ?
   • Pour une précision voulue, a-t-on un même nombre d'itérations ?
   • Les coûts (opérations élémentaires, temps de calcul) pour une itération sont les mêmes dans les deux méthodes ?

On cherchera à prévoir (en théorie) les réponses à ces questions, puis à vérifier ses prévisions expérimentalement. (Solution.)

Si vous êtes suffisamment en avance, vous pouvez tenter de moyenner un grand nombre de résultats, et penser à utiliser les modules PyX et timeit, pour produire des graphes et mesurer précisément les temps de calcul expérimentaux (voir l'aide sur ces modules contenu dans ce wiki).