WikiMath

Modèle Général d'un neurone artificiel

Le modèle général de neurone artificiel comporte cinq composants:

• Un ensemble d'entrées, $x_1, \ldots, x_n$
• Un ensemble de poids, $w_1, \ldots, w_n$
• Un biais $b$
• Une fonction de transfert $f$
• une sortie $s$

Production du neurone

Le neurone calcule sa sortie $s$ grâce à l'équation suivante

$ f(\Sigma_{i=0}^{n-1} w_i.x_i -b) = f(\Sigma_{i=0}^{n} w_i.x_i)$ ou $w_n$ est égal à $b$ et $x_n$ à $-1$.

Cette sortie peut être passée en entrée à un groupe de neurones ou transmise directement à l'environnement extérieur.

Travaux pratiques : développement du neurone

1. Développer un neurone avec les cinq attributs énoncés ci-dessus et un constructeur permettant de les fixer. La sortie sera calculée.
2. Instancier un neurone à deux entrées $x_1$ et $x_2$ et la fonction binaire comme fonction d'activation. A l'aide d'essais successifs, déterminer les poids $w_1$, $w_2$ et le biais $b$ de sorte que le neurone calcule la sortie adéquate selon le tableau suivant :

$x_1$	$x_2$	Sortie
-0,2	0,5	0
0,2	-0,5	0
0,8	-0,8	1
0,8	0,8	1

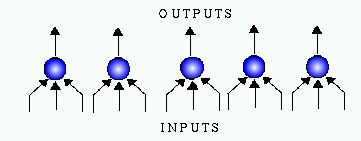
Réseau de neurones : perceptron simple couche

Un perceptron simple couche consiste en un ou plusieurs neurones artificiels en parallèle : chaque neurone fourni une sortie qui est connecté au monde extérieur.

Apprentissage dans un perceptron simple couche : règle delta

Cet algorithme d'apprentissage du perceptron a été développé par Frank Rosenblatt à la fin des années 50. Son but est de faire évoluer le réseau vers celui qui minimise les erreurs commises sur l'ensemble des exemples. Il est le suivant:

1. Initialisation des poids et biais ($w_{0}$, $\ldots$, $w_{n-1}$, $w_n$) à des valeurs aléatoires comprises entre 0 et 1.
2. Présentation du motif d'apprentissage $x$ donné en entrée du neurone et calcul de la sortie.
3. Les poids $w$ sont modifiés comme suit $ w(t+1)=w(t)+\eta.(d-s).x$ où
   • $w$ est le poids,
   • $d$ est la sortie théorique,
   • $s$ est la sortie réelle,
   • $x$ est l'entrée,
   • $\eta$ est un coefficient d'apprentissage (entre 0 et 1) (que l'on peut diminuer au cours de l'apprentissage).
4. Répétition des étapes 2 et 3 jusqu'à ce que :
   • l'erreur de l'itération ($E = 1/2.(s -d)^2$) est inférieure à un seuil d'erreur spécifié par l'utilisateur.
   • un nombre d'itérations prédéterminé s'est écoulé.

Travaux pratiques :

1. Implanter la règle du delta et l'appliquer sur l'exemple de la page précédente

Projet à réaliser en binome pour le 01 avril 2010 à 0h00

1. Concevoir un réseau de 144 neuronnes, chacun à 144 entrées
2. Lui faire apprendre les caractères numériques (0-9)
3. Le tester sur sur des versions dégradées de ces caractères
4. Lui ajouter les voyelles minuscules de l'alphabet.
5. Le tester sur des versions dégradées de ces voyelles
6. Sont à fournir :
   1. Tout le code python
   2. Toutes les données d'apprentissage
   3. Toues les données d'essai.
   4. Un rapport de 2 pages synthétisant l'originalité du développement.