WikiMath

---

Mémoires auto-associatives

Présentation

Dans la désignation mémoire associative,le terme mémoire fait référence à la fonction de stockage de ces réseaux, et le terme associative au mode d’adressage, puisque qu’il faut fournir de l’information au réseau pour obtenir celle qui est mémorisée : c’est une mémoire adressable par son contenu.

Avec les mémoires auto-associatives, il faut fournir une partie de l’information stockée pour obtenir l’information stockée (par exemple : partie du visage pour obtenir le visage en entier).

Les applications de ces mémoires sont essentiellement la reconstruction de signaux et leur reconnaissance.

Structure

Chaque neurone est relié à tous les autres, et à toutes les entrées. La fonction de transfert est habituellement l’identité.

L'évaluation peut se faire de manière synchrone (toutes les unités évoluent en même temps) ou asynchrone (les éléments du réseaux évoluent les uns après les autres).

Apprentissage

L'apprentissage est de type supervisé.

C'est-à-dire que la base d’apprentissage est constituée de couples de vecteurs entrée et sortie associés, et est basé sur la règle de Hebb.

Exemple : le modèle de Hopfield

Le modèle de Hopfield est une mémoire auto-associative.

La réponse des neurones est asynchrone, et les neurones ont pour fonction de transfert la fonction signe : la réponse est binaire.

Il est possible réaliser l'apprentissage par un calcul direct à partir des exemples à mémoriser grâce à la règle de Hebb généralisée.

Mémoires hétéro-associatives et cartes topologiques de Kohonen

Présentation

Avec les mémoires hétéro-associatives, on fournit une information au réseau et celui-ci rend une information différente. Par exemple, un visage donne un nom.

Chaque neurone est relié à toutes les entrées, mais les neurones ne sont pas reliés entre eux. La fonction de transfert est linéaire.

Diverses méthodes peuvent être utilisées, comme la règle de Hebb ou la règle du delta.

Applications

Les mémoires à apprentissage supervisé sont principalement utilisées pour la mémorisation et la reconnaissance de formes. Par exemple, associer le nom d'une lettre à l'image de la lettre.

Les réseaux à apprentissage non supervisés sont en revanche utilisés pour des fonctions de classification et d'agrégation (clustering).

Exemple : les cartes auto-organisatrices de Kohonen.

Kohonen s'est inspiré de la topologie de certaines zones du cortex qui présentent la même organisation que les capteurs sensoriels.

Des zones proches correspondent à des neurones proches dans le cortex. Tous les neurones sont interconnectés, mais seuls les neurones proches ont de l'influence, selon une fonction DOG (Difference Of Gaussian) en forme de cloche.

Les neurones les plus proches sont excitateurs, ceux un peu plus éloignés inhibiteur et les plus éloignés ont une influence nulle.

La fonction d'entrée est de type sigmoïde, et le réseau présente la particularité de n'avoir qu'un seul neurone actif à la fois.

Il réalise une tâche de classification : des entrées aux caractéristiques proches donnent une même sortie.

Les réseaux multicouches (non bouclés)

Présentation

Les MLP (multi-layer perceptron), ou réseaux à couches, forment la très grande majorité des réseaux. Ils sont intemporels (ce sont des réseaux statiques et non dynamiques).

Les neurones sont organisés en couches : chaque neurone est connecté à toutes les sorties des neurones de la couche précédente, et nourrit de sa sortie tous les neurones de la couche suivante. Ces réseaux sont d'ailleurs qualifiés de feedforward en anglais : nourrit devant.

Pour la première couche ses entrées sont l'entrée du réseau. Une couche est souvent rajoutée pour constituer les entrées, appelée couche d'entrée - mais elle n'en est pas une puisqu'elle ne réalise aucun traitement.

Les fonctions d'entrée et de transfert sont les mêmes pour les neurones d'une même couche, mais peuvent différer selon la couche.

Ainsi la fonction de transfert de la couche de sortie est généralement l'identité.

Représentation

Un réseau à trois couches (deux couches cachées et une de sortie) et à trois entrées peut donc se représenter ainsi :

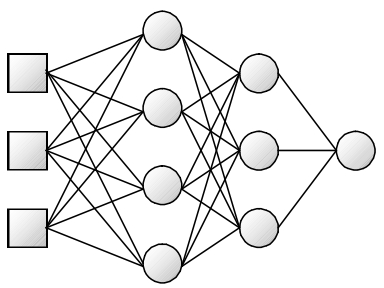
Apprentissage

Les réseaux multicouches utilisent la règle de rétropropagation du gradient décrite plus haut.

Les fonctions de transferts doivent être différentiables. On utilise de ce fait des fonctions sigmoïdes, qui sont des approximations infiniment dérivables de la fonction à seuil de Heaviside.

Applications

Les applications des réseaux non bouclés sont très diverses :

• Reconnaissance de motifs.
• Prévision.
• Apprentissage de comportements ou de jeux.
• etc.

Cas particulier : Les réseaux à fonctions radiales de base

Ces réseaux, appelés réseaux RBF (Radial Basis Functions) sont des réseaux multicouches, à une couche cachée.

Cependant, contrairement aux perceptrons multicouches, les fonctions de transfert de la couche cachée dépendent de la distance entre le vecteur d’entrée et un vecteur centre.

Dans la pratique cette fonction de transfert est souvent le noyau gaussien : $s = \exp{\left(- \left( \frac{||e-c||}{\sigma}\right)^2 \right)}$ où $\sigma$ est le facteur de largeur et $c$ le vecteur centre.

La fonction d’activation de la couche de sortie est une fonction linéaire.

Les trois types de paramètres - centres, largeurs, poids - sont optimisés indépendamment afin d’éviter une lourdeur excessive des calculs.

Conclusion

Les réseaux de neurones présentent donc une très grande diversité.

En effet un type de réseau neuronal est défini par sa topologie, sa structure interne, son algorithme d’apprentissage, et beaucoup de combinaisons sont viables.