WikiMath

---

Catégorie : Seuil

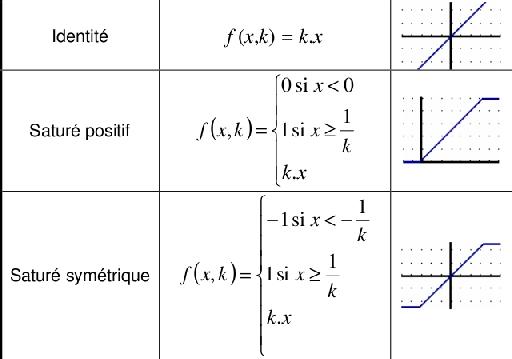
Les fonctions de transfert à seuil

Catégorie : Linéaire

Les fonctions de transfert linéaires

Catégorie : Sigmoïde

Les fonctions de transfert sigmoïdales

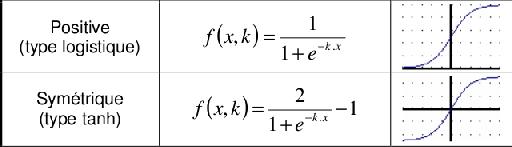
Définition d'une fonction sigmoïdale

Plus généralement, une fonction est dite sigmoïdale si elle est :

• infiniment dérivable, et que sa dérivée admet un et un seul maximum global,
• non linéaire,
• croissante et bornée.

On peut également considérer qu’il s’agit d’une approximation infiniment dérivable de la fonction à seuil de Heaviside.

Précautions d'emploi

Il faut cependant être prudent avec les fonctions sigmoïdes. En effet, pour des entrées grandes, la fonction exponentielle peut provoquer un débordement (overflow).

Il peut être nécessaire de vérifier que l'entrée n'est pas trop grande avant d'appliquer l'équation générale.

Il est bien sûr possible de discrétiser ces fonctions (afin de stocker des entiers).

On peut également appliquer un coefficient additif à la fonction, et simuler un seuil comme vu plus haut avec une entrée supplémentaire fixe au réseau.}

Travaux Pratiques : Développement de la classe FonctionTransfert

1. Construisez la classe FonctionTransfert avec une seule méthode fonction qui renvoie la variable 'x qu'on lui fournit en paramètre
2. Construisez les classes FonctionBinaire, FonctionSigne, ..., FonctionSigmoideSymetrique qui héritent de FonctionTransfert.
   • Chaque classe a éventuellement un paramètre transmis au constructeur.
   • Chaque classe surcharge la méthode fonction de manière adéquate.