WikiMath

---

Différents types d'apprentissage

On peut distinguer deux principaux types d'apprentissages :

Supervisé

On fournit au réseau le couple (entrée, sortie) et on modifie les poids en fonction de l'erreur entre la sortie désirée et la sortie obtenue.

Non supervisé

Le réseau doit détecter des points communs aux exemples présentés, et modifier les poids afin de fournir la même sortie pour des entrées aux caractéristiques proches.

La règle de Hebb

La règle de Hebb est la méthode d'apprentissage la plus ancienne (1949), elle est inspirée de la biologie. Le principe est de renforcer les connexions entre deux neurones lorsque ceux-ci sont actifs simultanément.

Cette règle peut être classée comme apprentissage non supervisé, ou supervisé. En effet, on sait calculer directement les poids correspondant à l'apprentissage d'un certains nombres d'exemples.

La règle du delta

La règle

Son but est de faire évoluer le réseau vers le minimum de sa fonction d'erreur. Sous entendu : erreur commise sur l'ensemble des exemples.

Elle est utilisée dans le modèle de l'ADALINE (ADAptive LINear Element).

L'apprentissage

L'apprentissage est réalisé par itération : les poids sont modifiés après chaque exemple présenté.

On obtient le poids à l'instant $t+1$ par la formule :

       $W(t+1) = W(t) + \eta (T - O).E$

Si :

• W est le poids,
• T est la sortie théorique,
• O est la sortie réelle,
• E est l'entrée,
• $\eta$ est un coefficient d'apprentissage (entre 0 et 1) que l'on peut diminuer au cours de l'apprentissage.

Interprétation

On modifie le poids proportionnellement :

• à l’erreur (différence entre sortie théorique et sortie donnée),
• à l’état d’excitation de l’entrée gérée par le poids.

Ainsi le poids ne sera pas modifié si la sortie est celle voulue, ou si le poids n’a joué aucun rôle dans le résultat.

C'est en fait un cas particulier de l'algorithme de rétropropagation du gradient pour un réseau à une couche.

La rétropropagation du gradient

Présentation

Il a fallu attendre le début des années 1980 pour qu’une règle efficace soit mise au point pour l’apprentissage des réseaux multicouches.

Cette règle est une généralisation de la règle du delta. Elle consiste simplement en une descente de gradient, qui est une méthode d’optimisation universelle.

La méthode

On cherche à minimiser une fonction d’énergie d’erreur, qui représente l'erreur entre la sortie désirée et la sortie obtenue.

Pour cela, on suit les lignes de plus grande pente...

Représentation graphique de la méthode

Une fonction d'erreur rapportée à une dimension peut se représenter ainsi :

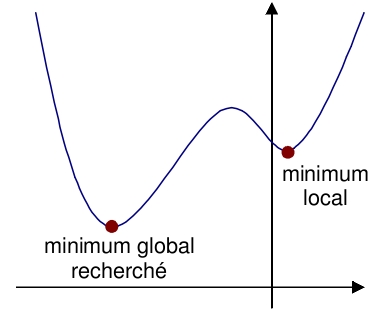
On peut se représenter la descente de gradient comme une bille que l'on poserait sur la courbe, et qui descendrait logiquement la pente.

Le gradient représente la pente selon chaque dimension.

Discussion

L'inconvénient de cette méthode est qu’elle va s’arrêter dans le premier minimum local rencontré.

C'est pourquoi diverses améliorations ont été apportées.

Sujet de TP

1. Mettre en place l'apprentissage dans votre réseau de neurones, en utilisant la règle de Hebb.
2. Faire de même avec la règle du delta.