WikiMath

Inspiré de http://www.coli.uni-saarland.de/~kris/learn-prolog-now (pdf).

Ce TP a pour objectif :

1. de formaliser la notion d'unification en Prolog,
2. d'expliquer la stratégie de recherche employée par Prolog lorsqu'il essaye de déduire de nouveaux faits.

Unification

Présentation

Intuitivement, deux termes peuvent s'unifier :

• s'ils sont égaux;
• s'ils contiennent des variables qui peuvent être instanciées avec des termes, de sorte que les termes résultants soient égaux.

L'unification se note avec un = en Prolog.

  ?- X = mia

  yes

Donnons quelques exemples et contre-exemples, pour bien comprendre de quoi il s'agit.

Exemple de termes unifiables

Commençons par donner des exemples de termes unifiables :

• Les atomes mia et mia, les nombres 42 et 42, les variables X et X, et les termes complexes woman(mia) et woman(mia) car les termes sont à chaque fois identiques.

  ?- X = X.

  ?- mia = mia.

  yes
  ?- 42 = 42.

  yes

  ?- woman(mia) = woman(mia).

  yes

• mia et X, ou alors woman(X) et woman(mia). En effet, ces termes peuvent être rendus égaux en instançiant à chaque fois X par mia :

  ?- mia = X.

  yes
  ?- woman(X) = woman(mia).

  X = mia

  yes

• X et Y : il suffit pour cela de remplacer X et Y par une même constante quelconque :

  ?- X = Y.

  yes

• kill(shoot(gun),Y) et kill(X,stab(knife)) : il suffit pour cela de remplacer X par le terme shoot(gun) et Y par le terme stab(knife) :

  ?- kill(shoot(gun),Y) = kill(X,stab(knife)).

  Y = stab(knife)

  yes

Exemple de termes non unifiables

Des termes sans variable ne peuvent être unifiés :

  ?- woman(mia) = woman(vincent).

  no

De même, les termes suivants ne peuvent pas être unifiés

  ?- loves(vincent,X)=loves(X,mia).

  no

En effet, la variable X ne peut pas être à la fois égale à mia et à vincent.

Dans le même esprit,

  ?- loves(X,X) = loves(marcellus,mia)

  no

En effet, la variable X ne peut pas être à la fois égale à marcellus et à mia.

Cas de l'unification dans une clause

L'unification réussit dans une clause, si elle se fait avec succès dans tous les buts simultanément. Ainsi,

  ?- X = mia, X = vincent.

  no

a pour réponse non, car la variable X devrait s'unifier simultanément avec mia et vincent.

Programmer à l'aide de l'unification

L'objectif est d'exploiter l'unification pour réaliser des programmes.

On donne une première illustration de comment cela est possible, à l'aide d'un exemple dû à Ivan Bratko (à placer dans un fichier .pl).

  vertical(line(point(X,Y),point(X,Z))).
  horizontal(line(point(X,Y),point(Z,Y))).

Dans ce qui précède,

• point définit un point dont l'abscisse et l'ordonnée sont les deux arguments (dans cet ordre),
• line permet de définir une ligne entre deux points passés en argument.
• vertical et horizontal sont les propriétés de la ligne passée en argument.

Le premier fait est vrai si et seulement si les points passés en paramètre ont même abscisse. Le second fait est vrai si et seulement si les points passés en paramètre ont même ordonnée.

Utilisons cette base de connaissance. Dans une session Prolog, une fois la base de connaissances consultée, testez ce qui suit :

  | ?- vertical(line(point(1,1),point(1,3))).

  yes

La ligne reliant les points (1,1) et (1,3) est effectivement verticale. Poursuivons...

  | ?- vertical(line(point(1,1),point(3,2))).

  no

Même remarque que ci-dessus, pour l'horizontalité de la ligne. Plus fort, maintenant, en utilisant une variable Y :

  | ?- horizontal(line(point(1,1),point(2,Y))).

  Y = 1

  yes

Il y a eu unification. Enfin,

  ?- horizontal(line(point(2,3),P)).

  P = point(_,3) ;

  yes

Ainsi la ligne est horizontale pour tout point P d'abscisse quelconque, et d'ordonnée 3.

Travaux Pratiques

Exercice

Lesquelles de ces paires de termes s'unifient ? Le cas échéant, donnez les instanciations de variables qui permettent l'unification.

   1. bread = bread
   2. ’Bread’ = bread
   3. ’bread’ = bread
   4. Bread = bread
   5. bread = sausage
   6. food(bread) = bread
   7. food(bread) = X
   8. food(X) = food(bread)
   9. food(bread,X) = food(Y,sausage)
  10. food(bread,X,beer) = food(Y,sausage,X)
  11. food(bread,X,beer) = food(Y,kahuna_burger)
  12. food(X) = X
  13. meal(food(bread),drink(beer)) = meal(X,Y)
  14. meal(food(bread),X) = meal(X,drink(beer))

Exercice

Soit la base de connaissances suivante

  house_elf(dobby).
  witch(hermione).
  witch(’McGonagall’).
  witch(rita_skeeter).
  magic(X):-house_elf(X).
  magic(X):-wizard(X).
  magic(X):-witch(X).

1. Parmi les requêtes ci-dessous, lesquelles peuvent être satisfaites ?
2. Le cas échéant, donnez les instanciations de variables qui permettent l'unification.
3. Vérifier le résultat avec Prolog.

   1. ?- magic(house_elf).
   2. ?- wizard(harry).
   3. ?- magic(wizard).
   4. ?- magic(’McGonagall’).
   5. ?- magic(Hermione).

Stratégie de recherche

Supposons la base de connaissances suivante :

  f(a).
  f(b).
  g(a).
  g(b).
  h(b).
  k(X) :- f(X),g(X),h(X).

Si on soumet la requête

  | ?- k(X).

Prolog répond

  yes

  X = b.

Comment aboutit-il à ce résultat ? Comme suit.

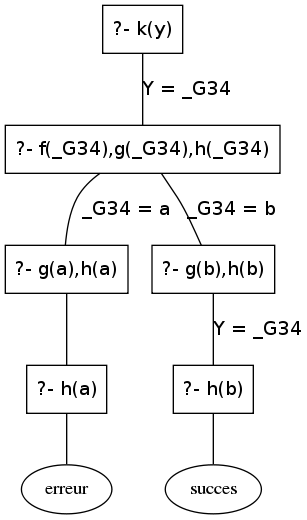
Prolog construit à la volée l'arbre de recherche ci-dessus. Voyons comment.

• Prolog ne peut unifier k(X) qu'avec la règle k(X) :- f(X),g(X),h(X). Pour cela il génère une variable _G348 qui est liée à Y.
• Il cherche ensuite un individu qui vérifie f, g, et h : il satisfera alors k. Prolog construit le second nœud k(_G348) :- f(_G348),g(_G348),h(_G348).
• Prolog cherche ensuite à satisfaire f(_G348). Pour cela il utilise le fait f(a). En unifiant f(_G348) à f(a), X est instancié à a.
• Il reste à résoudre le but g(a),h(a). Le fait g(a) étant dans la base, il ne lui reste plus qu'à résoudre h(a). Cependant, il n' a pas les moyens de déduire ce but. Il échoue donc.
• Finalement, Prolog «backtrack» jusqu'au dernier choix effectué, c'est-à-dire au moment où il a instancié _G348 avec a. Il unifie alors f(_G348) avec f(b), donc il instancie X avec b.

Travaux pratiques

Exercice

Soit la base de connaissances suivante

  loves(vincent,mia).
  loves(marcellus,mia).
  jealous(X,Y) :- loves(X,Z),loves(Y,Z).

Si on soumet la requête

  jealous(X,Y)

que va répondre Prolog ? Le vérifier.

Exercice

Considérons le lexique d'une mini-grammaire suivant :

  word(article,a).
  word(article,every).
  word(noun,criminal).
  word(noun,’big kahuna burger’).
  word(verb,eats).
  word(verb,likes).
  sentence(Word1,Word2,Word3,Word4,Word5) :-
           word(article,Word1),
           word(noun,Word2),
           word(verb,Word3),
           word(article,Word4),
           word(noun,Word5).

On vous demande de...

1. Décrire le prédicat word.
2. Décrire le prédicat sentence.
3. Quelle requête doit on poser pour trouver toutes les phrases que cette grammaire peut engendrer.
4. Énoncer ces phrases dans l'ordre où Prolog va les engendrer et vérifier en implantant.