WikiMath

Inspiré de http://www.coli.uni-saarland.de/~kris/learn-prolog-now (pdf).

Ce TP a pour objectif :

• de présenter les définitions récursives en Prolog,
• de mesurer l'impact de l'ordre des règles et des buts de celles-ci, sur l'arbre de recherche engendré.

Définitions récursives

Exemple d'introduction

Soit la base de connaissances suivante :

  is_digesting(X,Y) :- just_ate(X,Y).
  is_digesting(X,Y) :-
                 just_ate(X,Z),
                 is_digesting(Z,Y).

  just_ate(mosquito,blood(john)).
  just_ate(frog,mosquito).
  just_ate(stork,frog).

Les règles de cette base de connaissance ont la sémantique suivante :

• La première clause signifie que «si X vient de manger Y, alors X est en train de digérer Y».
• La seconde clause signifie que «si X vient de manger Z et que Z est en train de digérer Y, alors X est en train de digérer Y».

La définition du prédicat is_digesting (est entrain de digérer) est récursive. En effet, is_digesting apparaît en même temps dans la tête et dans le corps de la seconde règle. La sortie de la récursivité se fait grâce à la première règle de la base de connaissance.

Pour déterminer si X digère Y, Prolog dispose d'une seconde stratégie : chercher un Z qui vient d'être mangé par X et essayer de déduire si Z digère Y, comme représenté sur la figure suivante.

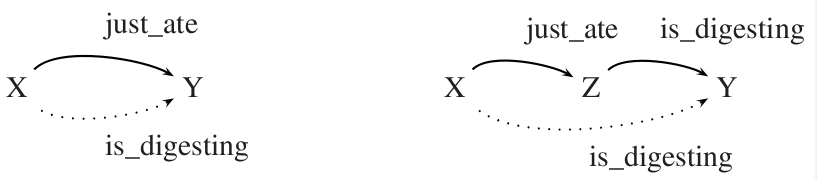
Face à la requête

  ?- is_digesting(stork,mosquito).

Prolog construit l'arbre de recherche comme suit :

• Il essaye d'exploiter la première règle. Après unification, il cherche à déduire just_ate(stork,mosquito). Aucun des fais ni aucune des règles ne permet de l'établir.
• Il essaye d'exploiter la seconde règle. Après unification, il cherche à déduire simultanément just_ate(stork,_G35) et is_digesting(_G35,mosquito).
  • Le but just_ate(stork,_G35) est obtenu en unifiant _G35 à frog, grâce au fait just_ate(stork,frog)
  • Le but is_digesting(frog,mosquito) est obtenu directement car est un fait de la base de connaissances.

Conditions d'arrêt

Attention, il est impératif de définir la clause permettant la sortie de la récursivité.

Par, exemple si on considère la règle

  p :- p.

et la requête suivante :

  ?- p.

pour établir p, Prolog essaie d'établir p à l'aide de la règle, et boucle indéfiniment.

Travaux pratiques

Soit la base de connaissance suivante

  child(martha,charlotte).
  child(charlotte,caroline).
  child(caroline,laura).
  child(laura,rose).

qui signifie que Martha est un enfant de Charlotte, Charlotte un enfant de Caroline ...

1. A l'aide du prédicat child, définir de manière récursive le prédicat descend(X,Y) qui précise que X est un descendant de Y.
2. Construire l'arbre de déduction qui permet à Prolog de déduire que Martha est une descendante de Laura.

Ordonnancement des règles et ordonnancement des buts

De l'importance d'être ordonné

On rappelle que, pour effectuer des déductions, Prolog...

• parcourt les clauses du haut vers le bas,
• parcourt les buts de la gauche vers la droite à l'intérieur des clauses,
• utilise le backtrack pour revenir sur ses mauvais choix.

Ordonner différemment les clauses peut avoir des conséquences importantes concernant l'arbre de déduction, les deux exemples suivants en donnent une illustration.

Exemple d'inversion de deux clauses Prolog

On considère la base de faits :

  child(martha,charlotte).
  child(charlotte,caroline).
  child(caroline,laura).
  child(laura,rose).

Dans le premier cas, on ajoute la définition récursive de descend suivante :

  descend(X,Y) :- child(X,Y).
  descend(X,Y) :- child(X,Z),descend(Z,Y).

Si on lance la requête

  ?-descend(martha,D).

on obtient l'arbre de déduction suivant

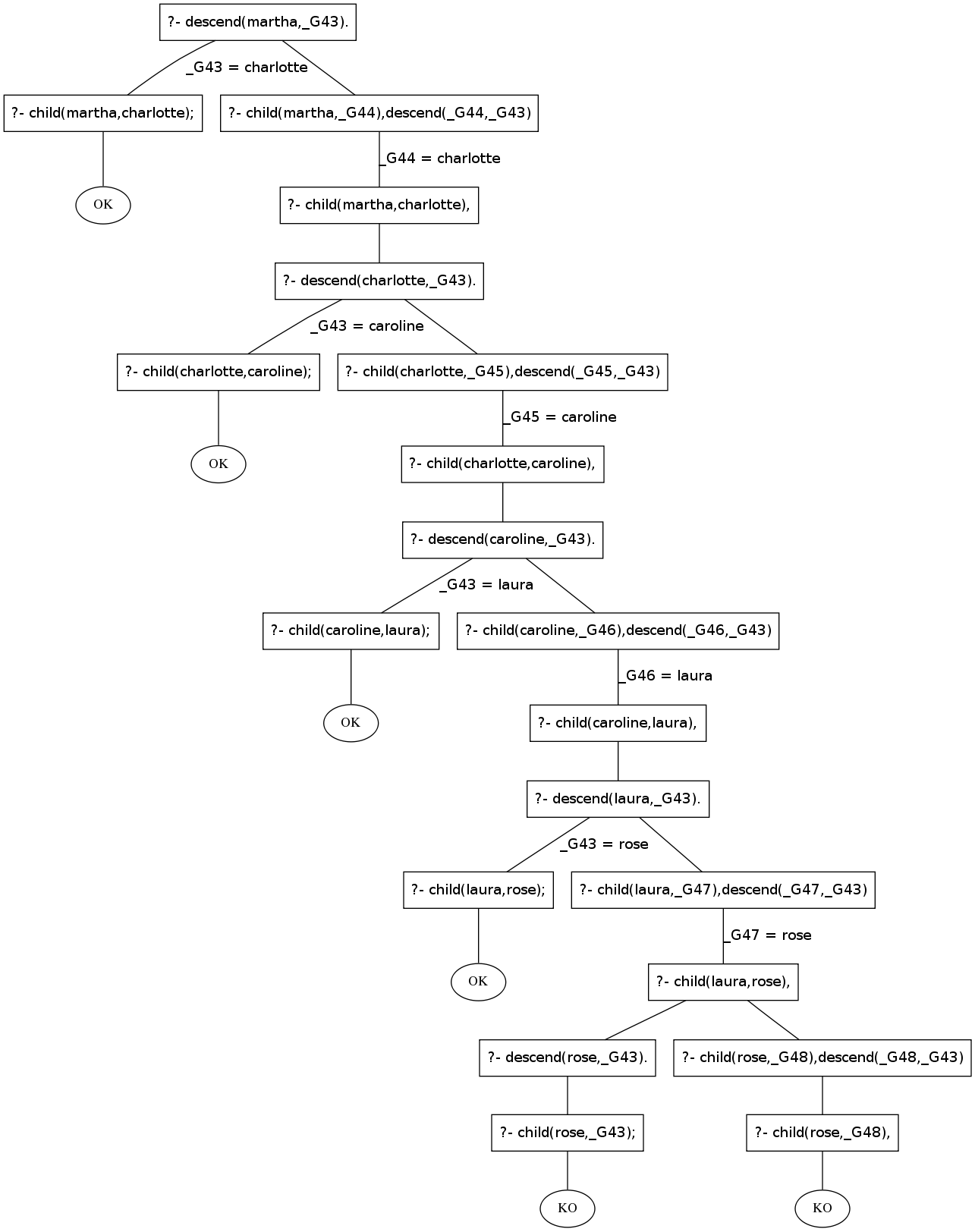
et donc les réponses

  D = charlotte ;
  D = caroline ;
  D = laura ;
  D = rose ;
  fail.

Dans le second cas, on inverse les deux clauses pour avoir à la place :

  descend(X,Y) :- child(X,Z),descend(Z,Y).
  descend(X,Y) :- child(X,Y).

Si on lance la requête

  ?-descend(martha,D) 

on a l'arbre de déduction suivant :

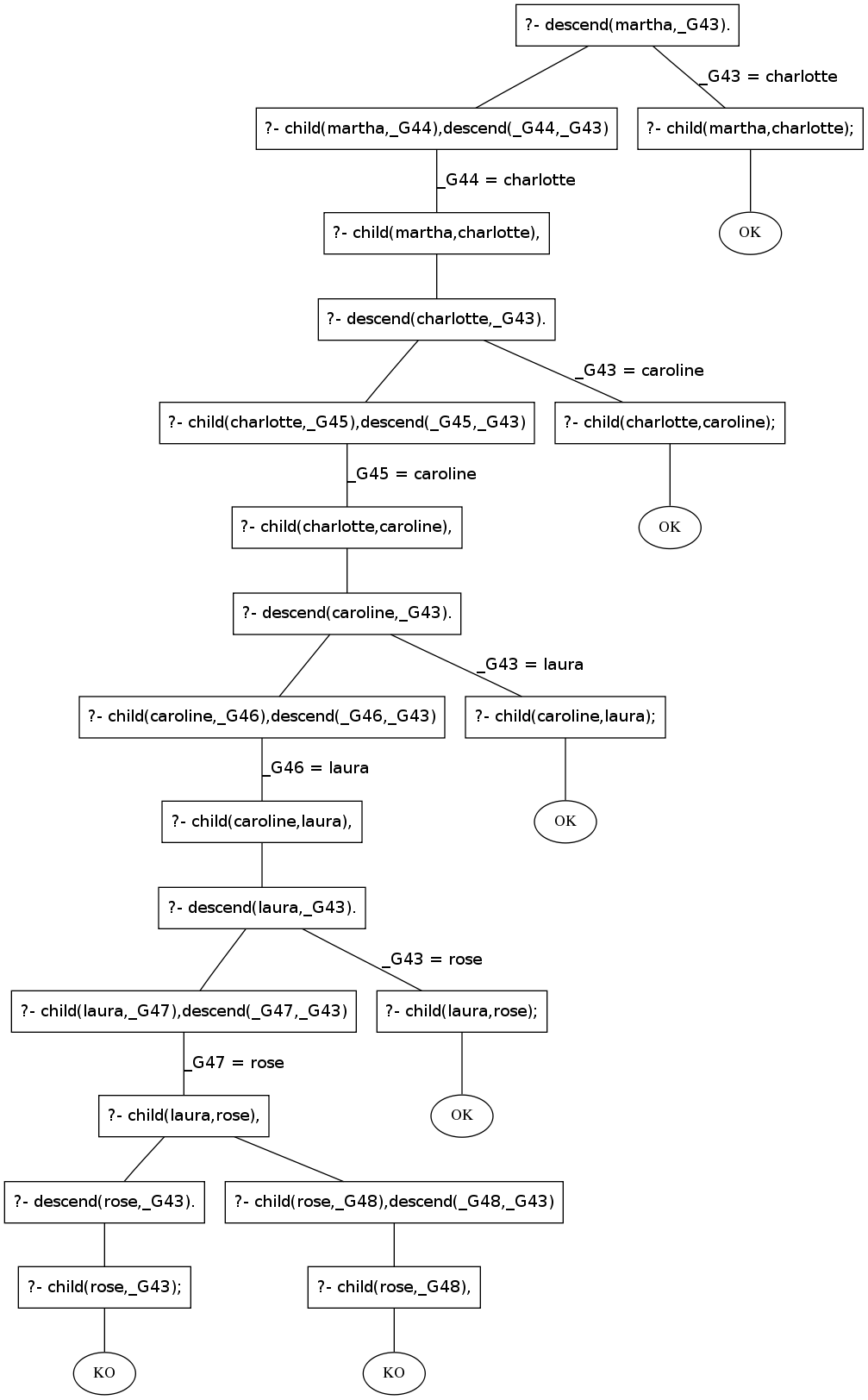
et donc les réponses suivantes :

  D = rose ;
  D = laura ;
  D = caroline ;
  D = charlotte;
  fail.

Exemple d'inversion de deux buts Prolog

Si on pose maintenant

  descend(X,Y) :- descend(Z,Y),child(X,Z),
  descend(X,Y) :- child(X,Y).

qui a le même sens logique, on a l'arbre suivant (qui est infini)

Pour conclure, on adoptera les règles suivantes :

• on place en premier la(les) clause(s) permettant de sortir de la récursivité;
• dans une clause avec récursivité, les buts induisant la récursivité doivent être placé le plus vers la droite possible.

Travaux pratiques

Matriochkas

On considère les poupées russes (matriochkas) suivantes:

1. Écrire la base de faits correspondant à l'inclusion immédiate d'une poupée dans une autre.
2. Définir récursivement le prédicat intérieur(X,Y) qui est vrai si la poupée X est incluse dans Y (par exemple, Irina est à l'intérieur d'Olga).
3. Utiliser cette base de connaissance, pour vérifier vos résultats.

Correction : ici.

Réseau ferré

La base de faits suivante explicite les villes qu'il est possible de relier via un train direct.

  trainDirect(forbach,saarbruecken).
  trainDirect(freyming,forbach).
  trainDirect(fahlquemont,stAvold).
  trainDirect(stAvold,forbach).
  trainDirect(saarbruecken,dudweiler).
  trainDirect(metz,fahlquemont).
  trainDirect(nancy,metz).

Construire un prédicat récursif allerDe(X,Y), qui est vrai si l'on peut allez de X à Y.

Correction : ici.