---

Objectifs

Nous allons voir ici un petit programme, pas si évident, dans lequel les connaissances précédentes vont être mises en oeuvre.

Le but est le suivant :

• On souhaite placer un cube, surmonté d'une sphère à l'origine du repère.
• On veut aussi que les flèches haut et bas servent à avancer ou reculer, dans la direction du centre de l'écran.
• On veut encore que les flèches droite et gauche réalisent un décalage dans la direction adéquate.
• Que bouger la souris ait le même effet que bouger la tête dans la vie de tous les jours.

Selon ce que vous voulez en faire, cette gestion de la vision et du déplacement peut ne pas convenir : tel quel, si on regarde en haut, et qu'ensuite on « avance », cette « avancée » se traduit dans les faits par une montée, une prise d'altitude : on avance vers le haut.

Ce programme scene.py est donc à adapter en fonction des besoins.

Réalisation

Préliminaires

Conventions

On note M(Xm,Ym,Zm) le centre de la caméra, et O(Xo,Yo,Zo) le point que l'on vise :

  gluLookAt(Xm,Ym,Zm,Xo,Yo,Zo,0,1,0)

A l'origine,

  Xm=-3,Ym=0,Zm=0,
  Xo=0,Yo=0,Zo=0.

et on fait en sorte que OM=3, quelles que soient les transformations appliquées à O et M : le point visé sera toujours à trois unités du centre de la caméra.

Début du main()

On retrouve donc ce qui suit dans main() :

    global X, Y, Xm, Ym, Zm, Xo, Yo, Zo, A1, A2

    X, Y = 980, 660
    Xm, Ym, Zm =-3, 0, 0
    Xo, Yo, Zo = 0, 0, 0
    A1, A2 = 0., 0.

On peut changer cela en modifiant les premières positions de ces points. Ainsi, Xm=-6 dans l'initialisation de M a pour effet de constamment maintenir une distance de 6 unités entre O et M (point visé plus distant.)

Récapitulation

Un schéma pour récapituler la scène initiale :

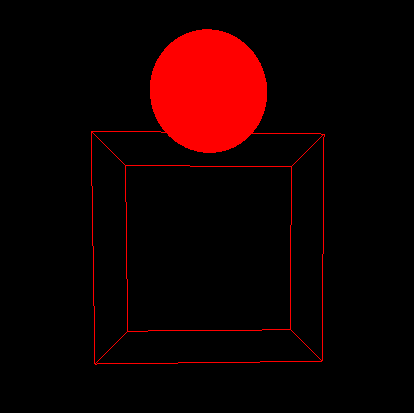
O se confond alors avec le centre de l'espace $\Omega$.

L'avancement au clavier

Flèches haut et bas

On veut « avancer » dans la direction $\overrightarrow{MO}$ dès que la touche flèche-haut est pressée :

• Les nouveaux points O et M sont donc égaux aux anciens, augmentés d'une fraction du vecteur $\overrightarrow{OM}$.
• On souhaite un « petit » déplacement à chaque pression de la touche, par exemple de 0,1 unités.

Comme OM=3, on en déduit que la fraction ci-dessus vaut $\frac{0,1}{OM}$ (en fait $\frac{0,1}{3}$, mais on préfère laisser OM, au cas où on souhaiterais augmenter cette distance.)

Ainsi, le nouveau O, c'est l'ancien O plus $\frac{0,1}{OM} \overrightarrow{OM}$. Or

$\overrightarrow{OM} = ( Xo-Xm, Yo-Ym, Zo-Zm)$

donc les nouvelles coordonnées de O seront

$Xo = Xo - 0.1 \frac{Xo-Xm}{OM}, Yo = Yo - 0.1 \frac{Yo-Ym}{OM}, Zo = Zo - 0.1 \frac{Zo-Zm}{OM}$

et on fait pareil pour M, ce qui donne ce bout de programme suivant :

    global Xm, Ym, Zm, Xo, Yo, Zo, A1, A2

    if (argv[0]==GLUT_KEY_UP):
        OM=sqrt((Xo-Xm)*(Xo-Xm)+(Yo-Ym)*(Yo-Ym)+(Zo-Zm)*(Zo-Zm))

        Xm=Xm+0.1*(Xo-Xm)/OM
        Ym=Ym+0.1*(Yo-Ym)/OM
        Zm=Zm+0.1*(Zo-Zm)/OM

        Xo=Xo+0.1*(Xo-Xm)/OM
        Yo=Yo+0.1*(Yo-Ym)/OM
        Zo=Zo+0.1*(Zo-Zm)/OM


    if (argv[0]==GLUT_KEY_DOWN):
        OM=sqrt((Xo-Xm)*(Xo-Xm)+(Yo-Ym)*(Yo-Ym)+(Zo-Zm)*(Zo-Zm))

        Xm=Xm-0.1*(Xo-Xm)/OM
        Ym=Ym-0.1*(Yo-Ym)/OM
        Zm=Zm-0.1*(Zo-Zm)/OM

        Xo=Xo-0.1*(Xo-Xm)/OM
        Yo=Yo-0.1*(Yo-Ym)/OM
        Zo=Zo-0.1*(Zo-Zm)/OM

    glutPostRedisplay()

On le placera dansglutSpecialFunc(), car les flèches font parties, on le rappelle, des touches dites spéciales).

Droite et gauche

Pour les touches gauche et droite, c'est presque pareil : on souhaite, cette fois-ci, se déplacer suivant une direction orthogonale au plan $X\Omega Z$, c'est-à-dire suivant le vecteur (Zo-Zm,Yo-Ym,-Xo+Xm) :

On insère donc le bout de code suivant dans la fonction clavierSpecial() ci-dessus :

    if (argv[0]==GLUT_KEY_RIGHT):

        OM=sqrt((Xo-Xm)*(Xo-Xm)+(Yo-Ym)*(Yo-Ym)+(Zo-Zm)*(Zo-Zm))

        Xm=Xm-0.1*(Zo-Zm)/OM
        Ym=Ym-0.1*(Yo-Ym)/OM
        Zm=Zm-0.1*(-Xo+Xm)/OM

        Xo=Xo-0.1*(Zo-Zm)/OM
        Yo=Yo-0.1*(Yo-Ym)/OM
        Zo=Zo-0.1*(-Xo+Xm)/OM


    if (argv[0]==GLUT_KEY_LEFT):
        OM=sqrt((Xo-Xm)*(Xo-Xm)+(Yo-Ym)*(Yo-Ym)+(Zo-Zm)*(Zo-Zm))

        Xm=Xm+0.1*(Zo-Zm)/OM
        Ym=Ym+0.1*(Yo-Ym)/OM
        Zm=Zm+0.1*(-Xo+Xm)/OM

        Xo=Xo+0.1*(Zo-Zm)/OM
        Yo=Yo+0.1*(Yo-Ym)/OM
        Zo=Zo+0.1*(-Xo+Xm)/OM

Le déplacement à la souris

Préliminaires

On doit maintenant s'occuper de la modification de la vue lors du déplacement de la souris.

C'est le point O qui change avec le mouvement de la souris...ce qui entraîne la modification du vecteur de déplacement $\overrightarrow{MO}$ : rappelons que si l'on regarde par exemple vers le bas, puis si l'on avance, alors on se déplacera vers le bas. (D'autres comportements sont possibles. Ce qui importe, c'est de comprendre la méthode.)

On veut que le point O change lorsque l'on bouge la souris, sans qu'il y ait de clic. On va donc faire appel, dans le main(), à la fonction glutPassiveMotionFunc(souris), où la fonction souris() sera chargée de modifier Xo, Yo, Zo lors du déplacement de la souris.

De la position de la souris... à l'angle associé

Notre fenêtre fait 980 x 660 pixels :

    X=980
    Y=660

Lorsque la souris touche le bord haut de la fenêtre, on aimerait regarder au-dessus de nous, à la verticale : notre regard ferait alors un angle de$\frac{\pi}{2}$ avec l'horizon.

Lorsque la souris touche le bord bas de la fenêtre, on regarde nos pieds, notre regard faisant un angle de $-\frac{\pi}{2}$ avec l'horizon.

De même, en positionnant notre souris sur le bord droit de la fenêtre, on aimerait que notre tête tourne de 90° vers la droite. Idem pour le bord gauche.

Notre première tâche, dans la fonction mouse(), est donc de transformer la position de la souris en angles que formeraient notre regard entre l'horizon d'une part, et la verticale du lieu :

    def souris(*argv):
        global X, Y, Xm, Ym, Zm, Xo, Yo, Zo, A1, A2

        A2=(float(argv[0])-float(X)/2)/(float(X)*3.141592)
        A1=(float(Y)/2-float(argv[1]))/(float(Y)*3.141592)

        glutPostRedisplay()

Dans ce qui précède, on transforme l'écart entre la position (argv[0],argv[1]) de la souris et le centre (X/2,Y/2) de l'écran, en angles A1 et A2, tels que $A2=\frac{\pi}{2}$, quand la souris est à droite de l'écran (quand on regarde à droite), et $A1=\frac{\pi}{2}$, quand la souris est en haut de l'écran (quand on regarde au-dessus de notre tête) :

figu3.jpg

Bouger la souris revient donc à changer les angles A1 et A2 que fait le point O dans le repère (M;X,Y,Z) : on doit donc effectuer une rotation d'angle A2 autour de MY, puis une rotation d'angle A1 autour de MZ.

Seulement, il faut faire attention au détail suivant : quand la souris bouge un peu, les angles font de même (par exemple, A1 passe de 47,3° à 47,6°)...la rotation autour de MZ doit donc être d'un angle égal à cette différence (0,3° dans notre exemple.)

Dans notre programme, on a commencé par faire des rotations d'angles -A1 et -A2, pour ensuite relever les nouveaux angles (ceux après déplacement de la souris), et faire enfin les rotations d'angles A1 et A2 (qui ont été modifiés) :

• on envoie O sur l'axe MX par des rotations d'angles -A1 et -A2

        Xo=Xm+(Xo-Xm)*cos(-A2)-(Zo-Zm)*sin(-A2)
        Zo=Zm+(Xo-Xm)*sin(-A2)+(Zo-Zm)*cos(-A2)
        Xo=Xm+(Xo-Xm)*cos(-A1)-(Yo-Ym)*sin(-A1)
        Yo=Ym+(Xo-Xm)*sin(-A1)+(Yo-Ym)*cos(-A1)

• on donne les nouvelles valeurs aux angles

        A2=(float(argv[0])-float(X)/2)/(float(X)*3.141592)
        A1=(float(Y)/2-float(argv[1]))/(float(Y)*3.141592)

• on fait enfin subir à O une rotation d'axe MY, angle A2, puis d'axe MX, angle A1 :

        Xo=Xm+(Xo-Xm)*cos(A2)-(Zo-Zm)*sin(A2)
        Zo=Zm+(Xo-Xm)*sin(A2)+(Zo-Zm)*cos(A2)
        Xo=Xm+(Xo-Xm)*cos(A1)-(Yo-Ym)*sin(A1)
        Yo=Ym+(Xo-Xm)*sin(A1)+(Yo-Ym)*cos(A1)

        glutPostRedisplay()

Il se passe finalement ce que l'on souhaitait, comme vous pouvez vous en assurer vous-même.

Terminons ce tp en remarquant l'allure des rotations : si elles semblent si compliquées, c'est parce qu'elles se font autour de M, elles ne sont pas centrées à l'origine. Il a donc fallu faire une translation de vecteur, suivie de la rotation à proprement parlé, et terminée par la translation inverse, de vecteur .

Conclusion

Cette brève introduction à la bibliothèque OpenGL, puissante et compliquée, est terminée. Vous connaissez dorénavant le strict minimum pour réaliser une scène 3d et permettre à l'utilisateur de s'y déplacer. A vous d'approfondir le sujet, si cela vous tente...