WikiMath

Les paramètres de la caméra

Nous allons maintenant changer le point de vue de la scène.

Imaginons pour cela que nous enregistrions la scène 3d au moyen d'une caméra. Il y a trois paramètres à régler, à savoir :

• où placer la caméra (son centre C),
• vers quel point l'orienter (le point O),
• enfin, placer la caméra horizontalement, ou la tourner suivant l'axe CO ?

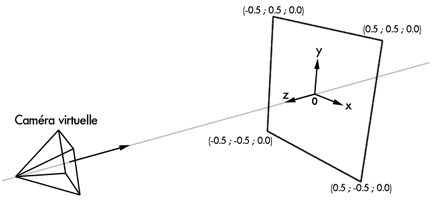
Ces trois valeurs se changent à l'aide de la fonction gluLookAt(), qui admet neuf paramètres :

• les trois premiers correspondent aux coordonnées de C,
• les trois suivants à celles de O,
• et les trois dernières au vecteur d'inclinaison de la caméra.

Notez les valeurs par défaut de ces paramètres :

• C est à l'origine du repère,
• O est sur le demi-axe des z négatifs,
• et le vecteur d'inclinaison est (0,1,0).

Définition du champ de vision

Mais avant de positionner notre caméra dans la scène, il faut la régler (ou plus exactement définir notre champ de vision : notre oeil, par exemple, ne distingue pas les objets trop proches ou trop éloignés, ni sur les côtés), avec la fonction gluPerspective(), c'est-à-dire :

1. Donner l'angle d'ouverture de la camera,
2. Donner la distance minimale, en-deça de laquelle les objets n'apparaissent pas à l'écran, (étant trop proches de l'objectif),
3. Donner la distance maximale, au-delà de laquelle les objets sont trop loin pour être apparents,
4. Enfin, préciser si l'on souhaite que les longueurs des objets soient rapportées à la dimension de la fenêtre, ou non (dans le premier cas, un carré dans une fenêtre rectangulaire apparaîtra sous la forme d'un rectangle).

La figure ci-dessous illustre cela :

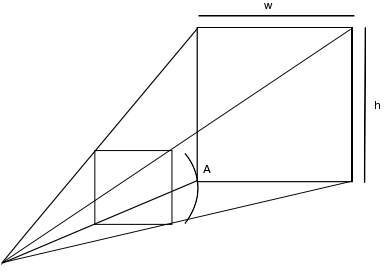
La partie capturée par la caméra se trouve dans la partie basse de cette pyramide renversée.

L'angle A au sommet de la pyramide correspond ici à l'angle d'ouverture de la caméra (dans le plan yOz).

Il ne reste plus qu'à connaître le rapport w/h pour avoir le volume exact de la scène à représenter à l'écran. En effet, à une largeur de pyramide correspondra une unique longueur, donc en augmentant notre largeur de fenêtre, la longueur de la scène à afficher changera aussi.

Ainsi, par exemple,

gluPerspective(45.0,float(w)/h,1.,10.)

définit une caméra avec un angle d'ouverture de 45°, une base de pyramide ayant un rapport de largeur sur longueur égal à w/h, et tous les points trop proches (z<1.0 par-rapport au z de la caméra) ou trop loin (z>10.0) ne seront pas affichés.

Remarquons enfin qu'une autre fonction,

glFrustum(gauche,droite,bas,haut,proche,éloigné),

fait le même travail, sauf qu'on spécifie les 4 coordonnées définissant le premier rectangle de la figure précédente, les deux dernières variables étant les mêmes que pour gluPerspective().

Emplacement de gluPerspective()

Reste à savoir où placer gluPerspective().

Il faut d'abord signaler dans le main() qu'une fonction, que l'on nomme traditionnellement reshape(), est chargée de gérer l'affichage de la scène (contenue dans la fonction ecran()).

C'est-à-dire que la fonction reshape() est sensée :

• Gérer ce que la caméra peut voir en pointant dans une direction donnée.
• Gérer quel type de projection utiliser pour représenter la scène 3D à l'écran (qui est un plan) : projection droite ou perspective.
• S'occuper enfin de paramétrer la caméra, comme détaillé dans le point précédent.

Cela se fait, comme d'habitude, au moyen d'un glutReshapeFunc(reshape).

La partie de programme qui suit illustre ce principe :

    glViewport(0,0,args[0],args[1])
    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    gluPerspective(60.0,float(args[0])/args[1],1.,10.)

    glutInit(sys.argv)
    glutInitDisplayMode(GLUT_RGBA)
    glutInitWindowPosition(100,100)
    glutInitWindowSize(320,320)
    glutCreateWindow("Une table")
    glutDisplayFunc(ecran)
    glutReshapeFunc(reshape)
    glutMainLoop()

(Il manque ici le détail de la fonction ecran(), donnant du sens à ce programme.)

Les paramètres passés à la fonction reshape() via OpenGL sont :

• la largeur w de la fenètre (en pixels)
• sa hauteur h actuelle

On parle ici de la fenêtre qui vient d'être créée, ou déplacée, ou redimensionnée.

Ces paramètres se retrouvent naturellement dans la fonction gluPerspective() pour obtenir exactement le champ de vision détaillé au point précédent.

glLoadIdentity()

Expliquons maintenant le glLoadIdentity().

Comme dans le cours d'algèbre-géométrie, l'espace est un ensemble de points, et de volumes pleinement définis par la donnée de points caractéristiques : les sommets d'un cube, etc.

Et, comme dans notre cours, effectuer un déplacement revient à multiplier ces points à l'aide de matrices de transformation : homothétie, rotation, projection, etc. La matrice produit résultante s'appelle alors la « matrice active. »

Donc, pour obtenir une représentation plane (dans notre écran) à partir d'un espace de points 3d (notre scène), OpenGL multiplie, à notre demande, chaque point de l'espace par les matrices de transformation adéquates.

Quand on demande plusieurs opérations de ce type, OpenGL multiplie les matrices correspondantes entre-elles, et attend le signal pour appliquer la matrice résultante (c'est-à-dire la « matrice active ») à l'ensemble des points.

On peut ainsi enchaîner les opérations géométriques à effectuer en rajoutant des matrices au produit en mémoire. Cependant, il faut enlever ce produit matriciel de la mémoire, réinitialiser la « matrice active » à chaque fois que l'on souhaite faire une nouvelle opération, sans quoi OpenGL rajoutera sans cesse les nouvelles opérations aux anciennes, donnant un produit matriciel sans fin.

C'est le sens de glLoadIdentity(), qui transforme la « matrice active », la rendant égale à la matrice identité.

Les trois types d'opérations matricielles

En fait, OpenGL distingue trois types d'opérations matricielles, concernant respectivement :

• La modélisation-visualisation, qui a trait
  • à la visualisation : positionnement de la caméra, via gluLookAt(),
  • à la modélisation : au positionnement et à l'orientation du modèle, à son éventuel agrandissement, bref à toutes les opérations de translations, rotation et homothétie applicables aux points définissant l'objet, via glTranslatef(), glRotatef(), et glScalef().

• La projection, et qui correspond en gros au choix de l'objectif de la caméra : déterminer le champ de vision (via gluPerspective(), ou glFrustum()). C'est ce qui a été abordé dans la précédente section.

• Le placage de textures.

Pour simplifier la tâche du programmeur, la « matrice active » est donc le produit de trois matrices, correspondant respectivement à chacun des points précédents. Ainsi, par exemple, on peut vouloir changer la projection sans toucher à notre modèle, ni à ses textures.

Comment préciser la matrice à modifier

Il convient donc, avant d'utiliser glLoadIdentity(), de préciser quelle partie de la matrice active on souhaite initialiser. Pour cela, on spécifie avec la fonction glMatrixMode() quelle est la partie concernée de la matrice active :

• glMatrixMode(GL_PROJECTION) signifie que toutes les opérations concernées se font sur la partie projection de la matrice active,
• glMatrixMode(GL_MODELVIEW) signifie que la partie modifiable de la matrice active est alors celle concernant la modélisation-visualisation,
• glMatrixMode(GL_TEXTURE) fait pareil, sur la partie textures de la matrice active.

Il faut donc, à chaque fois, préciser sur quelle partie porte nos lignes de code (visualisation-modélisation, cadrage-projection, ou textures). Notez cependant que, par défaut, OpenGL est en glMatrixMode(GL_MODELVIEW).