WikiMath

Réduction d'une image

• Réduire une image revient à réduire la résolution de l'image
  • n fois moins de pixels en hauteur et en largeur => résolution n fois plus grossière;
  • 1 pixel de l'image réduite correspond à un bloc de n x n pixels dans l'image
  à résolution fine.
• Méthode de réduction la plus commune
  1. Découpage de l'image originelle en blocs de n x n pixels;
  2. calcul sur chaque bloc de la moyenne des intensités;
  3. l'intensité moyenne d'un bloc est l'intensité du pixel correspondant au bloc
  dans l'image réduite.
• Illustration de la réduction (512² en 256² - 128² - 64²)

Agrandissement d'une image

• Agrandir une image revient à augmenter la taille des pixels
  • n fois plus de pixels en hauteur et en largeur => pixels n fois plus grands
  => résolution n fois plus grossière.
• Méthode d'agrandissement la plus commune
  • Chaque pixel de l'image originelle est remplacé par un bloc de n x n pixels
  de même intensité.
  • Procédé d'interpolation au plus proche voisin.
• Effet de crénelage des contours obliques et de brouillage
  • Augmente avec le facteur d'agrandissement.
  • Pixelisation rendant méconnaissables beaucoup de détails.
• Atténuation
  • Par application dans chaque bloc d'une :
    • interpolation bilinéaire;
    Variation linéaire des intensités dans chaque direction.
    • interpolation par splines
    Transition liss de niveaux de gris entre carrés voisins
  • Par l'utilisation de techniques de lissage spécifiques.

Rééchantillonnage d'une image

• Rééchantillonner c'est modifier le nombre de pixels
  • Sous-échantillonnage => réduction
    • suppression de pixels
  • Sur-échantillonnage => augmentation
    • ajout de pixels par interpolation
• Le redimensionnement d'une image consiste donc en un rééchantillonnage

• Un rééchantillonnage peut détériorer la qualité et la netteté
  • Importance du choix de la méthode d'interpolation
    • plus proche voisin : rapide, mais la moins précise;
    • bilinéaire : qualité moyenne (calcul sur 4 pixels);
    • bicubique : lente, mais la plus précise (analyse de 16 pixels).

Transformation rigide

Qu'est-ce qu'une transformation rigide

• Combinaison d'une rotation et d'une translation.
• Transformation définie par un vecteur de paramètres $\Theta$

$\Theta=\left(t_x,t_y,\theta_z\right)^T$,

• Repère orthonormé direct

Formulation de la transformation - rotation discrète

• Soient
  • $S=\left(x,y\right)^T$ un pixel de l'image de départ;
  • $S'=\left(x',y'\right)^T$ son image par la transformation dans l'image d'arrivée

$S'=T_{\Theta}(S)$.

• Formulation

$\left(\begin{array}{c} x' \\ y' \end{array}\right) = \left[\left(\begin{array}{cc} \cos \theta_z & \sin \theta_z \\ -\sin \theta_z & \cos \theta_z \end{array}\right) \times \left(\begin{array}{c} x \\ y \end{array}\right)\right] + \left(\begin{array}{c} t_x \\ t_z \end{array}\right)$

• Inconvénients
  • Non bijective.
  • Non surjective (image d'arrivée avec des trous).
• Solution
  • Pour obtenir la couleur du pixel $S'$ on calcul son antécédent $S$.
  • Parcours de l'image d'arrivée et non de l'image de départ

• Illustration

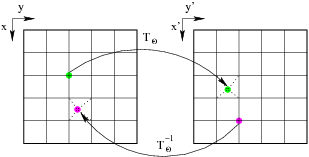
Formulation de la transformation - rotation discrète inverse

• Soient
  • $S=\left(x,y\right)^T$ un pixel de l'image de départ;
  • $S'=\left(x',y'\right)^T$ son image par la transformation dans l'image d'arrivée

$S=T_{\Theta}^{-1}(S')$.

• Formulation

$\left(\begin{array}{c} x \\ y \end{array}\right) = \left[\left(\begin{array}{cc} \cos \theta_z & -\sin \theta_z \\ \sin \theta_z & \cos \theta_z \end{array}\right) \times \left(\begin{array}{c} x'-t_x \\ y'-t_y \end{array}\right)\right] + \left(\begin{array}{c} \frac{1}{2} \\ \frac{1}{2} \end{array}\right)$

• Avantage
  • Evite le problème de la non surjectivité de la rotation.
• Remarque
  • Ajout de $\left(\frac{1}{2},\frac{1}{2}\right)^T$ => troncature vers le plus proche voisin.

Interpolation bilinéaire

• Rappel sur l'interpolation linéaire
  • Soit $c \in [a;b] \in R$ avec $f(c)$ non calculable;
  • on remplace $f$ sur $\left[a;b\right]$ par le segment $\left[AB\right]$

$f(c) \approx f(a)+(c-a) \times \frac{f(b)-f(a)}{b-a}$

• Soient $(x,y),(x,y+1),(x+1,y)$ et $(x+1,y+1)$ 4~points du plan 2D pour

• Principe de calcul de l'image de $c \in \left[x;x+1\right] \times \left[y;y+1\right]
  1. Calcul par interpolation linéaire de $f(c')$ et $f(c'')$
     • $f(c')=f(x,y)+\Delta y \times (f(x,y+1)-f(x,y))$
     • $f(c'')=f(x+1,y)+\Delta y \times (f(x+1,y+1)-f(x+1,y))$
  2. Calcul par interpolation linéaire de $f(c)$
     • $f(c)=f(c')+\Delta x \times (f(c'')-f(c'))$
  Remarque

  • $c=(x+\Delta x,y+\Delta y), c'=(x,y+\Delta y), c''=(x+1,y+\Deltay)$

Matrices de transformation

• Passage des coordonnées classiques en coordonnées homogènes

$\left(\begin{array}{c} x \\ y \end{array}\right) = \left(\begin{array}{c} x' \\ y' \\ z' \\ \end{array}\right)$

• Transformations élémentaires définies par une matrice

$\begin{array}{ccc} Identité & Rotation & Translation \\ \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) & \left(\begin{array}{ccc} \cos \theta_z & \sin \theta_z & 0 \\ -\sin \theta_z & \cos \theta_z & 0 \\ 0 & 1 &0 \end{array}\right) & \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ t_x & t_y & 1 \end{array}\right) \\ \end{array}$

• Algorithme de transformation matricielle
  1. Multiplication de matrices de transformations élémentaires.
  2. Inversion de la matrice résultante (utilisation de Gauss-Jordan).
  3. Balayage des pixels de l'image d'arrivée en multipliant à chaque fois
  sa position par la matrice inverse.

Travaux pratiques

• Mettre en oeuvre la transformation rigide en utilisant les deux formulations :
  1. rotation discrète;
  2. rotation discrète inverse.
• Utiliser comme centre de la transformation le milieu de l'image et non l'origine comme dans c'est le cas dans les formules données . Vous devrez donc légèrement modifier les formules.
• Constater que dans le premier cas on obtient un image transformée avec des trous, alors que dans le second cas l'image est correcte.
• Remarques
  • Lorsque vous aurez besoin du niveau de gris d'un pixel en dehors de l'image à transformer, vous utiliserez le noir (RGB = (0,0,0)).
  • Les deux formules font une interpolation de type plus proche voisin. On aurait pu cependant utiliser une interpolation bilinéaire.
• Illustration de la transformation rigide de centre (100,100), de vecteur translation (10,10) et d'angle 20 degrés.

Image d'origine	Transf. rotation disc.

Image d'origine	Transf. rotation disc. inverse