Introduction

Introduction aux filtres

Introduction au traitement d'images

On désigne par technique de traitement d'images toutes les techniques ayant pour but la modification des caractéristiques chromatiques des pixels des images bitmap.

Traitement d'images est souvent synonyme d'amélioration des images avec pour but l'obtention d'une plus grande lisibilité.

Il n'y a pas création d'informations, mais mise en évidence de l'information pertinente déjà présente.

Les filtres

L'utilisation de filtres est un exemple de traitement d'images en vue de leur amélioration.

Le filtrage manipule uniquement les données de l'image numérisée : meilleur rendu de l'image, ou atténuation du bruit conséquent à la numérisation, etc.

Fonctionnement des filtres

Quand on filtre, on ne s'intéresse pas à la valeur sémantique de l'image. Seul le signal (les pixels) est étudié : s'il est trop détérioré, le filtrage ne suffira pas.

Notons pour finir qu'il n'y a pas de filtre idéal, corrigeant tous les défauts : chaque filtre s'attaque à un défaut bien précis.

Les types de filtrages

Il existe deux types de filtres :

Filtrage Global (spectral)

Chaque pixel de la nouvelle image est calculé en prenant en compte la totalité des pixels de l'image de départ. Exemple : opérations sur les histogrammes, utilisant les coefficients de Fourier, etc.

Filtrage Local (matriciel)

Chaque nouveau pixel est calculé en n'utilisant qu'un voisinage du pixel correspondant dans l'image d'origine. Ces voisinages, carrés autour du pixel, sont assimilables à des matrices (appelées noyau de convolution) de taille impaire.

Filtres locaux linéaires ou pas

Parmi les filtres locaux, on distingue :

Le filtrage local linéaire

La valeur du nouveau pixel est une combinaison linéaire, éventuellement normée, des valeurs des pixels du voisinage, multipliées (terme à terme) par le noyau de convolution choisi.

Le filtrage local non-linéaire

Le filtrage n'est pas de la forme ci-dessus. Ces filtres sont plus difficiles à implanter, mais fournissent de meilleurs résultats.

Exemple d'application d'un filtre local linéaire

Par exemple, supposons que l'on ait choisi pour noyau :

$\left( \begin{array}{ccc} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \\ \end{array} \right)$

et que le block $3 \times 3$ du coin supérieur gauche de l'image (à améliorer) soit, en niveaux de gris :

$\left(\begin{array}{ccc}211 & 214 & 221 \\211 & 214 & 222 \\210 & 210 & 221 \\\end{array}\right)$

Alors le pixel $2 \times 2$ de la nouvelle image aura pour niveau de gris : $1 \times 211 + 2 \times 214 + 1 \times 221 + 2 \times 211 + ... + 1 \times 221$

Remarque sur l'exemple

On s'aperçoit que la nouvelle image aura des niveaux de gris supérieur à 255. On pourra alors rechercher le maximum $M$ de ces nouvelles valeurs, et diviser tous les niveaux de gris par $M$.

Pour les noyaux de convolutions ayant des valeurs négatives, on peut trouver des niveaux de gris négatifs. Une homothétie-translation permettra de se ramener à des niveaux entre 0 et 255.

Enfin, pour les pixels au bord de l'image, on peut (par exemple) fixer les éléments non-définis de leurs voisinages à 0.

Le spectre

On appelle spectre d'une image, la courbe de répartition des couleurs d'une image : niveau de gris en x, nombre de pixels en y.

Sur une image noir et blanc (à niveaux de gris), il existe un seul spectre.

Sur une image en couleurs, on peut calculer un spectre par teinte de base ou utiliser la moyenne des trois composantes pour chaque pixel.

Spectre et module Image

Pour obtenir le spectre, après avoir ouvert une image :

  >>> import Image
  >>> toto=Image.open('monImage.jpg','r')
  >>> toto.histogram()

Pour une visualisation graphique :

  >>> from pylab import plot,show
  >>> plot(toto.histogram()) 
  >>> show()

Histogrammes d'une image RGB

Selon le mode de l'image (niveaux de gris, RGB, etc.), le vecteur renvoyé par toto.histogram() n'aura pas la même taille.

Dans le cas d'une image RGB, ce vecteur a 256*3 = 768 éléments, correspondant à la concaténation des histogrammes en rouge, vert et bleu.

Pour n'afficher que la partie vert, par exemple :

  >>> plot(toto.histogram()[255:2*255])
  >>> show()

Enfin, toto.getextrema() permet de récupérer les valeurs extrémales de l'histogramme, par bande.

Opérations de base

Opérations composante par composante

On peut effectuer des opérations composante par composante (sur le rouge, le vert et le bleu par exemple) sur les images :

Addition

p(x,y) = p1(x,y)+p2(x,y) (seuillage à la valeur maximum, par exemple 255 dans le RGB)

Soustraction

p(x,y) = p1(x,y)-p2(x,y) (seuillage à la valeur minimum)

Opérations bit par bit

On peut aussi effectuer des opérations bit par bit (sur les valeurs binaires des pixels) sur les images :

et

p(x,y) = p1(x,y) and p2(x,y) (le et booléen)

ou

p(x,y) = p1(x,y) or p2(x,y) (le ou booléen)

ou exclusif

p(x,y) = p1(x,y) xor p2(x,y)

négation

p(x,y) = not p1(x,y) (la négation booléenne)

Travaux pratiques

1. Réalisez chacune des opérations de base suivantes.
2. On pourra faire une interface graphique.

Filtrage global (spectral)

Le filtre négation

Présentation

Effectuer un filtrage spectral consiste à modifier, selon une fonction $f$(teinte), la teinte de chaque pixel de l'image de manière à modifier son spectre.

Négation d'une image

Par exemple, pour la négation d'une image RGB, la teinte des pixels est modifiée suivant la fonction $f(x) = 255-x$ :

Réalisation du filtre négation

Réalisons un tel filtre...

1. On ouvre notre image, que l'on stocke dans la variable toto.
2. On crée une fonction negat, qui correspond à $f(x)=255-x$.
3. Puis on parcourt chaque pixel de notre image (toto.size[0] est le nombre de colonnes de pixels, toto.size[1] le nombre de lignes)...
4. On récupère le triplet RGB du pixel, et on applique notre fonction negat à chaque composante.

Code du filtre négation

  >>> toto=Image.open('03.jpg','r')

  ...     return 255-x
  ...
  >>> for k in range(toto.size[0]):
  ...     for l in range(toto.size[1]):
  ...         X=toto.getpixel((k,l))
  ...         toto.putpixel((k,l),(negat(X[0]),negat(X[1]),negat(X[2])))
  ...
  >>>toto.show()

Exemple du filtre négation

L'assombrissement

Assombrissement d'une image

Passons à l'assombrissement d'une image...

La teinte des pixels est déplacée de manière à rapprocher les composantes RGB de leur minimum, pour assombrir l'image.

La fonction est du genre $f(x) = \lfloor 255 \left( \frac{x}{255} \right)^2 \rfloor$.

Fonction d'assombrissement

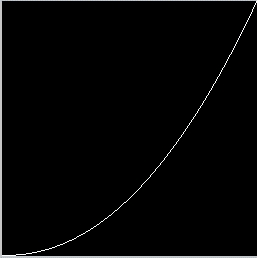
Cela revient à tasser le spectre vers la gauche.

Exemple du filtre d'assombrissement

L'éclaircissement

Eclaircissement d'une image

Pour éclaircir une image, on procède comme précédemment, sauf que les composantes RGB de l'image sont rapprochées de leur maximum.

La fonction est du genre $f(x) = \lfloor 255 \sqrt{ \frac{x}{255}} \rfloor$.

Fonction d'éclaircissement

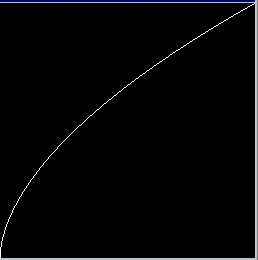
Cela revient à tasser le spectre vers la droite.

Exemple du filtre d'éclaircissement

Diminution du contraste

Diminution du contraste

Pour diminuer le contraste on rapproche les composantes RGB de leur moyenne.

La fonction est du genre $f(x) = \lfloor 127+127 \times \left( \frac{x-127}{127} \right)^3 \rfloor$.

Fonction de diminution du contraste

Une fonction pour diminuer le contraste...

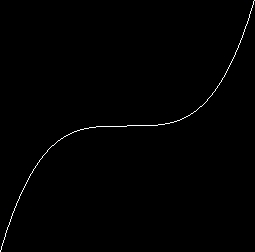
Cela revient à tasser le spectre vers le centre.

Exemple de diminution du contraste

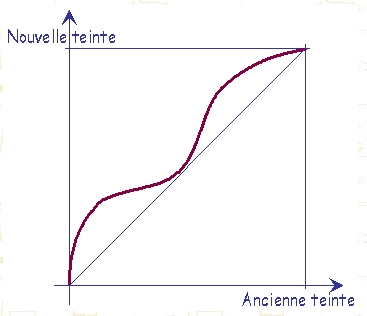
Augmentation du contraste

Augmentation du contraste

Pour augmenter le contraste, on éloigne les composantes RGB de leur moyenne (ellles sont rapprochées de leurs extrema).

La fonction est du genre $f(x) = \lfloor 127+127 \times \sqrt{ \frac{x-127}{127}} \rfloor$.

où $\sqrt{X}$ désigne ici la racine cubique.

Fonction d'augmantation du contraste

Une fonction pour augmenter le contraste...

Cela revient à tasser le spectre vers les bords.

Travaux pratiques

1. Réalisez chacun des précédents filtres, avec les fonctions proposées.
2. Créez vos propres filtres (mise en valeur de la composante Vert, seuillage d'une composante, conversion en noir et blanc, etc.)
3. Améliorer les fonctions des filtres de contrastes, en utilisant la valeur moyenne par bande (RGB), plutôt que 127. On pourra regarder le TP de probabilités : Comment manipuler ses notes à souhait.
4. Faire une interface graphique, demandant à l'utilisateur de sélectionner son image, et quel algorithme appliquer.