Présentation

La transformée en cosinus discrète, ou dct (1974) est une transformée permettant la conversion d'un signal numérique en ses composantes fréquentielles.

Elle est grandement utilisée pour la compression de données multimedia : les formats JPEG (image), MPEG (vidéo) et CCITT H.261 (le Px64 des téléconférences) sont basés sur cette DCT.

DCT une dimension

Définition

La définition

La dct une dimension d'une liste $s(x)_{x=0,..,n-1}$ de $n$ réels est définie par $S_s(u) = \frac{2}{\sqrt{2n}} C(u) \sum_{x=0}^{n-1} s(x) cos \frac{(2x+1)u\pi}{2n}, u=0,..,n-1$

où $C(u) = \left\{ \begin{array}{ll} \frac{1}{\sqrt{2}} & \textrm{si } u=0 \\ 1 & \textrm{sinon } \end{array}\right.$

La valeur de $S_s$ dépend donc de la liste de nombres $s$ dont elle est la transformée.

Travaux pratiques

1. Créer la fonction $C(u)$.
2. Utiliser cette dernière pour définir la fonction DCT, qui recevra $(s,u)$ et renverra $S_s(u)$.

Version matricielle

Vers une version matricielle

$S(u)$ est ainsi le produit scalaire entre $s(x)$ et le vecteur $V(u) = \frac{2}{\sqrt{2n}} C(u) \left( cos\frac{u\pi}{2n}, cos\frac{3u\pi}{2n},cos\frac{5u\pi}{2n}, ..., cos\frac{(2n-1)u\pi}{2n} \right)^T$ où la famille des vecteurs $V(u)_{u=0, ..., n-1}$ forme une base orthonormée de $\mathbb{R}^n$.

En d'autres termes, la dct $S$ est égale au produit matriciel $S = s*V$, où $V$ est la matrice (orthogonale) dont le $i$^ième vecteur colonne est $V(i)$.

Travaux pratiques

1. Définir la fonction $V(u)$.
2. Faire une nouvelle fonction DCT, en utilisant ce qui précède, et le produit scalaire. On pourrait utiliser numpy ou sympy pour le produit scalaire, ou encore le redéfinir à la main;

Les fréquences

Chaque vecteur de base $V(i)$ correspond à une sinusoïde d'une fréquence déterminée.

Représentons cela, avec le bout de code suivant :

  >>> from math import cos, pi, sqrt
  >>> def C(u): 
  ...     return 1 if u != 0 else 1./sqrt(2)
  ... 
  >>> def V(u):
  ...     return [2./sqrt(2*8)*C(u)*cos((2*k+1)*u*pi/(2.*8))\
  ...                  for k in range(8)]
  ... 
  >>> import matplotlib.pyplot as plt
  >>> fig = plt.figure()
  >>> for k in range(1,9):
  ...     fig.add_subplot(8,1,k)
  ...     plt.plot(range(8), V(k-1))
  ... 

On trouve alors des sinusoïdes (discrètes) aux différentes fréquences :

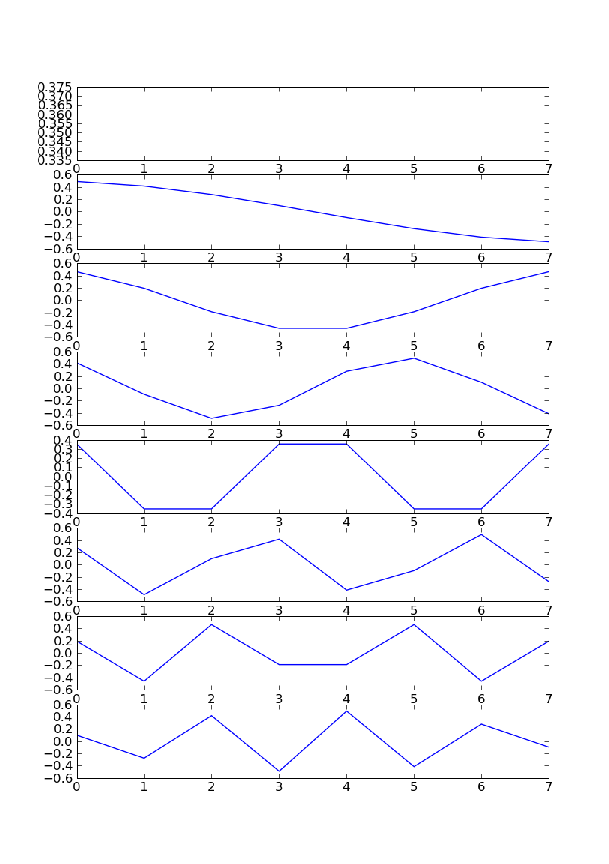
DCT inverse

Définition

On peut retrouver $s$ à partir de sa DCT $S$ en appliquant la transformée en cosinus discrète inverse (IDCT) :

$s(x) = \frac{2}{\sqrt{2n}} \sum_{u=0}^{n-1} C(u) S(u) \cos \frac{(2x+1)u\pi}{2n}, x=0,..., n-1$

où $C(u)$ a été défini précédemment.

Ainsi, $s$ est une combinaison linéaire des vecteurs de base $V(u)$ : la $k$^ième coordonnées de $s$ dans cette base peut être vue comme la quantité de présence de chaque fréquence dans l'entrée $s$.

Travaux pratiques

1. Définir la DCT inverse.
2. Vérifier, sur des exemples, qu'elle est effectivement l'inverse de la DCT.

DCT deux dimensions

Motivations

La dct 1D sert lorsque l'on manipule des signaux à une dimension, tels qu'un enregistrement sonore.

Pour analyser des signaux 2D, tels que les images, il faut donc une version 2D de la dct.

Définition

La formule

Pour obtenir la dct 2D d'une matrice de taille $n \times m$,

• on applique une dct 1D à chaque ligne de $s$,
• on applique une autre dct 1D à chaque colonne du résultat.

On peut donc l'obtenir ainsi

$S(u,v) = \frac{2}{\sqrt{nm}} C(u) C(v) \sum_{y=0}^{n-1} \sum_{x=0}^{n-1} s(x,y) cos \frac{(2x+1)u \pi}{2n} cos \frac{(2y+1)v \pi}{2m}$ où $u=0, ..., n$, et $v=0, ..., m$.

Par cette transformée, l'image d'origine est vue comme une combinaison linéaire de $n \times m$ matrices de base, qui sont (pour $m = n = 8$)...

On généralise ainsi le cas 1D. On constate que l'on peut caractériser chacune de ces matrices de base par un couple de fréquences : horizontale et verticale.

Elles ont été rangées ci-dessus dans le sens des fréquences croissantes.

Utilité

Toute image peut se décomposer en blocs $8 \times 8$, et chacun de ces blocs peut s'écrire comme une combinaison linéaire des blocs de base ci-dessus (chaque coefficient décrit la quantité du bloc de base associé dans l'image étudiée).

Exemple

  from numpy import *
  A = array([ [0,0,0,1,0,0,0,0],
              [0,0,1,0,1,0,0,0],
              [0,0,1,0,1,0,0,0],
              [0,1,0,0,0,1,0,0],
              [0,1,1,1,1,1,0,0],
              [0,1,0,0,0,1,0,0],
              [0,1,0,0,0,1,0,0] ])
  import Image as im
  dd = im.new('1',(8,8))
  dd.putdata(A.flatten())
  dd.show()

Travaux pratiques

Définir cette DCT pour la dimension 2.