WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
La coloration des graphes
Introduction du problème
Un problème historique
Une question datant de la fin XIXe, reliée à la coloration de graphes planaires, est devenue célèbre sous le nom de problème des quatre couleurs : suffit-il de quatre couleurs pour dessiner n'importe quelle carte géographique ?
Formulation en théorie des graphes
Ce problème a une formulation dans le langage des graphes : y a-t-il toujours, dans un graphe planaire, une application de l'ensemble $S$ des sommets vers un ensemble de cardinal 4, telle que deux sommets « adjacents » admettent toujours des images distinctes ?
Théorème (Théorème des quatre couleurs)
On peut colorer les sommets d'un graphe planaire (sans boucles) en utilisant au plus quatre couleurs de telle sorte que toutes les arêtes aient des extrémités de couleurs différentes.
Cette conjecture a été formulée pour la première fois par l'Écossais Francis Guthrie en 1852. Il était alors question de coloration de carte de géographie (voir exercice ci-dessous).
La preuve de ce théorème n'arriva qu'en... 1976, grâce à Kenneth Appel et Wolfgang Haken. La démonstration fit grand bruit car c'est le premier théorème de l'histoire des mathématiques qui a nécessité l'usage systématique de l'ordinateur.
La communauté mathématique se divisa alors en deux camps : ceux pour qui le théorème des quatre couleurs était définitivement démontré, et ceux pour qui tout restait à faire.
Le résultat de Appel et Haken est donc délicat à prouver. On verra cependant, dans les prochaines sections, qu'un certain nombre de résultats sur le nombre de couleurs nécessaires à la coloration, peuvent s'obtenir sans trop de difficultés. Le problème de la coloration des arêtes sera aussi introduit.
Coloration des sommets
Afin d'obtenir des encadrements du nombre de couleurs, il nous faut exprimer rigoureusement le problème de coloration en termes issus de la théorie des graphes...
Notion de stabilité
Présentation
On rappelle que l'on appelle stable d'un graphe $G = (S, A)$ tout sous-graphe sans arête obtenu en enlevant des sommets à $G$ (et uniquement leurs arêtes incidentes).
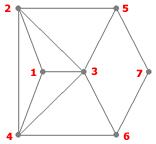
Par exemple, dans le graphe suivant, on peut obtenir un stable en enlevant les sommets {1, 2, 4} : le graphe résultant est sans arête.

Définition (Nombre de stabilité)
Le nombre de sommets du plus grand stable est le nombre de stabilité de $G$
Notation: On le note $a(G)$.
Travaux pratiques
Faire une fonction qui retourne le nombre de stabilité d'un graphe donné, en exploitant les fonctions que vous avez déjà précédemment écrites.
Correction
from networkx import *
from itertools import combinations
from copy import deepcopy
G=Graph()
G.add_edges_from([(2,3),(3,4),(3,1),(1,4),(1,5),(4,5)])
partitions = sum([list(combinations(G.nodes(),k)) for k in range(1,6)],[])
stables=[]
for k in partitions:
H=deepcopy(G)
H.remove_nodes_from(k)
if len(H.edges())==0:
stables.append(len(H.nodes()))
print max(stables)
Le problème de coloration
Définition (Coloration des sommets d'un graphe)
La coloration des sommets d'un graphe consiste à affecter à tous les sommets de ce graphe une couleur de telle sorte que deux sommets adjacents ne portent pas la même couleur.
Théorème
Une coloration avec $k$ couleurs est une partition de l'ensemble des sommets $S$ en $k$ stables.
Définition (Nombre chromatique)
Le nombre chromatique du graphe $G$ est le plus petit entier $k$ pour lequel il existe une partition de $V$ en $k$ sous-ensembles stables. C'est le nombre de couleurs minimal pour colorier un graphe.
Notation: Ce nombre chromatique est noté $g(G)$.
Exemple : Sur le graphe ci-dessous, on a eu besoin de trois couleurs pour colorer les sommets de sorte que deux sommets adjacents ont des couleurs différentes.

Remarque : La coloration minimale n'est pas forcément unique. Par exemple, ci-dessus, le sommet 2 aurait aussi pu être vert.
Encadrement du nombre chromatique
Majoration
On rappelle que le degré $d(x)$ d'un sommet $x$ est, par définition, son nombre d'arêtes. On a les deux majorations suivantes...
Théorème
$g(G) \leqslant r + 1$, où $r$ est le plus grand degré de ses sommets.
Preuve : Soit un graphe et $r$ le degré maximum de ses sommets. Donnons-nous une palette de ($r + 1$) couleurs. Pour chaque sommet du graphe on peut tenir le raisonnement suivant :
- ce sommet est adjacent à $r$ sommets au plus,
- le nombre de couleurs déjà utilisées pour colorer ces sommets est donc inférieur ou égal à $r$.
Il reste donc au moins une couleur non utilisée dans la palette, avec laquelle nous pouvons colorer notre sommet.
Théorème
$g(G) \leqslant n + 1 - a(G)$
Preuve : Considérons $S$ un stable de $V$ de cardinal $a(G)$ : une coloration possible des sommets consiste à colorer les sommets de $S$ d'une même couleur et les $n-a(G)$ autres sommets de couleurs toutes différentes.
On en déduit que $g(G) \leqslant 1+(n-a(G))$.
Minoration
On a d'autres résultats, concernant la minoration...
Théorème
Le nombre chromatique d'un graphe est supérieur ou égal à celui de chacun de ses sous-graphes.
Preuve : Ce résultat découle de la définition même du nombre chromatique.
Théorème
$g(G) \geqslant w(G)$, où $w(G)$ désigne l'ordre de la plus grande clique de $G$.
Preuve : Puisque, par définition, dans une clique d'ordre $m$, tous les sommets sont adjacents entre eux, il faudra $m$ couleurs pour colorier ce sous-graphe. Donc, forcément, le nombre chromatique du graphe sera supérieur ou égal à l'ordre de sa plus grande clique.
Exemple : Dans le graphe précédant, on a utilisé trois couleurs :

On ne peut faire mieux, à cause des cliques 1-4-5 et 1-3-4.
Remarque : Tout graphe contenant $K_3$ nécessite ainsi au moins 3 couleurs.
Travaux pratiques
Ecrire une fonction qui reçoit un graphe, et qui retourne un encadrement pour son nombre chromatique. On pourra renvoyer un couple (borne min, borne max).
Algorithme de coloration de Welsh et Powell
Cet algorithme couramment utilisé permet d'obtenir une assez bonne coloration d'un graphe, c'est-à-dire une coloration n'utilisant pas un trop grand nombre de couleurs. Cependant il n'assure pas que le nombre de couleurs utilisé soit minimum (et donc égal au nombre chromatique du graphe).
- Étape 1
Classer les sommets du graphe dans l'ordre décroissant de leur degré, et attribuer à chacun des sommets son numéro d'ordre dans la liste obtenue.
(Une manière de faire ceci, à décortiquer :
sorted(G.degree().items(), key = lambda x:x[1], reverse = True)
)
- Étape 2
En parcourant la liste dans l'ordre, attribuer une couleur non encore utilisée au premier sommet non encore coloré, et attribuer cette même couleur à chaque sommet non encore coloré et non adjacent à un sommet de cette couleur.
- Étape 3
S'il reste des sommets non colorés dans le graphe, revenir à l'étape 2. Sinon, la coloration est terminée.
Travaux pratiques
Programmer l'algorithme de coloration de Welsh et Powell, puis l'utiliser pour répondre aux exercices suivants.
Exercice : On a vu que tout graphe contenant un triangle ($K_3$) ne peut pas être coloré en moins de trois couleurs.
- Construire un graphe sans $K_3$ qui nécessite également trois couleurs.
- Comment, à partir du graphe précédent, construire un graphe sans $K_4$ nécessitant 4 couleurs ?
- Un graphe sans $K_5$ nécessitant 5 couleurs ?
Exercice : Déterminez le nombre chromatique de ce graphe :
Exercice : Sept élèves, désignés par A, B, C, D, E, F et G, se sont rendus à la bibliothèque aujourd'hui. Le tableau suivant précise «qui a rencontré qui» (la bibliothèque étant petite, deux élèves présents au même moment se rencontrent nécessairement...).
| $l'élève $ | $ A $ | $ B $ | $ C $ | $ D $ | $ E $ | $ F $ | $ G$ |
| $a rencontré $ | $ D,E $ | $ D,E,F,G $ | $ E,G $ | $ A,B,E $ | $ A,B,C,D,F,G $ | $ B,E,G $ | $ B,C,E,F$ |
De combien de places assises doit disposer la bibliothèque pour que chacun ait pu travailler correctement au cours de cette journée?
Exercice : A, B, C, D, E, F, G et H désignent huit poissons. Dans le tableau ci-dessous, une croix signifie que les poissons ne peuvent pas cohabiter dans un même aquarium :
| $ A $ | $ B $ | $ C $ | $ D $ | $ E $ | $ F $ | $ G $ | $ H $ | |
| $A $ | $ $ | $ \times $ | $ \times $ | $ \times $ | $ $ | $ $ | $ \times $ | $ \times $ |
| $B $ | $ \times $ | $ $ | $ $ | $ $ | $ \times $ | $ \times $ | $ \times $ | $ $ |
| $C $ | $ \times $ | $ $ | $ $ | $ \times $ | $ $ | $ \times $ | $ \times $ | $ \times $ |
| $D $ | $ \times $ | $ $ | $ \times $ | $ $ | $ \times $ | $ $ | $ $ | $ \times $ |
| $E $ | $ $ | $ \times $ | $ $ | $ \times $ | $ $ | $ \times $ | $ \times $ | $ $ |
| $F $ | $ $ | $ \times $ | $ \times $ | $ $ | $ \times $ | $ $ | $ $ | $ $ |
| $G $ | $ \times $ | $ \times $ | $ \times $ | $ $ | $ \times $ | $ $ | $ $ | $ $ |
| $H $ | $ \times $ | $ $ | $ \times $ | $ \times $ | $ $ | $ $ | $ $ | $ $ |
Quel nombre minimum d'aquariums faut-il?
Exercice : Un lycée doit organiser les horaires des examens. On suppose qu'il y a 7 épreuves à planifier, correspondant aux cours numérotés de 1 à 7 et que les paires de cours suivantes ont des étudiants communs: 1 et 2, 1 et 3, 1 et 4, 1 et 7, 2 et 3, 2 et 4, 2 et 5, 2 et 7, 3 et 4, 3 et 6, 3 et 7, 4 et 5, 4 et 6, 5 et 6, 5 et 7 et enfin 6 et 7. Comment organiser ces épreuves de façon qu'aucun étudiant n'ait à passer deux épreuves en même temps et cela sur une durée miminale?
Exercice : Sept agences de voyage romaines proposent des visites de monuments et lieux touristiques: le Colisée, le Forum romain, le musée du Vatican et les thermes de Caracalas. Un même lieu ne peut être visité par plusieurs groupes de compagnies différentes le même jour. La première Compagnie fait visiter uniquement le Colisée; la seconde le Colisée et le musée du Vatican; la troisième les thermes de Caracalas; la quatrième le musée du Vatican et les thermes de Caracalas; la cinquième le Colisée et le Forum romain; la sixième le Forum romain et les thermes de Caracalas; la septième le musée du Vatican et le forum romain. Ces agences peuvent-elles organiser les visites sur les trois premiers jours de la semaine?
Exercice : Utilisez l'algorithme de coloration de Welsh et Powell pour colorer les graphes des exercices précédents.
Exercice : Exprimez la résolution d'un Sudoku classique en termes de coloration de graphe. Décrivez le graphe (nombre de sommets, nombre d'arêtes, etc.). Combien faut-il de couleurs?
Coloration des arêtes
Présentation du problème
La coloration des arêtes d'un graphe consiste à affecter à toutes les arêtes de ce graphe une couleur de telle sorte que deux arêtes adjacentes ne portent pas la même couleur.
Définition (Indice chromatique)
L'indice chromatique du graphe $G$ est le plus petit entier $k$ pour lequel il existe une coloration des arêtes.
Notation: On le note $c(G)$.
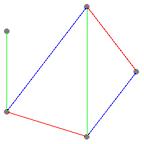
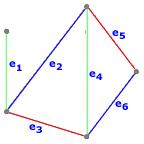
Exemple : Sur le graphe ci-dessous, on a eu besoin de trois couleurs pour colorer les arêtes de sorte que deux arêtes adjacentes ont des couleurs différentes.
Lien avec la coloration des sommets
Présentation
Pour colorer les arêtes d'un graphe, on peut se ramener au problème de la coloration des sommets. Il suffit pour cela de travailler non pas sur le graphe lui-même, mais sur le graphe adjoint, noté G', et que l'on définit ainsi:
- à chaque arête de G = (V, E) correspond un sommet de G' = (E, F)
- deux sommets de G' sont reliés par une arête si les deux arêtes correspondantes de G sont adjacentes.
On peut ensuite appliquer par exemple l'algorithme de Welsh et Powell sur le graphe G' pour colorer ses sommets. Une fois cela fait, on colorera les arêtes de G de la même couleur que les sommets correspondants de G'.
Exemple de coloration d'arêtes
Un graphe G :
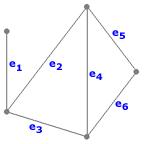
Son graphe adjoint G'

Coloration des sommets de G'

Coloration des arêtes de G
Travaux pratiques
- Faire un programme qui construit le graphe adjoint d'un graphe donné
- Faire une fonction qui produit un encadrement de l'indice chromatique d'un graphe
- Résoudre l'exercice suivant.
Exercice : Dans un tournoi d'échecs, chaque engagé doit rencontrer tous les autres. Chaque partie dure une heure.
Déterminer la durée minimum du tournoi dans le cas où le nombre d'engagés est 3, 4, 5 ou 6.