WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Les graphes hamiltoniens
Circuit hamiltonien
Les dodécaèdres de Hamilton
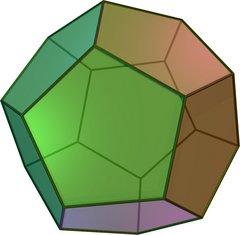
Le dodécaèdre est à l'origine d'un autre problème célèbre, dû à Hamilton : comment passer une, et une seule fois, par chacun des sommets du dodécaèdre, de telle manière que le dernier sommet visité est aussi le premier.
Définition
Définition (Circuit et graphes hamiltoniens)
Un circuit hamiltonien est un circuit qui passe par tous les sommets du graphe, une et une seule fois. Un graphe possédant un tel circuit est qualifié d'hamiltonien.
Remarque : C'est un circuit : le sommet de départ doit aussi être le sommet d'arrivée.
Exemple : Les graphes complets $K_n$ sont hamiltoniens, pour tout $n$.
Preuve : On peut inscrire $K_n$ dans un polygone régulier à $n$ sommets : il suffit alors de parcourir ce polygone, sommet par sommet, dans le sens trigonométrique par exemple, jusqu'à retrouver son point de départ.
Remarque : Dans le cas des graphes orientés (voir plus loin), on parle de graphe hamiltonien s'il est possible de trouver un cycle passant une et une seule fois par tous les sommets.
Remarque : Il peut y avoir plusieurs circuits hamiltoniens dans un graphe hamiltonien.
Le problème de la caractérisation des graphes Hamiltoniens n'est pas aussi simple que celui des graphes Eulériens. On peut cependant énoncer quelques conditions, respectivement nécessaires, puis suffisantes, pour qu'un graphe le soit...
Conditions nécessaires
Théorème
Un graphe hamiltonien d'ordre $n \geqslant 3$ ne possède pas de sommet de degré 1.
Preuve : Si un sommet $s$ est de degré 1, il est connecté à un (unique) autre sommet $s'$, qui sera forcément parcouru deux fois (pour aller en $s$, et pour en sortir).
Remarque : $K_2$ est hamiltonien, et a tous ses sommets d'ordre 1...
Théorème
Si un graphe hamiltonien possède un sommet de degré 2, alors les deux arêtes incidentes à ce sommet doivent faire partie du cycle hamiltonien.
Preuve : Supposons que $s$ est de degré 2, connecté à $s_1$ par l'arête $a_1$, et à $s_2$ par $a_2$. On est arrivé à $s$ à partir d'une arête, mettons $a_1$ ; si on réempruntait $a_1$ pour sortir de $s$, alors on repasserait par $a_1$, ce qui est impossible.
Conditions suffisantes
Théorème (Théorème de Ore)
Soit G = (V, E) un graphe simple d'ordre $n\geqslant 3$. Si pour toute paire {x,y} de sommets non adjacents, on a $d(x) + d(y) \geqslant n$, alors G est hamiltonien.
Théorème (Corollaire de Dirac)
Soit G = (V, E) un graphe simple d'ordre $n\geqslant 3$. Si pour tout sommet x de G, on a $d(x) \geqslant n/2$, alors G est hamiltonien.
Preuve : En effet, un tel graphe vérifie les conditions du théorème précédent. Si x et y ne sont pas adjacents, on a bien : $d(x) + d(y) \geqslant n/2 + n/2 = n$
Travaux pratiques
- Faire une fonction qui reçoit un graphe, et qui dit s'il peut ou non être hamiltonien, à partir des résultats évoqués ci-dessus
- Faire une fonction qui reçoit une liste d'arêtes et un graphe, et qui dit si cette liste est un circuit hamiltonien dans ce graphe
- Dessinez un graphe d'ordre au moins 5 qui est...
- hamiltonien et eulérien,
- hamiltonien et non eulérien,
- non hamiltonien et eulérien,
- non hamiltonien et non eulérien.
Le problème du voyageur de commerce
Trouver un cycle hamiltonien pour un graphe donné est un problème difficile sur le plan algorithmique -- de type NP-complet --, relié au problème dit du voyageur de commerce : un voyageur de commerce doit visiter un ensemble de villes, en minimisant son temps de parcours.
Ce problème se formalise aisément en théorie des graphes :
- Les villes sont les sommets d'un graphe pondéré.
- Les arêtes correspondent aux routes reliant ces villes.
- La pondération correspond soit à la distance entre deux ville (en kilomètres), soit à la durée nécessaire pour passer d'une ville à l'autre.
- Ce graphe peut être orienté, si l'on souhaite intégrer des routes à sens unique.
On cherche alors à visiter tous les sommets du graphe (i.e. toutes les villes) en minimisant le « poids » du parcours (la distance parcourue, ou le temps total).
Le problème du voyageur de commerce correspond donc à la recherche d'un cycle hamiltonien de poids minimal, dans un graphe pondéré complet. Ce problème est NP-complet, donc impossible à résoudre exactement quand le nombre de villes est grand.