WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Chaînes et circuits eulériens
Graphes connexes
Le problème des graphes eulériens est relié à la connexité d'un graphe, un graphe étant connexe quand pour tout couple de sommets, on peut trouver un chemin passant du premier sommet au second. On voit ici comment manipuler de tels graphes avec networkx.
Prise en main avec networkx
- Faire évaluer par Networkx la connexité des deux graphes suivants, en exploitant la fonction is_connected(G) de NetworkX;
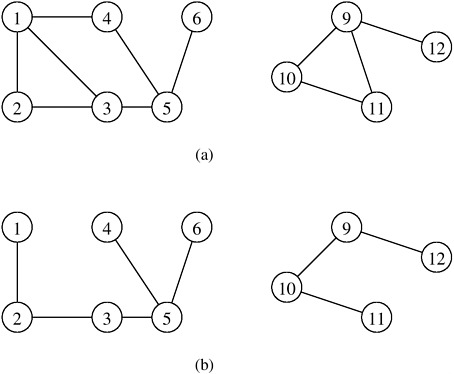
- Faire construire la liste des composantes connexes en exploitant la fonction connected_component_subgraphs(G) de NetworkX;
Le problème des cavaliers
Sur un échiquier 3x3, les deux cavaliers noirs sont placés sur les cases a1 et c1, les deux cavaliers blancs occupant les cases a3 et c3.
- Construire le graphe permettant de déterminer les mouvements qui autoriseront les cavaliers blancs à prendre les places des cavaliers noirs, et vice versa.
- Faire construire les plus courts chemins résolvant la contrainte d'échange sans tenir compte que sur une case, il ne peut y avoir une seule pièce.
- Ces chemins sont-ils compatibles avec la contrainte d'unicité de pièce sur une case ?
Lien vers Une solution possible.
Circuits eulériens
On rappelle des éléments de cours sur les circuits eulériens, et on les étudie avec networkx.
Introduction : les ponts de Königsberg
La question à l'origine de la théorie des graphes est due à Euler, en 1736 : dans cette partie de la ville de Königsberg :
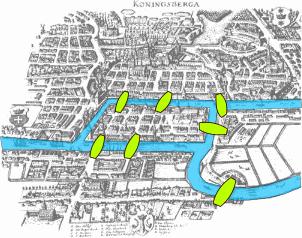
Peut-on, lors d'une promenade, revenir à notre point de départ en empruntant une, et une seule fois, chaque pont ?
Pour y répondre, Euler a introduit le graphe suivant (les arcs symbolisent les ponts ; les sommets, les quatre zones terrestres) :

Le problème de départ se ramène alors à la question suivante : peut-on trouver un circuit permettant d'emprunter une, et une seule fois chaque arête, en retournant à son point de départ ?
La réponse, dans ce cas particulier, est non : comme
- le point de départ $s$ est aussi le point d'arrivée,
- on ne peut pas emprunter deux fois une même arête,
on en conclut forcément que le degré de $s$ est pair. Or, dans le graphe ci-dessus, tous les sommets ont un degré impair.
Travaux pratiques
Faire une résolution numérique du problème des ponts de Königsberg à l'aide de Networkx:
- Commencer par saisir le graphe
- Obtenir toutes les listes ordonnées d'arêtes possibles (sans répétition)
- Supprimer, dans la liste ci-dessus, les listes d'arêtes ne correspondant pas à des chemins possibles (on ne peut sauter d'un sommet à un autre sans emprunter une arête les faisant adjacents)
- Conclure
Rappels de définitions
Ce problème, introduit par Euler, conduit aux définitions suivantes...
Définition (Chaîne eulérien)
On appelle chaîne eulérienne une chaîne contenant une et une seule fois toutes les arêtes du graphe.
Définition (Circuit eulérien)
On appelle circuit eulérien un circuit contenant une et une seule fois toutes les arêtes du graphe.
Remarque : On n'a plus affaire à une chaîne, mais à un circuit : le point de départ et celui d'arrivée coïncident.
Définition (Graphe eulérien)
Un graphe eulérien est un graphe possédant un circuit eulérien.
Remarque : On peut passer plusieurs fois par un sommet donné, pourvu que les arêtes empruntées soient toutes différentes.
Travaux pratiques
- Faire une fonction qui dit si un circuit donné est eulérien ou non. Cette fonction recevra un graphe et un circuit.
- Faire une fonction qui retourne tous les circuits d'un graphe donné
- A partir des deux fonctions précédentes, faire une fonction qui dit si un graphe est ou non eulérien. (La complexité de cette fonction est très mauvaise).
- Résoudre à nouveau le problème des ponts de Königsberg.
Résultat d'Euler
Le résultat
Du problème initial d'Euler, on peut en déduire le résultat suivant (rappelons qu'il s'agit ici de graphes non orientés)...
Théorème
Il y a équivalence entre :
- posséder une chaîne eulérienne,
- être connexe, avec O ou 2 sommets de degré impair.
De plus, s'il n'y a pas de sommet de degré impair, alors le graphe est Eulérien.
Preuve : En parcourant un chemin ou un circuit, pour chaque sommet visité, on utilise une arête pour arriver à ce sommet et une arête pour en repartir, ces deux arêtes ne devant plus être utilisées par la suite.
Le nombre d'arêtes utilisables en ce sommet diminue donc de deux. Si un sommet est d'ordre impair, une de ses arêtes aboutissant à ce sommet doit donc être soit sur la première arête d'un chemin, soit sur la dernière.
Un chemin n'ayant que deux extrémités, le nombre de sommets d'ordre impair ne peut excéder deux.
Exercice : Soit G un graphe connexe non eulérien. Est-il toujours possible de rendre G eulérien en lui rajoutant un sommet et quelques arêtes?
Réponse : Oui. Quand on ajoute un nouveau sommet, son nombre d'arêtes doit être pair, pour ne pas poser de nouveaux problèmes. On peut donc ainsi corriger le problème d'imparité pour un nombre pair de sommets : en reliant chaque couple de deux sommets de degré impairs, à un sommet que l'on crée uniquement pour ce couple. Or, tout graphe simple possède un nombre pair de sommets de degré impair...
Exercice : les dominos
Exercice : On considère des dominos dont les faces sont numérotées 1, 2, 3, 4 ou 5.
- En excluant les dominos doubles, de combien de dominos dispose-t-on ?
- Montrez que l'on peut arranger ces dominos de façon à former une boucle fermée (en utilisant la règle habituelle de contact entre les dominos).
- Pourquoi n'est-il pas nécessaire de considérer les dominos doubles ?
- Si l'on prend maintenant des dominos dont les faces sont numérotées de 1 à n, est-il possible de les arranger de façon à former une boucle fermée ?
Réponse :
- On dispose de 4+3+2+1 = 10 dominos.
- Considérons $K_5$, le pentagramme complet. A l'arête $(1,2)$, par exemple, est associée le domino $(1,2)$. Arriver à constituer une boucle fermée de dominos revient donc à trouver un circuit eulérien dans $K_5$. C'est possible : $K_5$ est connexe, avec tous ses sommets de degré pairs.
- Considérer les dominos doubles revient à placer une boucle à chaque sommet de $K_5$. On ne change pas sa connexité, ni la parité de ses sommets.
- On obtient, dans ce cas, $K_n$, dont chaque sommet a pour degré $n-1$. Pour arriver à constituer une boucle fermée, il faut donc (et il suffit) que $n$ soit impair.
Travaux pratiques
On considère des dominos dont les faces sont numérotées 1, 2, 3, 4 ou 5. On souhaite arranger ces dominos de façon à former une boucle fermée (en utilisant la règle habituelle de contact entre les dominos).
- Comment représenter le problème par un graphe ? De quel problème s'agit-il ?
- Construire le graphe associé à ce problème. Ne pas oublier d'ajouter les paires de doubles.
- Exploiter la méthode eulerian_circuit(G, source=None) de networkx pour répondre au problème.
- Si l’on prend maintenant des dominos dont les faces sont numérotées de 1 à $n$, est-il possible de les arranger de façon à former une boucle fermée ? Essayer avec $n=6$,$n=6$, $n=7$,$n=8$ par exemple et proposer une conjecture.
Problèmes d'existence de chemin
Le problème des graphes eulériens revient à chercher si un chemin particulier existe. Voici, deux autres problèmes (travaux pratiques) d'existence d'un chemin entre deux sommets donnés.
Le loup, la chèvre et le chou fleur
Un loup, une chèvre et un chou fleur se trouvent sur la rive gauche d’un fleuve ; un passeur souhaite les transporter sur la rive droite mais, sa barque étant trop petite, il ne peut transporter qu’un seul d’entre eux à la fois.
Comment doit-il procéder afin de ne jamais laisser ensemble et sans surveillance le loup et la chèvre, ainsi que la chèvre et le chou fleur ?
On va construire un graphe dont les sommets sont les états possibles du système. A priori, le loup (L), la chèvre (C) et le chou fleur (F) peuvent être soit sur la rive gauche (G), soit sur la rive droite (D), soit sur le bateau (B).
- Sans tenir compte des contraintes sémantiques et numériques, combien de sommets aurait-on ? Construire la liste de tous ces sommets.
- Enlever les sommets tels qu'il y a deux éléments sur la barque.
- Enlever les sommets tels que le loup est avec la chèvre et ceux où la chèvre est avec le chou fleur.
- Ne pas oublier cependant que les trois éléments peuvent être simultanément sur la rive gauche ou sur la rive droite.
- Construire la fonction sont_lies(o,e) qui retourne True si et seulement si les sommets e et o peuvent être liés par une arête.
- Construire le graphe modélisant le problème.
- Demander à Networkx de construire le plus court chemin entre la situation initiale et la situation finale souhaitée. On utilisera pour cela la méthode shortest_path(G,source,target)
Récipients
On souhaite prélever 4 litres de liquide dans un tonneau. Pour cela, on dispose de deux récipients non gradués :
- l'un de 5 litres,
- l'autre de 3 litres.
Comment doit-on procéder ?
Résoudre le problème en faisant construire le graphe non orienté modélisant le problème et en demandant à Networkx de construire le plus court chemin entre la situation initiale et la situation finale attendue.
Lien vers Une solution possible.