WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Les graphes planaires
Graphe planaire
Définition
On rappelle la définition suivante...
Définition (Graphe planaire)
Un graphe est dit planaire s'il admet une représentation graphique dans le plan telle que deux arêtes quelconques ne se coupent pas.
Remarque : Rappelons que les arêtes ne sont pas forcément rectilignes.
Outre l'intérêt théorique (théorème des quatre couleurs, etc.), ou une représentation plus sympathique, chercher si un graphe possède une représentation planaire peut s'avérer pratiquement important. Par exemple, il était plus facile de concevoir les tout premiers circuits imprimés à transistors quand le graphe du circuit était planaire : on évitait alors de devoir recourir au procédé bicouche ou à des "straps" fragiles pour s'échapper du plan du circuit imprimé.
Notons qu'un graphe ne peut pas être planaire s'il possède un sous-graphe qui ne l'est pas : une fois dessiné dans un plan, un graphe planaire a forcément tous ses sous-graphes qui le sont aussi.
Exemples
Exemple : [$K_{3,3}$] Il est non planaire
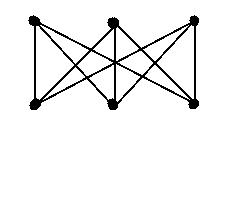
Exemple : [$K_n$] On rappelle que l'on note $K_n$ tout graphe non orienté simple d'ordre $n$, tel que toute paire de sommets est reliée par une unique arête. Alors $K_5$ n'est pas planaire :
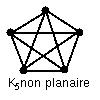
En dessinant $K_1$, $K_2$, $K_3$ et $K_4$, on constate qu'ils planaires. $K_5$, on l'a vu, ne l'est pas. Comme $K_5$ est un sous-graphe de $K_n, n \geqslant 5$, on en déduit qu'à partir de $n=5$, tous les $K_n$ ne sont plus planaires.
Caractérisation des graphes planaires
Pendant de nombreuses années, les mathématiciens ont tenté de caractériser les graphes planaires. Ce problème a été résolu en 1930 par le mathématicien polonais K. Kuratowski.
Expansion d'un graphe
Définition (Expansion d'un graphe)
L'expansion d'un graphe est le résultat de l'ajout d'un ou plusieurs sommets sur une ou plusieurs arêtes (par exemple, transformation de l'arête $\bullet - \bullet$ en $\bullet - \bullet - \bullet$).
On peut également définir l'opération inverse qui "simplifie" le graphe en contractant toutes les arêtes dont un des sommets a un degré 2. Par exemple, si un graphe expansé contient 3 sommets, A, B et C, que B est uniquement relié à A et C (donc de degré 2), alors on peut contracter, au choix, l'arête AB ou AC. Cela revient en pratique à supprimer AB, BC ainsi que B du graphe et de créer une arête AC.
Théorème de Kuratowski
La réponse au problème de caractérisation des graphes planaires est...
Théorème (Kuratowski)
Un graphe fini est planaire si et seulement s'il ne contient pas de sous-graphe qui soit une expansion de $K_5$ ou $K_{3,3}$.
Travaux pratiques
- Faire une fonction
get_Kn()qui construit et renvoie $K_n$, - Faire une fonction
get_K33()qui construit et renvoie $K_{3,3}$, - Faire des fonctions
is_K5(A)etis_K33(A)qui renvoie True si A est $K_5$, resp. $K_{3,3}$, - Faire une fonction
contract(A)qui contracte toutes les arêtes de A comportant un sommet de degré 2, - Faire une fonction
is_planar(A)qui renvoie True si A est planaire, et False sinon.
Remarque : vous aurez besoin des fonctions du TP2, notamment get_allsubgraph(A) qui renvoie tous les sous-graphe de A.
Dénombrement de régions
Le prochain problème classique que l'on présentera s'intéresse au nombre de régions qu'un graphe planaire découpe. La célèbre formule d'Euler permettra de relier ce nombre aux nombres d'arêtes et de sommets du graphe considéré.
Cartes, régions
Définition (Carte, régions)
Une carte est une représentation particulière d'un graphe planaire. On dit qu'une carte est connexe si son graphe l'est. Une carte divise le plan en plusieurs régions.
Exemple : Par exemple, la carte ci-dessous, avec six sommets et neuf arêtes, divise le plan en cinq régions (A, B, C, D, E).
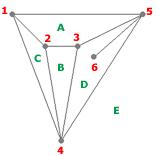
On remarque que quatre régions sont limitées alors que la cinquième (E), extérieure au diagramme, ne l'est pas.
Degré d'une région
Définition (Degré d'une région)
Le degré d'une région r, noté d(r), est la longueur du cycle ou de la chaîne fermée qui limite r.
Exemple : Dans le graphe ci-dessus, d(A)=4, d(B)=3, d(C)=3, d(D)=5, d(E)=3.
Remarque : On remarque que toute arête limite deux régions, ou est contenue dans une région et est alors comptée deux fois dans la chaîne fermée. Nous avons donc...
Lemme des régions
Théorème (Lemme des régions)
La somme des degrés des régions d'une carte connexe est égale à deux fois le nombre d'arêtes.
Exercice : Démontrez ce résulat.
Réponse : Il y a deux types d'arêtes, celles séparant deux régions données, et celles incluses à l'intérieur d'une région...
Formule d'Euler
Euler a établi une formule qui relie le nombre de sommets S, le nombre d'arêtes A et le nombre de régions R d'une carte connexe :
Théorème (Euler)
$S - A + R = 2$
Exercices
Exercice : Utilisez le résultat d'Euler pour retrouver le fait que $K_{3,3}$ n'est pas planaire.
Définition (Polyèdres réguliers, Solides de Platon)
Un polyèdre est dit régulier s'il est constitué de faces toutes identiques et régulières, et que tous ses sommets sont identiques. Ils sont au nombre de neuf, dont cinq seulement sont convexes. Ces derniers étaient connus de Platon :
- le tétraèdre régulier (4 faces en triangle équilatéral),
- le cube,
- l'octaèdre régulier (8 faces en triangle équilatéral),
- le dodécaèdre régulier (12 faces en pentagone),
- l'icosaèdre régulier (20 faces en triangle équilatéral).
Pour cette raison, ces cinq polyèdres réguliers convexes sont appelés Solides de Platon
Exercice : Les solides platoniciens peuvent être considérés comme des graphes, qui de plus sont planaires. Vérifier la formule d'Euler sur ces solides Platoniciens :
- le nombre de sommets,
- moins le nombre d'arêtes,
- plus le nombre de faces
...est toujours égal à 2.