---

Introduction

Dans ce TP, on va chercher à étudier quels sont les différents types de graphes que l'on peut obtenir à partir d'un graphe $G$, en lui enlevant soit des arêtes, soit des sommets.

Prenons l'exemple d'un ordinateur, avec imprimante, souris, etc. Chaque appareil est un sommet du graphe de l'installation informatique, et chaque câble est une arête. On peut alors, au choix, enlever des câbles électriques, ou des appareils (avec leurs câbles), pour obtenir ainsi une nouvelle installation informatique, c'est-à-dire construire un nouveau graphe à partir d'un graphe donné.

On considère, dans tout ce paragraphe, les graphes $G_1$ et $G_2$ suivants

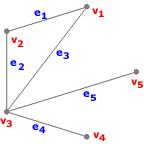
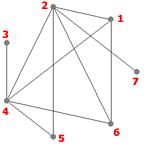
Ils nous serviront à illustrer les définitions à venir.

Graphe partiel et sous-graphe

Graphe partiel

---

Définition (Graphe partiel)

Soit G = (S, A) un graphe. Le graphe G' = (S, A') est un graphe partiel de G, si A' est inclus dans A.

---

Remarque : Autrement dit, on obtient G' en enlevant une ou plusieurs arêtes au graphe G (sans toucher à ses sommets).

---

Exemple : [Graphe partiel de $G_1$] Voici un exemple de graphe partiel de $G_1$

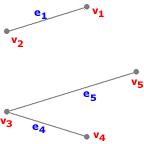
Ici,

• S'=S,
• A'={$e_1, e_4, e_5$}.

---

Sous-graphe

---

Définition (Sous-graphe)

On dit que le graphe $(S',A')$ est un sous-graphe du graphe $(S,A)$ si

1. $S' \subset S$,
2. $A' \subset A$,
3. $A'={(x,y)\mid (x,y) \in A \land x \in S' \land y \in S'}$

---

Remarque : Un sous-graphe d'un graphe donné est donc obtenu en enlevant certains sommets, et toutes les arêtes incidentes à ces sommets.

---

Exemple : [Sous-graphe de $G_1$] Voici un exemple de sous-graphe de $G_1$ :

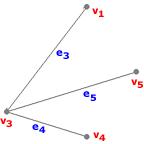
Ici,

• V'={$v_1, v_3, v_4, v_5$},
• E'={$e_3, e_4, e_5$}.

---

Travaux pratiques

1. Ecrire une fonction is_nodes_in(A,B) qui teste si les noeuds du graphe A sont inclus dans ceux du graphe B.
2. Ecrire une fonction is_edges_in(A,B) qui teste si les arêtes du graphe A sont incluses dans le graphe B.

Attention : les arêtes d'un graphe sont représentées par un couple (u,v) où u et v sont des sommets. Or, dans un graphe non orienté, l'ordre de u et v n'a pas d'importance et n'est pas forcément fixé par l'implentation de la classe Graph de netowrkx. Par conséquent, si on veut tester si une arête (u,v) de A se trouve dans B, il faut tester si (u,v) ou (v,u) se trouve dans B.

1. Ecrire une fonction is_partialgraph(A,B) qui teste si un graphe donné est un graphe partiel d'un autre graphe. On remarquera que:
   • G.nodes() renvoie la liste des noeuds de G,
   • G.edges() fait de même pour les arêtes,
   • Il suffit donc de regarder :
     • si les arêtes de A sont des arêtes de B (inclusion)
     • les sommets de A sont les sommets de B (égalité)
2. Faire de même une fonction is_subgraph(A,B) pour les sous-graphes
   • Il faut que :
     • Les sommets de A sont des sommets de B (inclusion)
     • Les arêtes de A sont des arêtes de B (inculsion)
     • Les arêtes de B constituées de sommets de A sont des arêtes de A

Remarque : comme pour la fonction is_edges_in(), il faut faire attention aux deux possibilités d'écrire une arête entre deux sommets u et v, à savoir (u,v) ou (v,u)

1. Faire des fonctions get_allpartialgraph(A) et get_allsubgraph(A) retournant tous les graphes partiels et tous les sous-graphes d'un graphe A donné
   • On pourra utiliser la fonction combination du module itertools, pour obtenir toutes les combinaisons possibles de sommets (et/ou d'arêtes).
2. Appliquer ces fonctions sur les graphes $G_1$ et $G_2$.

Sous-graphes particuliers

Sous-graphe partiel

---

Définition (Sous-graphe partiel)

Un graphe partiel d'un sous-graphe est un sous-graphe partiel de G.

---

Remarque : Cette fois-ci, on enlève des sommets (et leurs arêtes incidentes), puis des arêtes.

---

Exemple : [Sous-graphe partiel de $G_1$] Voici un sous-graphe partiel de $G_1$ :

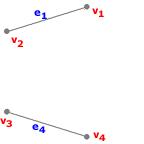
Ici,

• V'={$v_1, v_2, v_3, v_4$},
• E'={$e_1, e_4$}.

---

Clique

---

Définition (Clique)

On appelle clique un sous-graphe complet de G.

---

Remarque : On a donc réussi, en enlevant des sommets, à faire en sorte que chaque sommet est adjacent à tous les autres sommets.

---

Exemple : [Une clique de $G_1$] Exemple de clique de $G_1$ :

Ici,

• V'={$v_1,v_2,v_3$},
• E'={$e_1, e_2, e_3$}.

---

Stable

---

Définition (Stable)

On appelle stable un sous-graphe de $G$ sans arêtes.

---

Remarque : On enlève donc des sommets, et leurs arêtes adjacentes. On obtient un stable que si, en ayant enlevé un certain nombre de sommets à $G$, le sous-graphe résultant ne possède plus d'arête.

---

Exemple : [Un stable de $G_1$] Voici un stable de $G_1$ :

Ici,

• V'={$v_1, v_4, v_5$},
• E'={}.

---

Travaux pratiques

fonctions outils

1. Faire des fonctions recevant deux graphes en argument, et disant si le premier est un sous-graphe partiel (resp. une clique, un stable) du second.
2. Faire des fonctions produisant tous les sous-graphes partiels (resp. toutes les cliques, tous les stables) d'un graphe fourni en paramètre.
3. Trouver les sous-graphes partiels, les cliques et les stables pour $G_1$ et $G_2$.
4. Faire de même avec le graphe $G$ suivant :

exercice applicatif

Dans un groupe de six personnes, il y en :

• soit au moins trois qui se connaissent mutuellement,
• soit au moins trois qui ne se connaissent pas.

Cela revient à dire que, quel que soit le graphe $G$ à six sommets, si on génère tous ses sous-graphes de 3 sommets, alors il en existe forcément au moins un qui est :

• soit une clique (les trois sommets sont adjacents deux à deux),
• soit un stable (aucun arc).

Rq : cela n'est plus valable pour les graphes à cinq sommets.

L'exercice consiste à prouver cette proposition grâce à un programme, en utilisant notamment les fonctions créées précédemment.

D'autres travaux pratiques

Un premier exercice

Trouver les cliques du graphe G2 et donner les maximales :

Bibliothèque (d'après Didier Müller)

Sept étudiants, désignés par A, B, C, D, E, F et G, se sont rendus à la bibliothèque aujourd'hui. Le tableau suivant précise "qui a rencontré qui" (la bibliothèque étant petite, deux étudiants présents au même moment se rencontrent nécessairement $\ldots$).

Etudiant	A	B	C	D	E	F	G
a rencontré	D,E	D,E,F,G	E,G	A,B,E	A,B,C,D,F,G	B,E,G	B,C,E,F

• De combien de places assises dispose au minimum la bibliothèque sachant que chacun a pu travailler assis pendant sa (ou ses) période(s) de présence ?
• Qui était sur ces chaises au moment où la bibliothèque était la plus occupée ?

Incompatibilité (d'après Didier Müller)

On veut transporter des produits chimiques par le rail. A, B, C, D, E, F, G et H désignent huit produits chimiques. Dans le tableau ci-dessous, une croix signifie que les produits ne peuvent pas être entreposés dans le même wagon, car il y aurait risque d’explosion :

	A	B	C	D	E	F	G	H
A		x	x	x			x	x
B	x				x	x	x
C	x			x		x	x	x
D	x		x		x			x
E		x		x		x	x
F		x	x		x
G	x	x	x		x
H	x		x	x

• Quel nombre minimum de wagons faut-il ?
• Quelle est la répartition de ces produits dans les wagons ?