WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
La méthode PERT
Présentation de la méthode
Le problème du plus long chemin dans les digraphes sans circuits trouve une application dans l'ordonnancement et la planification des tâches composant un projet complexe, par exemple la construction d'une maison.
On fait correspondre à chaque tâche un arc d'un digraphe, sa durée d'exécution étant égale au poids de cet arc.
Le digraphe reflète les précédences requises dans l'exécution du projet. Ainsi, la tâche correspondant à l'arc $(i, j)$ ne peut commencer que si toutes les tâches correspondant à des arcs $(k, i)$ ont été complétées. Le digraphe peut contenir des tâches fictives de durée nulle afin de forcer certaines précédences.
Les sommets du digraphe représentent des événements, début (fin) des activités correspondant aux arcs dont ils sont l'extrémité initiale (finale). Le fait que le digraphe est sans circuit est garant de la faisabilité du projet. En effet, l'existence d'un circuit impliquerait une contradiction dans les précédences : une tâche devant en même temps précéder et succéder une autre!
On supposera dorénavant que les sommets ont déjà été numérotés de 1 à $n$ de manière compatible avec leurs rangs, c'est-à-dire que $r(j)>r(i)$ implique $j>i$ (voir l'algorithme de calcul du rang).
En plus, si le digraphe possède plusieurs sommets sans prédécesseurs, on supposera avoir introduit un sommet 1 relié par un arc de durée nulle à chacun de ces sommets. Ce sommet indique le début du projet.
De même, si le digraphe possède plusieurs sommets sans successeurs, ceux-ci seront reliés par un arc de durée nulle à un dernier sommet $n$ (fin du projet).
Enfin, on supposera éliminés les arcs parallèles par l'introduction de tâches fictives.
Algorithme du chemin critique
- Données
- Digraphe $G = (V, E)$, sans circuits, des activités avec leur durée $d_{ik}$.
- Résultat
- $d_i$ début au plus tôt des activités correspondant aux arcs $(i, k)$ partant de $i$,
- $j_i$ fin au plus tard des activités correspondant aux arcs $(k, i)$ arrivant à $i$,
- durée du chemin critique.
- Début
- Calcul des dates de début au plus tôt (récurrence en avançant dans le projet)
- $d_1 = 0$
- Pour $k = 2$ à $n$ faire $d_k = max{d_j + d_{jk} | j \in P(k)}$
- Calcul des dates de fin au plus tard (récurrence en reculant dans le projet)
- $j_n = d_n$
- Pour $k = n-1$ à 1 faire $j_k = min{j_j - d_{kj} | j \in S(k)}$
- Fin.
Notation: $P(i) = {k \in V | (k, i) \in E}$ est l'ensemble des sommets prédécesseurs de $i$.
Notation: $S(i) = {k \in V | (i, k) \in E}$ est l'ensemble des sommets successeurs de $i$.
Définitions
Définition (Sommet critique)
Un sommet $i$ est critique si $d_i = j_i$.
Définition (Arc critique)
Un arc $(i, j)$ est critique si ses extrémités sont des sommets critiques et $d_{ij} = d_j - d_i$.
Définition (Chemin critique)
Un chemin critique est un chemin de 1 à $n$ n'utilisant que des arcs critiques, c'est-à-dire des activités telles que tout retard dans leur exécution provoquerait un retard de la fin du projet.
Définition (Durée du chemin critique)
La durée du chemin critique est donnée par $d_n$ (ou par $j_n$, les deux valeurs étant toujours égales). Elle correspond à la durée minimale du projet étant données les durées des tâches le composant et les précédences respectives.
Exemple
Ci-dessous le graphe des précédences obtenu avec l'algorithme du chemin critique. Les sommets et les arcs critiques sont en rouge.
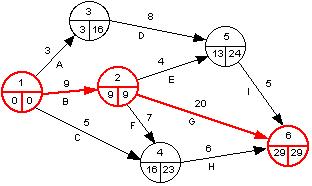
| $Tâches $ | $ Précédences $ | $ Durée [jours] $ |
| $A $ | $ - $ | $ 3 $ |
| $B $ | $ - $ | $ 9 $ |
| $C $ | $ - $ | $ 5$ |
| $D $ | $ A $ | $ 8 $ |
| $E $ | $ B $ | $ 4 $ |
| $F $ | $ B $ | $ 7$ |
| $G $ | $ B $ | $ 20$ |
| $H $ | $ C, F $ | $ 6$ |
| $I $ | $ D, E $ | $ 5$ |
Travaux pratiques
- Programmer la méthode PERT
- Résoudre l'exercice suivant
Exercice : La rénovation du séjour d'un appartement se décompose en plusieurs tâches décrites dans le tableau ci-dessous. Ce dernier donne également les précédences à respecter lors de la planification des travaux ainsi qu'une estimation de la durée de chacune des tâches.
| $ | Tâches | Précédences | Durée [jours] |
| $A $ | Enlèvement des portes | $ - $ | $ 1/2$ |
| $B $ | Ponçage et peinture des portes | $ A $ | $ 3 $ |
| $C $ | Pose des portes | $ B, J $ | $ 1/2 $ |
| $D $ | Arrachage des papiers peints | $ - $ | $ 1$ |
| $E $ | Tirage des fils électriques | $ D $ | $ 1 $ |
| $F $ | Pose des prises | $ E, H, I $ | $ 1/2 $ |
| $G $ | Ragréage des murs | $ E, A $ | $ 2$ |
| $H $ | Peinture du plafond | $ G $ | $ 2$ |
| $I $ | Pose des papiers peints | $ G $ | $ 3$ |
| $J $ | Peinture des cadres | $ H, I $ | $ 1$ |
| $K $ | Arrachage de la moquette | $ H, I, J $ | $ 1/2 $ |
| $L $ | Ponçage du parquet | $ K $ | $ 1$ |
| $M $ | Imprégnation et séchage du parquet | $ L, F $ | $ 4$ |
| $N $ | Peinture du balcon | $ - $ | $ 2$ |
| $O $ | Changement des protections solaires | $ N $ | $ 1$ |
- Représentez le graphe des précédences de ces travaux de rénovation.
- Déterminez une durée totale minimale de rénovation en exhibant un chemin critique dans le graphe précédent.