Présentation

Publié en 1959, l'algorithme de Edgser Wybe Dijkstra (1930-2002) est une alternative à Floyd, plus complexe mais plus rapide.

Ici, on se fixe un sommet source, et l'algorithme retourne tous les chemins les plus courts de ce sommet à chacun des autres sommets (légèrement différent du retour de Floyd)

Description de l'algorithme

Le principe

L'algorithme de Dijkstra est un algorithme de type glouton : à chaque nouvelle étape, on traite un nouveau sommet. Reste à définir le choix du sommet à traiter, et le traitement à lui infliger...

Tout au long du calcul, on met à jour deux ensembles :

$C$

Ensemble des sommets restant à visiter (au départ $C=S \setminus \{source\}$).

$D$

Ensemble des sommets pour lesquels on connaît déjà leur plus petite distance à la source (au départ, $D=\{source\})$.

L'algorithme se termine quand $C$ est vide.

Pour chaque sommet $s$ dans $D$, on conservera :

• dans un tableau distances, le poids du plus court chemin jusqu'à la source,
• dans un tableau parcours, le sommet $p$ qui le précède dans un plus court chemin de la source à $s$.

Ainsi, pour retrouver un chemin le plus court, il suffira de remonter de prédécesseur en prédécesseur jusqu'à la source, ce qui pourra se faire grâce à un unique appel récursif (beaucoup moins coûteux que dans le cas de Floyd).

Initialisation

Au début de l'algorithme, le chemin le plus court connu entre la source et chacun des sommets est le chemin direct, avec une arête de poids infini s'il n'y a pas de liaison entre les deux sommets.

On initialise donc le tableau distances par les poids des arêtes reliant la source à chacun des sommets, et le tableau parcours par source pour tous les sommets.

i^ème étape

On suppose avoir déjà traité i sommets, parcours et distances contiennent respectivement les poids et le prédécesseur des plus courts chemins pour chacun des sommets déjà traités.

Soit s le sommet de C réalisant le minimum de distances[s].

• On supprime s de C et on l'ajoute à D.
• Reste à mettre à jour les tableaux distances et parcours pour les sommets t reliés directement à s par une arête, comme suit... Si

distances[s] + F(s,t) < distances[t],

alors on remplace :

• distances[t] par distances[s] + F(s,t),
• parcours[t] par s.

Et c'est tout !

(n-2)^ème étape

Au départ, il y a (n-1) sommets à visiter, mais la dernière étape est inutile (elle n'apporte rien). Dès la (n-2)^ème étape, distances et parcours contiennent toute l'information nécessaire pour trouver des plus courts chemins.

Evaluation

Si $n$ est le nombre de sommets du graphe, et $a$ son nombre d'arêtes, alors l'algorithme de Dijkstra renvoie le résultat au bout de $O(a^2 ln n)$ opérations.

Pour un même résultat, Floyd nécessite $O(n^3)$ opérations.

Utilisation

Le protocole open shortest path first, qui permet un routage internet très efficace des informations, utilise Dijkstra.

Le réseau Internet utilise pour le moment un autre type d'algorithme pour déterminer le chemin à suivre pour transmettre des données entre deux serveurs : Routing Information Protocol (RIP). Dijkstra commence cependant à s'implanter, et remplace progressivement ce protocole : il est le plus rapide.

Les sites d'itinéraires routiers l'utilisent de la même manière et permettent de nombreuses adaptations en ajustant le poids des arcs (trajet le plus économique, le plus rapide, etc.)

Dijkstra en détail

L'algorithme

Numérotons les sommets du graphe $G = (V,E)$ de $1$ à $n$.

Supposons que l'on s'intéresse aux chemins partant du sommet 1.

On construit un vecteur $l = (l(1); l(2); ...; l(n))$ ayant $n$ composantes tel que $l(j)$ soit égal à la longueur du plus court chemin allant de 1 au sommet j.

On initialise ce vecteur à $c_{1,j}$, c'est-à-dire à la première ligne de la matrice des coûts du graphe, définie comme indiqué ci-dessous :

• 0 si i=j
• $+\infty$ (ou un grand nombre) si $i \neq j$ et $(i,j) \notin E$
• $\delta (i,j)$ si $i \neq j$ et $(i,j) \in E$.

où $\delta (i,j)$ est le poids (la longueur) de l'arc $(i,j)$. Les $c_{i,j}$ doivent être strictement positifs.

On construit un autre vecteur $p$ pour mémoriser le chemin pour aller du sommet 1 au sommet voulu. La valeur $p(i)$ donne le sommet qui précède $i$ dans le chemin.

On considère ensuite deux ensembles de sommets, $S$ initialisé à ${1}$ et $T$ initialisé à ${2, 3, ..., n}$.

À chaque pas de l'algorithme, on ajoute à $S$ un sommet jusqu'à ce que $S = V$ de telle sorte que le vecteur $l$ donne à chaque étape le coût minimal des chemins de 1 aux sommets de $S$.

Détails de l'algorithme de Dijkstra

On suppose ici que le sommet de départ (qui sera la racine de l'arborescence) est le sommet 1. Notons qu'on peut toujours renuméroter les sommets pour que ce soit le cas.

Initialisations

• $l(j) = c_{1,j}$ et $p(j) = NIL$, pour $1\leqslant j \leqslant n$
• Pour $2 \leqslant j \leqslant n$ faire Si $c_{1,j} < +\infty$ alors $p(j) = 1$.
• $S = {1}$ ; $T = {2, 3, ..., n}$.

Itérations

Tant que $T$ n'est pas vide faire

• Choisir $i$ dans $T$ tel que $l(i)$ est minimum
• Retirer $i$ de $T$ et l'ajouter à $S$
• Pour chaque successeur $j$ de $i$, avec $j$ dans $T$, faire Si $l(j) > l(i) + d(i,j)$ alors
  • $l(j) = l(i) + d(i,j)$
  • $p(j) = i$

Exemple

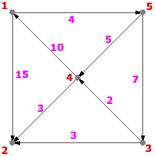
Initialisations

• $S = {1}$ ;
• $T = {2, 3, 4, 5}$ ;
• $l = (0, 15, \infty, \infty, 4)$;
• $p = (NIL, 1, NIL, NIL, 1)$.

Première itération

• $i = 5$ car $l(5) = min(15, \infty, \infty, 4) = 4$;
• $S = {1, 5}$; $T = {2, 3, 4}$;
• les successeurs de 5 dans $T$ sont 3 et 4;
• $l(3)$ prend la nouvelle valeur $min(\infty; l(5) + d(5; 3)) = min(\infty; 4 + 7) = 11$; $p(3) = 5$;
• $l(4)$ prend la nouvelle valeur $min(\infty ; l(5) + d(5; 4)) = 9$ ; $p(4) = 5$;
• d'où les nouveaux vecteurs $l = (0, 15, 11, 9, 4)$ et p = $(NIL, 1, 5, 5, 1)$

Deuxième itération

• $i = 4$; $l(4) = 9$;
• $S = {1, 5, 4}$; $T = {2, 3}$;
• le seul successeur de 4 dans $T$ est 2;
• $l(2)$ prend la nouvelle valeur $min(\infty; l(4) + d(4; 2)) = min(15; 9 + 3) = 12$; $p(2) = 4$;
• d'où les nouveaux vecteurs $l = (0, 12, 11, 9, 4)$ et $p = (NIL, 4, 5, 5, 1)$

Troisième itération

• $i = 3$; $l(3) = 11$;
• $S = {1, 5, 4, 3}$; $T = {2}$;
• le seul successeur de 3 dans $T$ est 2;
• $l(2)$ garde sa valeur car $min(12; l(3) + d(3; 2)) = min(12; 11 + 3) = 12$;
• d'où les vecteurs inchangés $l = (0, 12, 11, 9, 4)$ et $p = (NIL, 4, 5, 5, 1)$

Quatrième itération

• $i = 2$; $l(2) = 12$;
• $S = {1, 5, 4, 3, 2}$; $T={}$; FIN.
• $l = (0, 12, 11, 9, 4)$;
• $p = (NIL, 4, 5, 5, 1)$.

Le chemin minimal de 1 à 4 par exemple est de coût 9. C'est le chemin 1-5-4, car $p(4) = 5$ et $p(5) = 1$.

Travaux pratiques

1. Reprogrammez cet algorithmes, en utilisant la structure de graphe propre à networkx.
2. L'appliquer aux deux exemples précédents, en comparant le temps d'exécution avec l'algorithme de networkx (on pourra se renseigner sur le module timeit).

Dijkstra et networkx

Montrons comment calculer le plus court chemin d'un graphe pondéré, et sa longueur (son temps), en utilisant la méthode de Dijkstra de networkx :

  >>> path.dijkstra_path(G,(0,0),(3,4))
  [(0, 0), (1, 0), (1, 1), (1, 2), (1, 3), (2, 3), (2, 4), (3, 4)]
  >>> path.dijkstra_path_length(G,(0,0),(3,4))
  38

Si la programmation de cet algorithme est un peu plus compliquée, son utilisation est plus simple.

Travaux pratiques

1. Utiliser networkx avec le graphe de l'exemple ci-dessus pour trouver tous les plus courts chemins en partant des sommets 2, 3, 4 et 5.
2. Comparer l'algorithme de Dijkstra de networkx au vôtre : vérifier qu'il fournit les mêmes plus court chemins, comparer le temps de calcul.