Introduction à Networkx

Le module Networkx est normalement installé en salle TP. Pour travailler chez vous, vous pouvez le télécharger ici. Il est aussi empaqueté dans la plupart des distributions GNU/Linux. Ainsi, pour l'installer proprement sous Debian/Ubuntu :

  $ sudo apt-get install python-networkx

Exemple de base

Module permettant de manipuler des graphes. Pour l'importer :

  >>> from networkx import *

Puis, pour créer un graphe (non orienté) :

  >>> G=Graph()

Ajouter un ou plusieurs nœuds (node, en anglais) :

  >>> G.add_node(1)
  >>> G.add_nodes_from([2,3])

La seconde ligne ajoute des nœuds à partir d'une liste, quand la première ligne ajoute un seul nœud (au nom de 1). Pour ajouter des arcs (edge, en anglais) :

  >>> G.add_edges_from([(1,2),(1,3)])

Pour lister les nœuds ou les sommets d'un graphe :

  >>> G.nodes()
  >>> G.edges()

Obtenir une représentation graphique avec Pylab :

  >>> import pylab as P
  >>> draw(G)
  >>> P.show()
  >>> draw_circular(G)
  >>> P.show()

Cas des digraphes

Pour réaliser un digraphe (ou graphe orienté) avec networkx, et le visualiser avec Pylab, on utilise la classe DiGraph au lieu de Graph :

  >>> from networkx import *
  >>> G = DiGraph()
  >>> G.add_nodes_from([0,1,2,3,4])
  >>> G.add_edges_from([(0,1),(1,0),(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)])
  >>> draw(G)
  >>> import pylab as P
  >>> P.show()

Autres graphes

Liste des graphes

networks utilise 4 classes différentes, selon le type de graphe :

Graph()

Un graphe non orienté sans boucle, ni arc multiple.

DiGraph()

Un graphe orienté sans boucle, ni arc multiple.

MultiGraph()

Un graphe non orienté, pouvant avoir boucles et arcs multiples.

MultiDiGraph()

Un graphe orienté, pouvant avoir boucles et arcs multiples.

Exemple

Montrons comment créer un MultiDiGraph, avec boucles :

  >>> G = MultiDiGraph()
  >>> G.add_nodes_from([1,2,3,4])
  >>> G.add_edges_from([(1,1),(1,2),(1,3),(2,3),(3,3),(2,4),(4,4)])

On peut alors demander le nombre de boucles, et la liste des boucles :

  >>> G.number_of_selfloops()
  >>> G.selfloop_edges()

Dessiner K5

Mise en page : neato

Cette fois-ci, on n'utilise pas Pylab, pour représenter le graphe, mais graphviz (installé en salle de TP ?) :

  >>> from networkx import *
  >>> G=complete_graph(5) # K5 est le graphe complet à 5 noeuds
  >>> A=to_agraph(G)      # convertion vers graphviz 
  >>> A.layout()          # choix de la mise en page : celle de base (neato)
  >>> A.draw("k5.ps")     # écriture du résultat dans un fichier postscript

Le résultat doit être visualisé à part. Pour visualiser le fichier k5.ps, on peut par exemple taper ceci dans un terminal (sous linux) :

   $ evince k5.ps

Autres mises en pages

Au lieu d'utiliser la mise en page de base, à savoir neato, on peut en préciser une autre :

  >>> A=to_agraph(G)
  >>> A.layout(prog='dot')
  >>> A.draw('graphe2.jpg')

Les choix possibles sont : neato,dot,twopi,circo,fdp, et nop.

La documentation

Vous pourrez trouver d'autres informations, de la documentation et l'API sur le site de Networkx : ici.

Travaux pratiques

Un premier graphe non orienté

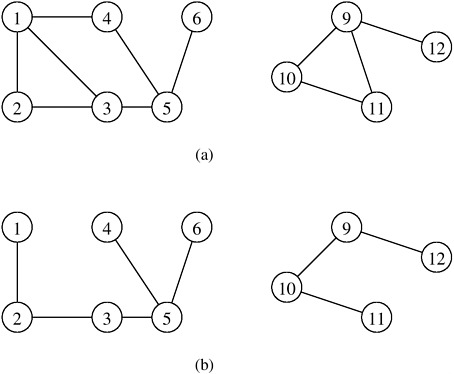
1. Coder les graphes ci-dessous (ils sont non orientés) ;
2. Afficher le degré de chacun des sommets, c'est-à-dire son nombre d'arêtes (G.degree(x) fournit le nombre d'arêtes du sommet x dans G) des graphes et afficher les degrés de ce dernier

Petit bout de code en guise d'exemple :

  >>> from networkx import *
  >>> G = Graph()
  >>> G.add_nodes_from([1,2,3,4])
  >>> G.add_edges_from([(1,2),(1,3),(1,4),(2,3)])
  >>> G.degree(1)
  3

Graphe régulier

En exploitant la méthode random_regular_graph(d, n), faire générer des graphes réguliers de $n$ sommets, chacun étant de degré $d$

1. degré 3 à 2 sommets,
2. degré 3 à 4 sommets,
3. degré 4 à 2 sommets.

Certains de ces graphes posent problème ? Pourquoi ?

Dot et graphviz

Présentation

Il existe un langage, du nom de dot, permettant de décrire les graphes afin de les représenter. Il fait partie du paquage graphviz évoqué ci-dessus (que vous pouvez aussi installer chez vous). Par exemple, pour réaliser le graphe orienté suivant

On peut saisir ce qui suit dans un fichier toto.dot...

  strict digraph  {
	1 -> 1 [label = "1/2"];
	1 -> 2 [label = "1/2"];
	2 -> 1 [label = "1/3"];
	2 -> 2 [label = "1/3"];
        2 -> 3 [label = "1/3"];
	3 -> 2 [label = "1/2"];
	3 -> 3 [label = "1/2"];
  }

et, dans un shell, transformer ce fichier texte en image :

  $ dot toto.dot -T png > toto.png

L'option -T permet de spécifier le type de fichier de sortie.

Enfin, pour visualiser ledit fichier :

  $ eog toto.png

dot n'est pas l'unique moteur de rendu de graphviz. Il y a aussi : neato, twopi, circo, fdp et nop.

Il suffit de remplacer, dans la ligne shell ci-dessus, dot par circo, par exemple, pour générer une représentation graphique différente.

Travaux pratiques

• Réaliser une méthode to_dot(G), qui transforme G en sa description en langage dot et qui retourne le résultat
• Réaliser une méthode show(G) qui crée une image de G, en utilisant dot, et l'affiche à l'écran.

• Réaliser une méthode save(G,nom) qui sauvegarde le graphe G.
  • Si le nom de fichier a une extension .dot, on sauvegardera le retour de to_dot() dans un fichier texte.
  • Si cette extension est .png, on sauvegardera l'image du graphe, créée grâce à dot.

Exercice d'entraînement

Michel est invité par André à un dîner de famille. Dès son arrivée, il se présente à chacune des onze autres personnes qu'il trouve dans la maison. Les onze premières phrases qu'il entend successivement sont les suivantes :

• Béatrice : "Bonjour ! Je suis la mère d'André."
• Carole : "Bienvenue ! Je suis la sœur du père d'André."
• Daniel : "Salut ! Je suis le fils unique de la sœur de la mère d'André."
• Émile : "Bonjour ! Je suis l'unique beau-frère du fils de Karl."
• Fabienne : "Mère de deux filles, je suis aussi la grand-mère maternelle de Daniel."
• Gaston : "Salut ! Je suis un des fils de Lucien et un des petits-fils de Fabienne."
• Honoré : "Je suis le grand-père paternel de Lucien."
• Irène : "Je suis l'unique belle-sœur de Lucien."
• Joseph : "Salut ! Je suis le neveu de Lucien et le petit fils de Karl."
• Karl: Mon petit-fils m'a parlé de vous.
• Lucien : Bienvenue dans ma maison, je vous ai vu a l'instant parler avec mon père.

Et la famille d'ajouter d'une seule voix : "si vous ne trouvez pas les liens familiaux qui nous unissent, vous n'aurez pas à dîner !"

Rq : dans cet exercice, le beau-frère de X est le frère du mari/femme de X, et la belle-soeur la soeur du mari/femme de X.

1. Représenter la situation familiale de ses hôtes au moyen d'un graphe.
2. Le coder ensuite dans NetworkX.
3. L'afficher à l'écran.

(d'après F. Droesbeke, les graphes par l'exemple, ellipse)