WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Problemes De Graphes
Dans ce chapitre, différents problèmes classiques autour des graphes seront présentés. On verra successivement les problèmes suivants, et on en proposera des solutions :
- Existence d'un circuit eulérien.
- Caractérisation des graphes extraits d'un graphe donné.
- Caractérisation des graphes planaires.
- Dénombrement des régions induites par un graphe planaire.
- Existence d'un circuit hamiltonien.
Circuits eulériens
Introduction : les ponts de Königsberg
La question à l'origine de la théorie des graphes est due à Euler, en 1736 : dans cette partie de la ville de Königsberg :
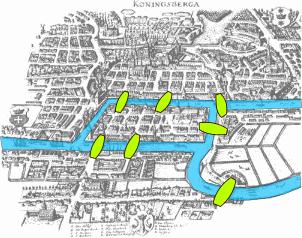
Peut-on, lors d'une promenade, revenir à notre point de départ en empruntant une, et une seule fois, chaque pont ?
Pour y répondre, Euler a introduit le graphe suivant (les arcs symbolisent les ponts ; les sommets, les quatre zones terrestres) :

Le problème de départ se ramène alors à la question suivante : peut-on trouver un circuit permettant d'emprunter une, et une seule fois chaque arête, en retournant à son point de départ ?
La réponse, dans ce cas particulier, est non : comme
- le point de départ $s$ est aussi le point d'arrivée,
- on ne peut pas emprunter deux fois une même arête,
on en conclut forcément que le degré de $s$ est pair. Or, dans le graphe ci-dessus, tous les sommets ont un degré impair.
Définitions
Ce problème, introduit par Euler, conduit aux définitions suivantes...
Définition (Chaîne eulérien)
On appelle chaîne eulérienne une chaîne contenant une et une seule fois toutes les arêtes du graphe.
Définition (Circuit eulérien)
On appelle circuit eulérien un circuit contenant une et une seule fois toutes les arêtes du graphe.
Remarque : On n'a plus affaire à une chaîne, mais à un circuit : le point de départ et celui d'arrivée coïncident.
Définition (Graphe eulérien)
Un graphe eulérien est un graphe possédant un circuit eulérien.
Remarque : On peut passer plusieurs fois par un sommet donné, pourvu que les arêtes empruntées soient toutes différentes.
Exercice : Donnez des exemples de graphes possèdant des circuits eulériens, et d'autres exemples de graphes n'en possédant pas.
Résultat d'Euler
Du problème initial d'Euler, on peut en déduire le résultat suivant (rappelons qu'il s'agit ici de graphes non orientés)...
Théorème
Il y a équivalence entre :
- posséder une chaîne eulérienne,
- être connexe, avec O ou 2 sommets de degré impair.
De plus, s'il n'y a pas de sommet de degré impair, alors le graphe est Eulérien.
Preuve : En parcourant un chemin ou un circuit, pour chaque sommet visité, on utilise une arête pour arriver à ce sommet et une arête pour en repartir, ces deux arêtes ne devant plus être utilisées par la suite.
Le nombre d'arêtes utilisables en ce sommet diminue donc de deux. Si un sommet est d'ordre impair, une de ses arêtes aboutissant à ce sommet doit donc être soit sur la première arête d'un chemin, soit sur la dernière.
Un chemin n'ayant que deux extrémités, le nombre de sommets d'ordre impair ne peut excéder deux.
Exercice : Soit G un graphe connexe non eulérien. Est-il toujours possible de rendre G eulérien en lui rajoutant un sommet et quelques arêtes?
Réponse : Oui. Quand on ajoute un nouveau sommet, son nombre d'arêtes doit être pair, pour ne pas poser de nouveaux problèmes. On peut donc ainsi corriger le problème d'imparité pour un nombre pair de sommets : en reliant chaque couple de deux sommets de degré impairs, à un sommet que l'on crée uniquement pour ce couple. Or, tout graphe simple possède un nombre pair de sommets de degré impair...
Exercice : les dominos
Exercice : On considère des dominos dont les faces sont numérotées 1, 2, 3, 4 ou 5.
- En excluant les dominos doubles, de combien de dominos dispose-t-on ?
- Montrez que l'on peut arranger ces dominos de façon à former une boucle fermée (en utilisant la règle habituelle de contact entre les dominos).
- Pourquoi n'est-il pas nécessaire de considérer les dominos doubles ?
- Si l'on prend maintenant des dominos dont les faces sont numérotées de 1 à n, est-il possible de les arranger de façon à former une boucle fermée ?
Réponse :
- On dispose de 4+3+2+1 = 10 dominos.
- Considérons $K_5$, le pentagramme complet. A l'arête $(1,2)$, par exemple, est associée le domino $(1,2)$. Arriver à constituer une boucle fermée de dominos revient donc à trouver un circuit eulérien dans $K_5$. C'est possible : $K_5$ est connexe, avec tous ses sommets de degré pairs.
- Considérer les dominos doubles revient à placer une boucle à chaque sommet de $K_5$. On ne change pas sa connexité, ni la parité de ses sommets.
- On obtient, dans ce cas, $K_n$, dont chaque sommet a pour degré $n-1$. Pour arriver à consitituer une boucle fermée, il faut donc (et il suffit) que $n$ soit impair.
Graphes partiels et sous-graphes
Introduction
Dans cette section, on va chercher à étudier quels sont les différents types de graphes que l'on peut obtenir à partir d'un graphe $G$, en lui enlevant soit des arêtes, soit des sommets.
Prenons l'exemple d'un ordinateur, avec imprimante, souris, etc. Chaque appareil est un sommet du graphe de l'installation informatique, et chaque câble est une arête. On peut alors, au choix, enlever des câbles électriques, ou des appareils (avec leurs câbles), pour obtenir ainsi une nouvelle installation informatique, c'est-à-dire construire un nouveau graphe à partir d'un graphe donné.
On considère, dans tout ce paragraphe, les graphes $G_1$ et $G_2$ suivants
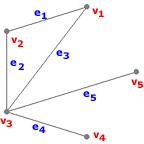
Ils nous serviront à illustrer les définitions à venir.
Graphe partiel et sous-graphe
Graphe partiel
Définition (Graphe partiel)
Soit G = (S, A) un graphe. Le graphe G' = (S, A') est un graphe partiel de G, si A' est inclus dans A.
Remarque : Autrement dit, on obtient G' en enlevant une ou plusieurs arêtes au graphe G (sans toucher à ses sommets).
Exemple : [Graphe partiel de $G_1$] Voici un exemple de graphe partiel de $G_1$
Ici,
- S'=S,
- A'={$e_3, e_4, e_5$}.
Exercice : Trouver un graphe partiel de $G_2$.
Sous-graphe
Définition (Sous-graphe)
On dit que le graphe $(S',A')$ est un sous{-graphe} du graphe $(S,A)$ si
- $S' \subset S$,
- $A' \subset A$,
- $A'={(x,y)\mid (x,y) \in A \land x \in S' \land y \in S'}$
Remarque : Un sous{}-graphe d'un graphe donné est donc obtenu en enlevant certains sommets, et toutes les arêtes incidentes à ces sommets.
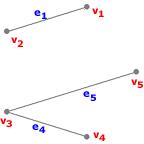
Exemple : [Sous-graphe de $G_1$] Voici un exemple de sous-graphe de $G_1$ :
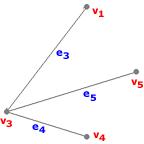
Ici,
- V'={$v_1, v_3, v_4, v_5$},
- E'={$e_3, e_4, e_5$}.
Exercice : Trouver un sous-graphe de $G_2$.
Exercice : Combien un graphe $G$ d'ordre $n$ possède-t-il de sous-graphes ?
Réponse : $2^n-1$, si l'on ne compte pas $G$.
Sous-graphes particuliers
Sous-graphe partiel
Définition (Sous-graphe partiel)
Un graphe partiel d'un sous-graphe est un sous-graphe partiel de G.
Remarque : Cette fois-ci, on enlève des sommets (et leurs arêtes incidentes), puis des arêtes.
Exemple : [Sous-graphe partiel de $G_1$] Voici un sous-graphe partiel de $G_1$ :
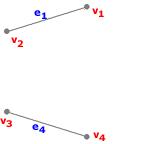
Ici,
- V'={$v_1, v_2, v_3, v_4$},
- E'={$e_1, e_4$}.
Exercice : Trouver un sous-graphe partiel de $G_2$.
Clique
Définition (Clique)
On appelle clique un sous-graphe complet de G.
Remarque : On a donc réussi, en enlevant des sommets, à faire en sorte que chaque sommet est adjacent à tous les autres sommets.
Exemple : [Une clique de $G_1$] Exemple de clique de $G_1$ :

Ici,
- V'={$v_1,v_2,v_3$},
- E'={$e_1, e_2, e_3$}.
Exercice : Trouver une clique de $G_2$.
Stable
Définition (Stable)
On appelle stable un sous-graphe de $G$ sans arêtes.
Remarque : On enlève donc des sommets, et leurs arêtes adjacentes. On obtient un stable que si, en ayant enlevé un certain nombre de sommets à $G$, le sous-graphe résultant ne possède plus d'arête.
Exemple : [Un stable de $G_1$] Voici un stable de $G_1$ :

Ici,
- V'={$v_1, v_4, v_5$},
- E'={}.
Exercice : Trouver un stable de $G_2$.
Exercices
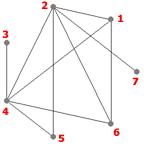
Exercice : On considère le graphe $G$ suivant :

En extraire : un graphe partiel, un sous-graphe, un sous-graphe partiel, une clique et un stable.
Exercice : Montrez que dans un groupe de six personnes, il y en a nécessairement trois qui se connaissent mutuellement ou trois qui ne se connaissent pas (on suppose que si A connaît B, B connaît également A).
Montrez que cela n'est plus nécessairement vrai dans un groupe de cinq personnes.
Réponse : Cela revient à dire que, dans un graphe $G$ à six sommets, il est toujours possible d'obtenir un sous-graphe (i.e., en enlevant trois sommets), qui est :
- soit une clique (les trois sommets sont adjacents deux à deux),
- soit un stable (aucun arc).
Cela n'est plus valable pour les graphes à cinq sommets.
Graphe planaire
Définition
On rappelle la définition suivante...
Définition (Graphe planaire)
Un graphe est dit planaire s'il admet une représentation graphique dans le plan telle que deux arêtes quelconques ne se coupent pas.
Remarque : Rappelons que les arêtes ne sont pas forcément rectilignes.
Outre l'intérêt théorique (théorème des quatre couleurs, etc.), ou une représentation plus sympathique, chercher si un graphe possède une représentation planaire peut s'avérer pratiquement important. Par exemple, il était plus facile de concevoir les tout premiers circuits imprimés à transistors quand le graphe du circuit était planaire : on évitait alors de devoir recourir au procédé bicouche ou à des "straps" fragiles pour s'échapper du plan du circuit imprimé.
Exercice : Un graphe peut-il être planaire s'il possède un sous-graphe qui ne l'est pas ?
Réponse : Non : une fois dessiné dans un plan, un graphe planaire a forcément tous ses sous-graphes qui le sont aussi.
Exemples
Exemple : [$K_{3,3}$] Il est non planaire

Exemple : [$K_n$] On rappelle que l'on note $K_n$ tout graphe non orienté simple d'ordre $n$, tel que toute paire de sommets est reliée par une unique arête. Alors $K_5$ n'est pas planaire :
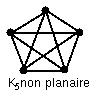
Exercice : Dessiner $K_1$, $K_2$, $K_3$ et $K_4$. Sont-ils planaires ? Et qu'en est-il de $K_n, n \geqslant 5$ ?
Réponse : $K_1$, $K_2$, $K_3$ et $K_4$ sont planaires. $K_5$, on l'a vu, ne l'est pas. Comme $K_5$ est un sous-graphe de $K_n, n \geqslant 5$, on en déduit qu'à partir de $n=5$, tous les $K_n$ ne sont plus planaires.
Caractérisation des graphes planaires
Pendant de nombreuses années, les mathématiciens ont tenté de caractériser les graphes planaires. Ce problème a été résolu en 1930 par le mathématicien polonais K. Kuratowski.
Expansion d'un graphe
Définition (Expansion d'un graphe)
L'expansion d'un graphe est le résultat de l'ajout d'un ou plusieurs sommets sur une ou plusieurs arêtes (par exemple, transformation de l'arête $\bullet - \bullet$ en $\bullet - \bullet - \bullet$).
Exercice : Représentez deux graphes, le second étant une expansion du premier.
Théorème de Kuratowski
La réponse au problème de caractérisation des graphes planaires est...
Théorème (Kuratowski)
Un graphe fini est planaire si et seulement s'il ne contient pas de sous-graphe qui est une expansion de $K_5$ ou $K_{3,3}$.
Exercice :
Dénombrement des régions d'un graphe planaire
Le prochain problème classique que l'on présentera s'intéresse au nombre de régions qu'un graphe planaire découpe. La célèbre formule d'Euler permettra de relier ce nombre aux nombres d'arêtes et de sommets du graphe considéré.
Cartes, régions
Définition (Carte, régions)
Une carte est une représentation particulière d'un graphe planaire. On dit qu'une carte est connexe si son graphe l'est. Une carte divise le plan en plusieurs régions.
Exemple : Par exemple, la carte ci-dessous, avec six sommets et neuf arêtes, divise le plan en cinq régions (A, B, C, D, E).
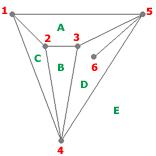
On remarque que quatre régions sont limitées alors que la cinquième (E), extérieure au diagramme, ne l'est pas.
Degré d'une région
Définition (Degré d'une région)
Le degré d'une région r, noté d(r), est la longueur du cycle ou de la chaîne fermée qui limite r.
Exemple : Dans le graphe ci-dessus, d(A)=4, d(B)=3, d(C)=3, d(D)=5, d(E)=3.
Remarque : On remarque que toute arête limite deux régions, ou est contenue dans une région et est alors comptée deux fois dans la chaîne fermée. Nous avons donc...
Lemme des régions
Théorème (Lemme des régions)
La somme des degrés des régions d'une carte connexe est égale à deux fois le nombre d'arêtes.
Exercice : Démontrez ce résulat.
Réponse : Il y a deux types d'arêtes, celles séparant deux régions données, et celles incluses à l'intérieur d'une région...
Formule d'Euler
Euler a établi une formule qui relie le nombre de sommets S, le nombre d'arêtes A et le nombre de régions R d'une carte connexe :
Théorème (Euler)
$S - A + R = 2$
Exercices
Exercice : Utilisez le résultat d'Euler pour retrouver le fait que $K_{3,3}$ n'est pas planaire.
Définition (Polyèdres réguliers, Solides de Platon)
Un polyèdre est dit régulier s'il est constitué de faces toutes identiques et régulières, et que tous ses sommets sont identiques. Ils sont au nombre de neuf, dont cinq seulement sont convexes. Ces derniers étaient connus de Platon :
- le tétraèdre régulier (4 faces en triangle équilatéral),
- le cube,
- l'octaèdre régulier (8 faces en triangle équilatéral),
- le dodécaèdre régulier (12 faces en pentagone),
- l'icosaèdre régulier (20 faces en triangle équilatéral).
Un graphe fini est planaire si et seulement s'il ne contient pas de sous-graphe qui est une expansion de K5 (la clique à 5 sommets) ou K3,3 (le graphe complet biparti à 3+3 sommets).
L'expansion d'un graphe est le résultat de l'ajout d'un ou plusieurs sommets sur une ou plusieurs arêtes (par exemple, transformation de l'arête •——• en •—•—•). Pour cette raison, ces cinq polyèdres réguliers convexes sont appelés Solides de Platon
Remarque : On appelle parfois polyèdres réguliers uniquement les 5 solides de Platon.
Exercice : Les solides platoniciens peuvent être considérés comme des graphes, qui de plus sont planaires. Vérifier la formule d'Euler sur ces solides Platoniciens :
- le nombre de sommets,
- moins le nombre d'arêtes,
- plus le nombre de faces
...est toujours égal à 2.
Circuit hamiltonien
Les dodécaèdres de Hamilton
Le dodécaèdre est à l'origine d'un autre problème célèbre, dû à Hamilton : comment passer une, et une seule fois, par chacun des sommets du dodécaèdre, de telle manière que le dernier sommet visité est aussi le premier.
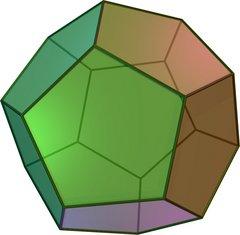
Définition
Définition (Circuit et graphes hamiltoniens)
Un circuit hamiltonien est un circuit qui passe par tous les sommets du graphe, une et une seule fois. Un graphe possédant un tel circuit est qualifié d'hamiltonien.
Remarque : C'est un circuit : le sommet de départ doit aussi être le sommet d'arrivée.
Exemple : Les graphes complets $K_n$ sont hamiltoniens, pour tout $n$.
Preuve : On peut inscrire $K_n$ dans un polygone régulier à $n$ sommets : il suffit alors de parcourir ce polygone, sommet par sommet, dans le sens trigonométrique par exemple, jusqu'à retrouver son point de départ.
Remarque : Dans le cas des graphes orientés (voir plus loin), on parle de graphe hamiltonien s'il est possible de trouver un cycle passant une et une seule fois par tous les sommets.
Remarque : Il peut y avoir plusieurs circuits hamiltoniens dans un graphe hamiltonien.
Le problème de la caractérisation des graphes Hamiltoniens n'est pas aussi simple que celui des graphes Eulériens. On peut cependant énoncer quelques conditions, respectivement nécessaires, puis suffisantes, pour qu'un graphe le soit...
Conditions nécessaires
Théorème
Un graphe hamiltonien d'ordre $n \geqslant 3$ ne possède pas de sommet de degré 1.
Preuve : Si un sommet $s$ est de degré 1, il est connecté à un (unique) autre sommet $s'$, qui sera forcément parcouru deux fois (pour aller en $s$, et pour en sortir).
Remarque : $K_2$ est hamiltonien, et a tous ses sommets d'ordre 1...
Théorème
Si un graphe hamiltonien possède un sommet de degré 2, alors les deux arêtes incidentes à ce sommet doivent faire partie du cycle hamiltonien.
Preuve : Supposons que $s$ est de degré 2, connecté à $s_1$ par l'arête $a_1$, et à $s_2$ par $a_2$. On est arrivé à $s$ à partir d'une arête, mettons $a_1$ ; si on réempruntait $a_1$ pour sortir de $s$, alors on repasserait par $a_1$, ce qui est impossible.
Conditions suffisantes
Théorème (Théorème de Ore)
Soit G = (V, E) un graphe simple d'ordre $n\geqslant 3$. Si pour toute paire {x,y} de sommets non adjacents, on a $d(x) + d(y) \geqslant n$, alors G est hamiltonien.
Théorème (Corollaire de Dirac)
Soit G = (V, E) un graphe simple d'ordre $n\geqslant 3$. Si pour tout sommet x de G, on a $d(x) \geqslant n/2$, alors G est hamiltonien.
Preuve : En effet, un tel graphe vérifie les conditions du théorème précédent. Si x et y ne sont pas adjacents, on a bien : $d(x) + d(y) \geqslant n/2 + n/2 = n$
Exercice : Dessinez un graphe d'ordre au moins 5 qui est...
- hamiltonien et eulérien,
- hamiltonien et non eulérien,
- non hamiltonien et eulérien,
- non hamiltonien et non eulérien.
Le problème du voyageur de commerce
Trouver un cycle hamiltonien pour un graphe donné est un problème difficile sur le plan algorithmique -- de type NP-complet --, relié au problème dit du voyageur de commerce : un voyageur de commerce doit visiter un ensemble de villes, en minimisant son temps de parcours.
Ce problème se formalise aisément en théorie des graphes :
- Les villes sont les sommets d'un graphe pondéré.
- Les arêtes correspondent aux routes reliant ces villes.
- La pondération correspond soit à la distance entre deux ville (en kilomètres), soit à la durée nécessaire pour passer d'une ville à l'autre.
- Ce graphe peut être orienté, si l'on souhaite intégrer des routes à sens unique.
On cherche alors à visiter tous les sommets du graphe (i.e. toutes les villes) en minimisant le « poids » du parcours (la distance parcourue, ou le temps total).
Le problème du voyageur de commerce correspond donc à la recherche d'un cycle hamiltonien de poids minimal, dans un graphe pondéré complet. Ce problème est NP-complet, donc impossible à résoudre exactement quand le nombre de villes est grand.