---

Algorithme de Dijkstra

Présentation

Edgser Wybe Dijkstra (1930-2002) a proposé en 1959 un algorithme qui permet de calculer le plus court chemin entre un sommet particulier et tous les autres.

Le résultat est une arborescence.

L'algorithme

Numérotons les sommets du graphe $G = (V,E)$ de $1$ à $n$.

Supposons que l'on s'intéresse aux chemins partant du sommet 1.

On construit un vecteur $l = (l(1); l(2); ...; l(n))$ ayant $n$ composantes tel que $l(j)$ soit égal à la longueur du plus court chemin allant de 1 au sommet j.

On initialise ce vecteur à $c_{1,j}$, c'est-à-dire à la première ligne de la matrice des coûts du graphe, définie comme indiqué ci-dessous :

$\left{\begin{array}{ll}0 & \textrm{ si } i=j \\+\infty & \textrm{ si } i \neq j \textrm{ et } (i,j) \notin E\\\delta (i,j) & \textrm{ si } i \neq j \textrm{ et } (i,j) \in E\\\end{array}\right.$

où $\delta (i,j)$ est le poids (la longueur) de l'arc $(i,j)$. Les $c_{i,j}$ doivent être strictement positifs.

On construit un autre vecteur $p$ pour mémoriser le chemin pour aller du sommet 1 au sommet voulu.

La valeur $p(i)$ donne le sommet qui précède $i$ dans le chemin.

On considère ensuite deux ensembles de sommets, $S$ initialisé à ${1}$ et $T$ initialisé à ${2, 3, ..., n}$.

À chaque pas de l'algorithme, on ajoute à $S$ un sommet jusqu'à ce que $S = V$ de telle sorte que le vecteur $l$ donne à chaque étape le coût minimal des chemins de 1 aux sommets de $S$.

Description de l'algorithme de Dijkstra

On suppose ici que le sommet de départ (qui sera la racine de l'arborescence) est le sommet 1. Notons qu'on peut toujours renuméroter les sommets pour que ce soit le cas.

Initialisations

• $l(j) = c1,j et p(j) = NIL, pour 1\leqslant j \leqslant n$
• Pour $2 \leqslant j \leqslant n$ faire Si $c_{1,j} < +\infty$ alors $p(j) = 1$.
• $S = {1}$ ; $T = {2, 3, ..., n}$.

Itérations

Tant que $T$ n'est pas vide faire

• Choisir $i$ dans $T$ tel que $l(i)$ est minimum
• Retirer $i$ de $T$ et l'ajouter à $S$
• Pour chaque successeur $j$ de $i$, avec $j$ dans $T$, faire Si $l(j) > l(i) + d(i,j)$ alors
  • $l(j) = l(i) + d(i,j)$
  • $p(j) = i$

Exemple

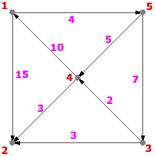
Initialisations

• $S = {1}$ ;
• $T = {2, 3, 4, 5}$ ;
• $l = (0, 15, \infty, \infty, 4)$;
• $p = (NIL, 1, NIL, NIL, 1)$.

Première itération

• $i = 5$ car $l(5) = min(15, \infty, \infty, 4) = 4$;
• $S = {1, 5}$; $T = {2, 3, 4}$;
• les successeurs de 5 dans $T$ sont 3 et 4;
• $l(3)$ prend la nouvelle valeur $min(\infty; l(5) + d(5; 3)) = min(\infty; 4 + 7) = 11$; $p(3) = 5$;
• $l(4)$ prend la nouvelle valeur $min(\infty ; l(5) + d(5; 4)) = 9$ ; $p(4) = 5$;
• d'où les nouveaux vecteurs $l = (0, 15, 11, 9, 4)$ et p = $(NIL, 1, 5, 5, 1)$

Deuxième itération

• $i = 4$; $l(4) = 9$;
• $S = {1, 5, 4}$; $T = {2, 3}$;
• le seul successeur de 4 dans $T$ est 2;
• $l(2)$ prend la nouvelle valeur $min(\infty; l(4) + d(4; 2)) = min(15; 9 + 3) = 12$; $p(2) = 4$;
• d'où les nouveaux vecteurs $l = (0, 12, 11, 9, 4)$ et $p = (NIL, 4, 5, 5, 1)$

Troisième itération

• $i = 3$; $l(3) = 11$;
• $S = {1, 5, 4, 3}$; $T = {2}$;
• le seul successeur de 3 dans $T$ est 2;
• $l(2)$ garde sa valeur car $min(12; l(3) + d(3; 2)) = min(12; 11 + 3) = 12$;
• d'où les vecteurs inchangés $l = (0, 12, 11, 9, 4)$ et $p = (NIL, 4, 5, 5, 1)$

Quatrième itération

• $i = 2$; $l(2) = 12$;
• $S = {1, 5, 4, 3, 2}$; $T={}$; FIN.
• $l = (0, 12, 11, 9, 4)$;
• $p = (NIL, 4, 5, 5, 1)$.

Le chemin minimal de 1 à 4 par exemple est de coût 9. C'est le chemin 1-5-4, car $p(4) = 5$ et $p(5) = 1$.

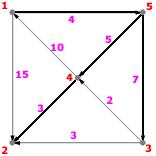
Exercices

---

Exercice : Appliquez l'algorithme de Dijkstra au graphe de l'exemple ci-dessus pour trouver tous les plus courts chemins en partant des sommets 2, 3, 4 et 5.

---

---

Exercice : Expliquez pourquoi des arcs avec des poids négatifs pourraient poser problème dans la recherche d'un plus court chemin dans un graphe.

---

Méthode PERT

Présentation de la méthode

Le problème du plus long chemin dans les digraphes sans circuits trouve une application dans l'ordonnancement et la planification des tâches composant un projet complexe, par exemple la construction d'une maison.

On fait correspondre à chaque tâche un arc d'un digraphe, sa durée d'exécution étant égale au poids de cet arc.

Le digraphe reflète les précédences requises dans l'exécution du projet. Ainsi, la tâche correspondant à l'arc $(i, j)$ ne peut commencer que si toutes les tâches correspondant à des arcs $(k, i)$ ont été complétées. Le digraphe peut contenir des tâches fictives de durée nulle afin de forcer certaines précédences.

Les sommets du digraphe représentent des événements, début (fin) des activités correspondant aux arcs dont ils sont l'extrémité initiale (finale). Le fait que le digraphe est sans circuit est garant de la faisabilité du projet. En effet, l'existence d'un circuit impliquerait une contradiction dans les précédences : une tâche devant en même temps précéder et succéder une autre!

On supposera dorénavant que les sommets ont déjà été numérotés de 1 à $n$ de manière compatible avec leurs rangs, c'est-à-dire que $r(j)>r(i)$ implique $j>i$ (voir l'algorithme de calcul du rang).

En plus, si le digraphe possède plusieurs sommets sans prédécesseurs, on supposera avoir introduit un sommet 1 relié par un arc de durée nulle à chacun de ces sommets. Ce sommet indique le début du projet.

De même, si le digraphe possède plusieurs sommets sans successeurs, ceux-ci seront reliés par un arc de durée nulle à un dernier sommet $n$ (fin du projet).

Enfin, on supposera éliminés les arcs parallèles par l'introduction de tâches fictives.

Algorithme du chemin critique

Données

Digraphe $G = (V, E)$, sans circuits, des activités avec leur durée $d_{ik}$.

Résultat

• $d_i$ début au plus tôt des activités correspondant aux arcs $(i, k)$ partant de $i$,
• $j_i$ fin au plus tard des activités correspondant aux arcs $(k, i)$ arrivant à $i$,
• durée du chemin critique.

Début

1. Calcul des dates de début au plus tôt (récurrence en avançant dans le projet)
2. $d_1 = 0$
3. Pour $k = 2$ à $n$ faire $d_k = max{d_j + d_{jk} | j \in P(k)}$
4. Calcul des dates de fin au plus tard (récurrence en reculant dans le projet)
5. $j_n = d_n$
6. Pour $k = n-1$ à 1 faire $j_k = min{j_j - d_{kj} | j \in S(k)}$

Fin.

Notation: $P(i) = {k \in V | (k, i) \in E}$ est l'ensemble des sommets prédécesseurs de $i$.

Notation: $S(i) = {k \in V | (i, k) \in E}$ est l'ensemble des sommets successeurs de $i$.

Définitions

---

Définition (Sommet critique)

Un sommet $i$ est critique si $d_i = j_i$.

---

---

Définition (Arc critique)

Un arc $(i, j)$ est critique si ses extrémités sont des sommets critiques et $d_{ij} = d_j - d_i$.

---

---

Définition (Chemin critique)

Un chemin critique est un chemin de 1 à $n$ n'utilisant que des arcs critiques, c'est-à-dire des activités telles que tout retard dans leur exécution provoquerait un retard de la fin du projet.

---

---

Définition (Durée du chemin critique)

La durée du chemin critique est donnée par $d_n$ (ou par $j_n$, les deux valeurs étant toujours égales). Elle correspond à la durée minimale du projet étant données les durées des tâches le composant et les précédences respectives.

---

Exemple

Ci-dessous le graphe des précédences obtenu avec l'algorithme du chemin critique. Les sommets et les arcs critiques sont en rouge.

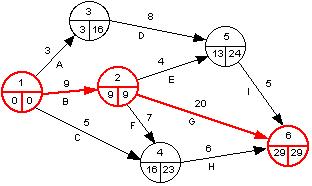
$Tâches $	$ Précédences $	$ Durée [jours] $
$A $	$ - $	$ 3 $
$B $	$ - $	$ 9 $
$C $	$ - $	$ 5$
$D $	$ A $	$ 8 $
$E $	$ B $	$ 4 $
$F $	$ B $	$ 7$
$G $	$ B $	$ 20$
$H $	$ C, F $	$ 6$
$I $	$ D, E $	$ 5$

Exercices

---

Exercice : Refaites le graphe des précédences de l'exemple en utilisant l'algorithme du chemin critique.

---

---

Exercice : La rénovation du séjour d'un appartement se décompose en plusieurs tâches décrites dans le tableau ci-dessous. Ce dernier donne également les précédences à respecter lors de la planification des travaux ainsi qu'une estimation de la durée de chacune des tâches.

$	Tâches	Précédences	Durée [jours]
$A $	Enlèvement des portes	$ - $	$ 1/2$
$B $	Ponçage et peinture des portes	$ A $	$ 3 $
$C $	Pose des portes	$ B, J $	$ 1/2 $
$D $	Arrachage des papiers peints	$ - $	$ 1$
$E $	Tirage des fils électriques	$ D $	$ 1 $
$F $	Pose des prises	$ E, H, I $	$ 1/2 $
$G $	Ragréage des murs	$ E, A $	$ 2$
$H $	Peinture du plafond	$ G $	$ 2$
$I $	Pose des papiers peints	$ G $	$ 3$
$J $	Peinture des cadres	$ H, I $	$ 1$
$K $	Arrachage de la moquette	$ H, I, J $	$ 1/2 $
$L $	Ponçage du parquet	$ K $	$ 1$
$M $	Imprégnation et séchage du parquet	$ L, F $	$ 4$
$N $	Peinture du balcon	$ - $	$ 2$
$O $	Changement des protections solaires	$ N $	$ 1$

1. Représentez le graphe des précédences de ces travaux de rénovation.
2. Déterminez une durée totale minimale de rénovation en exhibant un chemin critique dans le graphe précédent.

---