---

Définitions

Digraphe (graphe orienté), sommet, arc

En donnant un sens aux arêtes d'un graphe, on obtient un digraphe, ou graphe orienté.

Remarque : De l'anglais directed graph.

---

Définition (Digraphe, sommets, arcs)

Un digraphe fini $G = (V, E)$ est défini par :

• l'ensemble fini $V = {v_1, v_2, ..., v_n}$ ($|V| = n$) dont les éléments sont appelés sommets ,
• et par l'ensemble fini $E = {e_1, e_2, ..., e_m}$ ($|E| = m$) dont les éléments sont appelés arcs.

Un arc $e$ de l'ensemble $E$ est défini par une paire ordonnée de sommets. Lorsque $e = (u, v)$, on dira que l'arc $e$ va de $u$ à $v$. On dit aussi que $u$ est l'extrémité initiale et $v$ l'extrémité finale de $e$.

---

---

Exemple : Un exemple de digraphe :

---

---

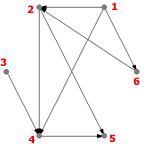
Exercice : Construire un graphe orienté dont les sommets sont les entiers compris entre 1 et 12 et dont les arcs représentent la relation « être diviseur de ».

---

---

Exercice : Quel est le nombre maximal d'arêtes dans un graphe orienté d'ordre $n$ qui ne possède pas d'arêtes parallèles ?

---

Exemples

1. Le graphe d'une relation binaire peut être assimilé à un graphe orienté,
2. Les graphes orientés peuvent être représentés graphiquement, ce qui fournit toutes sortes d'exemples :

Degré d'un sommet d'un digraphe

Soit $v$ un sommet d'un graphe orienté.

---

Définition (Degré extérieur)

Le degré extérieur du sommet $v$ est le nombre d'arcs ayant $v$ comme extrémité initiale.

---

Notation: On le note $d_+(v)$.

---

Définition (Degré intérieur)

Le degré intérieur du sommet $v$ est le nombre d'arcs ayant $v$ comme extrémité finale.

---

Notation: On le note $d_-(v)$.

---

---

Théorème

On a : $d(v) = d_+(v) + d_-(v)$.

---

---

---

Exercice : Soit $G$ un graphe orienté quelconque. Démontrez que la somme des degrés entrants de tous les sommets est égal à la somme de tous les degrés sortants.

---

Réponse : Chaque arête compte une fois dans la somme des degrés entrants et une fois dans la somme des degrés sortants... Exercice :

---

Exercice : Soit X un ensemble de lapins, et G un graphe orienté ayant X pour ensemble de sommets. On dit que G est un «graphe de parenté» si les arcs de G codent la relation «être l'enfant de...». Quelles conditions doit nécessairement vérifier G pour pouvoir être un graphe de parenté?

---

Chemins et circuits

Chemin

---

Définition (Chemin)

Un chemin conduisant du sommet $a$ au sommet $b$ est une suite de la forme ($v_0,e_1,v_1,e_2,v_2, ..., e_k,v_k$) où les $v_i$ sont des sommets ($v_0=a$ et $v_k=b$) et les $e_i$ sont des arcs tels que $e_i$ va de $v_{i-1}$ à $v_i$.

---

---

Exemple : Sur le digraphe ci-dessous, on peut voir par exemple le chemin ($v_3,e_3,v_4,e_4,v_5$).

---

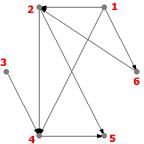
Remarque : Par convention, tout chemin comporte au moins un arc.

Distance

---

Définition (Distance)

On appelle distance entre deux sommets d'un digraphe la longueur du plus petit chemin les reliant.

S'il n'existe pas de chemin entre les sommets $x$ et $y$, on pose $d(x,y) = +\infty$.

---

---

Exemple : Par exemple, sur le digraphe ci-dessus (exemple précédent), $d(v_1,v_5)=2$, $d(v_1,v_6)=1$, $d(v_6,v_1)=+\infty$.

---

---

Exercice : Donnez un algorithme permettant de calculer la distance entre deux sommets x et y d'un digraphe connexe.

---

Circuit

---

Définition (Circuit)

Un circuit est un chemin avec $u_0=u_k$.

---

---

Exemple : Le digraphe ci-dessus ne contient pas de circuit.

---

Remarque : Les notions de longueur, de chemins et de circuits sont analogues à celles des chaînes et des cycles pour le cas non orienté.

Circuits eulériens

---

---

Théorème

Dans le cas des graphes orientés, il y a équivalence entre :

• posséder un circuit eulérien,
• être fortement connexe, tel que $d_+(s) = d_-(s)$ pour tout sommet $s$.

---

---

Digraphe fortement connexe

Définitions

Connexité forte

---

Définition (Digraphe fortement connexe)

Un digraphe est fortement connexe, si toute paire ordonnée ($a$, $b$) de sommets distincts du graphe est reliée par au moins un chemin.

---

Remarque : En d'autres termes, tout sommet est atteignable depuis tous les autres sommets par au moins un chemin.

---

Exercice : Les graphes ci-dessous sont-il fortement connexes? Si non, donnez leurs composantes fortement connexes.

---

Composantes connexes

---

Définition (Composante fortement connexe)

On appelle composante fortement connexe tout sous-graphe induit maximal fortement connexe (maximal signifie qu'il n'y a pas de sous-graphe induit connexe plus grand contenant les sommets de la composante).

---

Exercices

---

Exercice : On souhaite prélever 4 litres de liquide dans un tonneau. Pour cela, nous avons à notre disposition deux récipients (non gradués!), l'un de 5 litres, l'autre de 3 litres.

Comment doit-on procéder?

---

---

Exercice : Donnez un algorithme permettant de calculer la distance entre deux sommets x et y d'un digraphe connexe.

---

---

Exercice : Proposez un algorithme qui détermine si un graphe est fortement connexe ou non.

---

Indication : utilisez un système de marquage des sommets.

---

Exercice : Les graphes ci-dessous sont-il fortement connexes? Si non, donnez leurs composantes fortement connexes.

---

Matrice et listes d'adjacences

Matrice d'incidence

---

Définition (Matrice d'incidence entrante et sortante)

On suppose que les arêtes et les sommets ont été numérotés.

On appelle matrice d'incidence sortante $J^+$ la matrice dont l'élément $J^+(s,\varepsilon)$ vaut

• 1 si le sommet $d$ est le début de l'arête ${\varepsilon}$,
• 0 sinon.

On appelle de même matrice d'incidence entrante $J^-$ la matrice dont l'élément $(s,\varepsilon )$ vaut :

• 1 si le sommet $s$ est la fin de l'arête $\varepsilon$,
• 0 sinon.

---

\begin{Def} On suppose à nouveau que les arêtes et les sommets du graphe orienté considéré ont été numérotées, et on appelle alors matrice d'incidence J de ce graphe la matrice dont l'élément $(s,\varepsilon)$ vaut :

• 2 si $s$ est une extrémité de $\varepsilon$, quand $\varepsilon$ est une boucle,
• 1 si $s$ est une extrémité de $\varepsilon$, quand $\varepsilon$ n'est pas une boucle,
• 0 sinon.

---

Remarques

1. se donner un graphe orienté est équivalent à se donner les deux matrices $J^+$ et $J^-$.
2. on peut relier $d^+(s)$ (resp. $d^-(s)$) au nombre de 1 apparaissant dans $J^+$ (resp. $J^-$).

Résultats

---

---

Théorème

Soient $(s_1, , s_n)$ les sommets d'un graphe orienté. Alors

1. $\left( \begin{array}{c} d^+(s_1) \\ \vdots \\ d^+(s_n) \\ \end{array} \right) = J^+ \left( \begin{array}{c} 1 \\ \vdots \\ 1 \\ \end{array} \right)

$

1. $\left( \begin{array}{c} d^-(s_1) \\ \vdots \\ d^-(s_n) \\ \end{array} \right) = J^- \left( \begin{array}{c} 1 \\ \vdots \\ 1 \\ \end{array} \right)$
2. $J^{+}J^{-t} = \left( \begin{array}{ccc} d^+(s_1) & & 0 \\ & \ddots & \\ 0 & & d^+(s_n) \end{array} \right)$
3. $J^{-}J^{+t} = \left( \begin{array}{ccc} d^-(s_1) & & 0 \\ & \ddots & \\ 0 & & d^-(s_n) \end{array} \right)$

---

---

Matrice d'adjacences

Définition

---

Définition (Matrice d'adjacences)

On peut représenter un digraphe par une matrice d'adjacences :

• Les lignes et les colonnes représentent les sommets du graphe.
• Un 1 à la position ($i$,$j$) signifie qu'un arc part de $i$ pour rejoindre $j$.

---

Exemple

Voici la matrice d'adjacences du digraphe G:

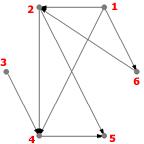
$M = \left(\begin{array}{cccccc}0 & 1 & 0 & 1 & 0 & 1 \\0 & 0 & 0 & 1 & 1 & 0 \\0 & 0 & 0 & 1 & 0 & 0 \\0 & 0 & 0 & 0 & 1 & 0 \\0 & 0 & 0 & 0 & 0 & 0 \\0 & 1 & 0 & 0 & 0 & 0 \\\end{array}\right)$

---

Exercice : Décrivez le digraphe G ci-contre par une matrice d'adjacences.

---

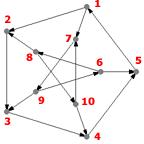
Remarque : Se donner un graphe orienté revient à se donner sa matrice d'adjacence.

Propriétés

---

---

Théorème

La matrice d'adjacence à plusieurs caractéristiques :

• Elle est carrée : il y a autant de lignes que de colonnes.
• Il n'y a que des zéros sur la diagonale. Un 1 sur la diagonale indiquerait une boucle.
• Contrairement au cas non orienté, elle n'est pas symétrique.

---

---

---

---

Théorème (Nombre de chemins de longueur k)

$A^k(s,t)$, élément à la position $(s,t)$ de la puissance k^ième de A, est aussi le nombre de chemins de longueur k qui mènent de $s$ à $t$.

---

---

---

---

Théorème (Lien entre les matrices d'adjacence)

Soit A la matrice d'adjacence d'un graphe orienté, et B la matrice d'adjacence du graphe non orienté qui lui est associé. Alors $B = A+A^t$

---

---

Lien entre matrices d'adjacences et d'incidences

Les remarques précedentes permettent de conclure que se donner ($J^+,J^-$) ou $A$, « c'est pareil ». Plus précisément, on a $J^{+}J^{-t} = A$

---

Exercice : On pose $A=\left( \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{array}\right)$

1. Dessinez le graphe orienté ayant $A$ pour matrice d'adjacence.
2. Déterminez ses matrices d'incidences.
3. Vérifiez, sur cet exemple, les formules précédentes.

---

---

Exercice : A partir du graphe orienté $G$, on fabrique un graphe orienté $H$ en retournant le sens de toutes les flèches.

1. Comment sont liées les matrices d'incidence de $G$ et de $H$ ?
2. Comment sont liées leurs matrices d'adjacence ?

---

Réponse : La matrice $J^+$ de $G$ est la matrice $J^-$ de $H$, et réciproquement. Leurs matrices d'adjacence sont transposées l'une de l'autre.

---

---

Théorème

Soient $s_1, s_2, , s_n$ les sommets d'un graphe orienté. Alors $\left( \begin{array}{c} d(s_1) \\ \vdots \\ d(s_n) \end{array} \right) = J \left( \begin{array}{c}1 \\\vdots \\1 \\\end{array} \right)$

---

---

---

---

Théorème (relation entre $J, J^+$ et $J^-$)

On note $J^+$ et $J^-$ les matrices d'incidences d'un graphe orienté, et J la matrice d'incidence du graphe non orienté qui lui est associé. Alors $J = J^+ + J^-$

---

---

Listes d'adjacence

On peut encore représenter un digraphe à l'aide de listes d'adjacences : en donnant pour chacun de ses sommets la liste des sommets qu'on peut atteindre directement en suivant un arc (dans le sens de la flèche).

---

Exemple : Voici les listes d'adjacences du digraphe G:

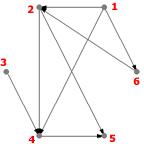
$1 $	$ : $	$ 2, 4, 6$
$2 $	$ : $	$ 4, 5$
$3 $	$ : $	$ 4$
$4 $	$ : $	$ 5$
$5 $	$ : $	$ -$
$6 $	$ : $	$ 2$

---

---

---

Théorème

Soient $(s_1, , s_n)$ les sommets d'un graphe orienté. Alors $\left( \begin{array}{c} d^+(s_1)\\ \vdots \\ d^+(s_n) \end{array} \right) = A \left(\begin{array}{c}1 \\\vdots \\1 \\\end{array} \right) \textrm{ et } \left( \begin{array}{c} d^-(s_1)\\ \vdots \\ d^-(s_n) \end{array} \right) = A^t \left( \begin{array}{c}1 \\\vdots \\1 \\\end{array} \right) $

---

---

---

Exercice : Décrivez le digraphe $G$ de l'exercice précédent par des listes d'adjacences.

---

Digraphes sans circuits

Théorème

---

---

Théorème

Le digraphe $G = (V, E)$ est sans circuits si et seulement si on peut attribuer un nombre $r(v)$, appelé le rang de $v$, à chaque sommet $v$ de manière que pour tout arc $(u, v)$ de $G$ on ait $r(u) < r(v)$.

---

---

Preuve : Si $G$ comporte un circuit $C$, il n'est pas possible de trouver de tels nombres $r(i)$ car, autrement, considérant $r(j) = max {r(i) | i \in C}$ et l'arc $(j, k) \in C$ on aurait $r(j) \leqslant r(k)$ en contradiction avec la définition de $r( )$.

Réciproquement, si $G$ n'a pas de circuits, il existe au moins un sommet sans prédécesseurs dans $G$ (sans cela, en remontant successivement d'un sommet à un prédécesseur, on finirait par fermer un circuit). Ainsi, on peut attribuer séquentiellement des valeurs $r( )$ aux sommets du graphe à l'aide de l'algorithme qui suit, ce qui conclura la démonstration.

Algorithme de calcul du rang

Donnée

digraphe $G = (V, E)$ sans circuit.

Résultat

rang $r(v)$ de chaque sommet $v \in V$ du digraphe $G$.

Début

• $r = 0$, $X = V$
• $R$ l'ensemble des sommets de $X$ sans prédécesseurs dans $X$
• Tant que $X$ n'est pas vide faire
• $r(v) = r$ pour tout sommet $v \in R$
• $X = X - R$
• $R$ l'ensemble des sommets de $X$ sans prédécesseurs dans $X$
• $r = r + 1$

Fin

Exercice

---

Exercice : Attribuez un rang aux sommets du digraphe ci-dessous en utilisant l'algorithme de calcul du rang :

---