---

Définition

---

Définition (Arbre couvrant)

Un arbre couvrant (ou arbre maximal) est un graphe partiel qui est aussi un arbre.

---

Remarque : On rappelle qu'un graphe partiel de G est obtenu en enlevant des arêtes (mais pas de sommets) à G.

---

Exemple : Un des arbres couvrants (en bleu) d'un graphe donné.

---

---

Exercice : Combien d'arbres couvrants différents les graphes suivants possèdent-ils ?

---

---

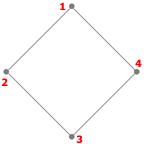
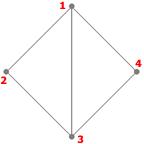
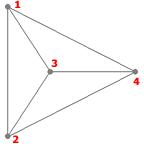
Exercice : Trouvez un arbre couvrant minimal pour chaque graphe ci-dessus.

---

Arbre maximal de poids minimum

Présentation du problème

On considérera le problème suivant :

« Soit le graphe $G = (V, E)$ avec un poids associé à chacune de ses arêtes. Trouver, dans $G$, un arbre maximal $A = (V, F)$ de poids total minimum.»

Ce problème se pose, par exemple, lorsqu'on désire relier $n$ villes par un réseau routier de coût minimum. Les sommets du graphe représentent les villes, les arêtes, les tronçons qu'il est possible de construire et les poids des arêtes correspondent aux coûts de construction du tronçon correspondant.

L'algorithme de Kruskal décrit ci-dessous permet de résoudre ce problème.

L'algorithme de Kruskal

Voici un algorithme célèbre permettant de résoudre ce problème :

---

---

Théorème (L'algorithme de Kruskal)

Pour obtenir un arbre ou une forêt couvrant(e) de poids minimum à partir d'un graphe pondéré $G = (S,A)$, on procède comme suit :

1. On part du graphe $G' = (S, ∅)$ ($G$ sans arête).
2. Tant que le nombre d'arêtes de $G'$ est inférieur à $min(|G|-1,|A|)$, faire
   1. Prendre la plus petite arête (de poids minimal) restante dans $G$.
   2. L'ajouter à $G'$ si cela ne crée pas de cycle.
   3. La supprimer de $G$.

---

---

Travaux pratiques

1. Programmer l'algorithme de Kruskal.
2. L'utiliser pour résoudre les exercices ci-dessous.
3. Trouver des arbres de poids minimum de http://www.math.u-psud.fr/~montcouq/Enseignements/Apprentis/feuille5.pdf
4. Résoudre le pb énoncé au transparent 111 de http://www.math.u-psud.fr/~montcouq/Enseignements/Apprentis/arbres.pdf

---

Exercice : Le tableau suivant donne les coûts de construction de routes (exprimées en unités adéquates) entre six villes d'Irlande.

	Athlone	Dublin	Galway	Limerick	Sligo	Wexford
Athlone	-	78	56	73	71	114
Dublin	-	-	132	121	135	96
Galway	-	-	-	64	85	154
Limerick	-	-	-	-	144	116
Sligo	-	-	-	-	-	185

Trouver une manière de relier ces six villes, en minimisant le coût total de construction.

---

---

Exercice : Faire de même avec le tableau suivant, qui comptabilise cette fois-ci les kilomètres entre chaque ville (valeurs imaginaires) :

	Athlone	Dublin	Galway	Limerick	Sligo	Wexford
Athlone	-	121	95	43	71	74
Dublin	-	-	72	98	115	97
Galway	-	-	-	64	77	134
Limerick	-	-	-	-	144	126
Sligo	-	-	-	-	-	85

---