WikiMath
This is Wordpress NewsPaper Theme converted to PmWiki
Arbres
Présentation générale
Définitions
Définition (Arbre, feuilles)
On nomme arbre un graphe non orienté connexe et acyclique (sa forme évoque en effet la ramification des branches d'un arbre). On distingue deux types de sommets dans un arbre
- les feuilles dont le degré est 1;
- les nœuds internes dont le degré est supérieur à 1.
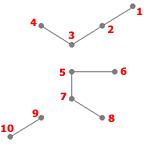
Exemple : Un exemple d'arbre :

Définition (Forêt)
Un graphe sans cycles mais non connexe est appelé une forêt.
Exemple : Un exemple de forêt :
Caractérisation des arbres
Théorème
Les affirmations suivantes sont équivalentes pour tout graphe $G = (V, E)$ à $n$ sommets.
- $G$ est un arbre,
- $G$ est sans cycles et connexe,
- $G$ est sans cycles et comporte $n-1$ arêtes,
- $G$ est connexe et comporte $n-1$ arêtes,
- Chaque paire $(u, v)$ de sommets distincts est reliée par une seule chaîne simple (et le graphe est sans boucles).
Nombre minimal de feuilles
Théorème
Tout arbre fini avec au moins deux sommets comporte au moins deux feuilles.
Travaux pratiques
- Utiliser networkx et un résultat ci-dessus pour écrire une fonction qui teste si un graphe donné est un arbre. On pourra penser à une méthode networkx qui teste si un graphe est connexe, à savoir is_connected(G), puis comparer les nombres de sommets G.nodes() et d'arêtes G.edges()...
- Idem, mais pour une forêt.
Codage de Prüfer
Présentation
Le codage de Prüfer est une manière très compacte de décrire un arbre.
Codage
La méthode
Soit l'arbre $T = (V, E)$ et supposons $V = {1, 2, ..., n}$. L'algorithme ci-dessous fournira le code de $T$, c'est-à-dire une suite $S$ de $n-2$ termes employant (éventuellement plusieurs fois) des nombres choisis parmi ${1, ..., n}$.
Théorème (Pas général de l'algorithme de codage)
Initialement la suite $S$ est vide. Ce pas général est à répéter tant qu'il reste plus de deux sommets dans l'arbre courant $T$ :
- identifier la feuille $v$ de l'arbre courant ayant le numéro minimum ;
- ajouter à la suite $S$ le seul sommet $s$ adjacent à $v$ dans l'arbre $T$ courant ;
- enlever de l'arbre $T$ courant la feuille $v$ et l'arête incidente à $v$.
Exemple de codage
- Étape 0
- Arbre à coder:
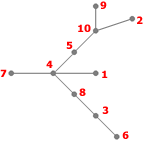
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1, 5, 7, 8
- 5: 4, 10
- 6: 3
- 7: 4
- 8: 3, 4
- 9: 10
- 10: 2, 5, 9
- Étape 1
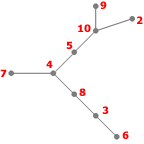
Listes des sommets adjacents :
- 2: 10
- 3: 6, 8
- 4: 5, 7, 8
- 5: 4, 10
- 6: 3
- 7: 4
- 8: 3, 4
- 9: 10
- 10: 2, 5, 9
S={4}
- Étape 2

Listes des sommets adjacents :
- 3: 6, 8
- 4: 5, 7, 8
- 5: 4, 10
- 6: 3
- 7: 4
- 8: 3, 4
- 9: 10
- 10: 5, 9
S={4,10}
- Étape 3
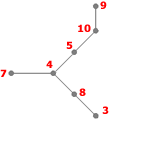
Listes des sommets adjacents :
- 3: 8
- 4: 5, 7, 8
- 5: 4, 10
- 7: 4
- 8: 3, 4
- 9: 10
- 10: 5, 9
S={4,10,3}
- Étape 4

Listes des sommets adjacents :
- 4: 5, 7, 8
- 5: 4, 10
- 7: 4
- 8: 4
- 9: 10
- 10: 5, 9
S = {4,10,3,8}
- Étape 5

Listes des sommets adjacents :
- 4: 5, 8
- 5: 4, 10
- 8: 4
- 9: 10
- 10: 5, 9
S = {4,10,3,8,4}
- Étape 6
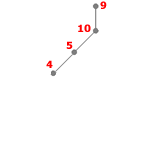
Listes des sommets adjacents :
- 4: 5
- 5: 4, 10
- 9: 10
- 10: 5, 9
S = {4,10,3,8,4,4}
- Étape 7
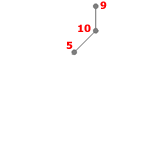
Listes des sommets adjacents :
- 5: 10
- 9: 10
- 10: 5, 9
S = {4,10,3,8,4,4,5}
- Étape 8
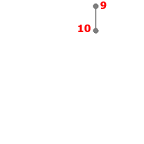
Listes des sommets adjacents :
- 9: 10
- 10: 9
S = {4,10,3,8,4,4,5,10}
- Étape 9
- S = {4,10,3,8,4,4,5,10} est le codage de Prüfer de l'arbre initial.
Décodage
La méthode
- Donnée
- suite $S$ de $n-2$ nombres, chacun provenant de {1, ..., n}.
Posons $I = {1, ..., n}$.
- Pas général de l'algorithme de décodage
à répéter tant qu'il reste des éléments dans $S$ et plus de deux éléments dans $I$
- identifier le plus petit élément $i$ de $I$ n'apparaissant pas dans la suite $S$ ;
- relier par une arête de $T$ le sommet $i$ avec le sommet $s$ correspondant au premier élément de la suite $S$ ;
- enlever $i$ de $I$ et $s$ de $S$.
- Finalisation
- Les deux éléments qui restent dans I à la fin de l'algorithme constituent les extrémités de la dernière arête à ajouter à T.
Exemple de décodage
- Étape 0
- arbre à décoder

I={1,2,3,4,5,6,7,8,9,10}, S={4,10,3,8,4,4,5,10}
- Étape 1

Listes des sommets adjacents :
- 1: 4
- 4: 1
I={2,3,4,5,6,7,8,9,10}, S={10,3,8,4,4,5,10}
- Étape 2
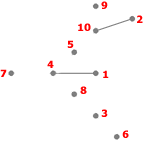
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 4: 1
- 10: 2
I={3,4,5,6,7,8,9,10}, S={3,8,4,4,5,10}
- Étape 3
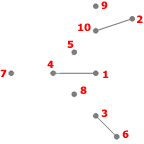
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6
- 4: 1
- 6: 3
- 10: 2
I={3,4,5,7,8,9,10}, S={8,4,4,5,10}
- Étape 4
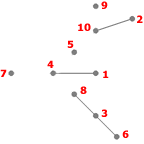
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1
- 6: 3
- 8: 3
- 10: 2
I={4,5,7,8,9,10}, S={4,4,5,10}
- Étape 5
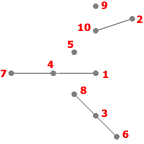
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1, 7
- 6: 3
- 7: 4
- 8: 3
- 10: 2
I={4,5,8,9,10}, S={4,5,10}
- Étape 6

Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1, 7, 8
- 6: 3
- 7: 4
- 8: 3, 4
- 10: 2
I={4,5,9,10}, S={5,10}
- Étape 7

Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1, 5, 7, 8
- 5: 4
- 6: 3
- 7: 4
- 8: 3, 4
- 10: 2
I={5,9,10}, S={10}
- Étape 8
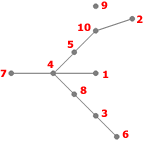
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1, 5, 7, 8
- 5: 4, 10
- 6: 3
- 7: 4
- 8: 3, 4
- 10: 2, 5
I={9,10}
S={}
- Étape 9
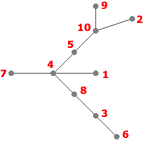
Listes des sommets adjacents :
- 1: 4
- 2: 10
- 3: 6, 8
- 4: 1, 5, 7, 8
- 5: 4, 10
- 6: 3
- 7: 4
- 8: 3, 4
- 9: 10
- 10: 2, 5, 9
I={}, S={}
Théorème de Cayley
Théorème (Cayley, 1857)
Le nombre d'arbres que l'on peut construire sur $n$ ($n>1$) sommets numérotés est égal à $n^{n-2}$.
Preuve : La preuve est immédiate en utilisant le codage de Prüfer.
En effet, on vérifie aisément que les deux algorithmes constituent les deux sens d'une bijection entre les arbres sur n sommets numérotés et les mots de $n-2$ lettres sur l'alphabet à $n$ lettres.
Ce constat permet de conclure la preuve du théorème de Cayley. En effet, il existe $n^{n-2}$ mots de longueur $n-2$ sur l'alphabet à $n$ lettres, donc d'arbres sur $n$ sommets numérotés.
Travaux pratiques
- Faire une fonction de codage et une fonction de décodage d'un arbre par la méthode de Prüfer. On pourra utiliser les éléments suivants :
- G.nodes() produit la liste des sommets de G
- G.degree(k) donne le degré du sommet k (son nombre d'arêtes)
- G.neighbors(k) donne la liste des sommets adjacents au sommet k
- G.remove_node(k) supprime le sommet k
- min(L) renvoie le plus petit élément de L
- L.remove(x) supprime l'élément x dans la liste L
- del L[0] supprime le premier élément de la liste L
- Décrivez l'arbre ci-dessous à l'aide du codage de Prüfer.

- Dessinez l'arbre correspondant à la suite S={1,1,1,1,1,1,1,1,1}.