---

Principe

Le codage de Huffman (1952) est un algorithme de compression sans perte, utilisant la notion d'arbres, qui permet de réduire la taille de données numériques.

Le principe, élémentaire, consiste à choisir de ne plus coder chaque symbole avec un nombre fixe de bits, mais à coder les symboles les plus fréquents avec un plus petit nombre de bits (quitte à devoir utiliser beaucoup de bits pour les symboles les plus rares).

---

Exemple : Par exemple, dans un texte donné, le $w$ apparait 20 fois moins souvent que le $e$. Plutôt que de coder chaque lettre sur un octet, on va donc :

• Coder le $e$ par 1 (un seul bit, au lieu de 8),
• Coder le $w$ par 010100000100 (12 bits, au lieu de 8).

Si le $w$ apparaît 10 fois (donc le $e$ 200 fois), le gain sera de $7 \times 200 - 4 \times 10 = 1360$ bits, rien qu'en considérant ces deux lettres.

---

Cet algorithme offre des taux de compression démontrés les meilleurs possibles pour un codage par symbole, et il est assez compliqué de mieux compresser.

Propriété de préfixe

Le codage ne peut pas se faire n'importe comment : il faut pouvoir décoder, sans ambiguïté.

---

Exemple : Si l'on décide de :

• Coder le $e$ par 0,
• Coder le $w$ par 010100000100,
• Coder le $x$ par 10100000100,

Alors le texte 010100000100 pourra se traduire à la fois par $ex$, et $w$. On ne peut pas accepter une telle indétermination.

---

Le codage de Huffman a donc une propriété de préfixe : une séquence binaire ne peut jamais être à la fois représentative d'un élément codé et constituer le début du code d'un autre élément.

---

Exemple : Si un symbole est représenté par la combinaison binaire 100, alors la combinaison 10001 ne peut être le code d'aucune autre information.

---

Cette caractéristique du codage de Huffman permet une codification à l'aide d'une structure d'arbre binaire...

Méthode

L'algorithme opère sur une forêt. Une forêt est ici un ensemble d'arbres étiquetés complets : tout noeud interne (c'est-à-dire qui n'est pas une feuille) a deux fils non-vides.

La forêt initiale

est formée d'un arbre à un nœud pour chaque lettre du langage-source, dont l'étiquette est la probabilité de cette lettre.

La forêt finale

est formée d'un unique arbre, qui est l'arbre de décodage du code.

L'algorithme

est de type glouton il choisit à chaque étape les deux arbres d'étiquettes minimales, soit x et y, et les remplace par l'arbre formé de x et y et ayant comme étiquette la somme de l'étiquette de x et de l'étiquette de y.

Voici les différentes étapes de la construction d'un code de Huffman pour l'alphabet source {A, B, C, D, E, F}, avec les probabilités P(A)=0.10, P(B)=0.10, P(C)=0.25, P(D)=0.15, P(E)=0.35 et P(F)=0.05.

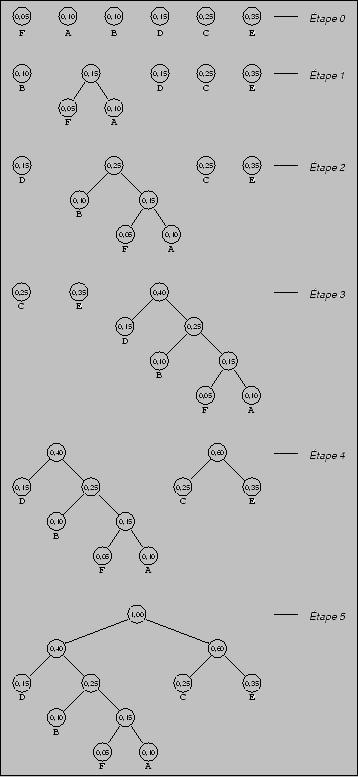
Le code d'une lettre est alors déterminé en suivant le chemin depuis la racine de l'arbre jusqu'à la feuille associée à cette lettre en concaténant successivement un 0 ou un 1 selon que la branche suivie est à gauche ou à droite.

---

Exemple : Ainsi, sur la figure ci-contre, A=0111, B=010, C=10, D=00, E=11 et F=0110.

---

---

Exemple : Par exemple le mot FADE serait codé 011001110011. Pour décoder, on lit simplement la chaîne de bits de gauche à droite. Le seul "découpage" possible, grâce à la propriété du préfixe, est 0110-0111-00-11.

---

Applications

Malgré son ancienneté, le codage de Huffman est toujours au goût du jour, et offre encore des performances appréciables. Il est utilisé dans presque toutes les applications qui impliquent la compression et la transmission de données numériques : fax, modems, réseaux informatiques, télévision HD, etc.

Les premiers Macintosh utilisaient un code inspiré de Huffman pour la représentation des textes : chaque lettre faisait tantôt 4 bits, tantôt 12 bits, suivant sa fréquence d'apparition dans le texte. Cette méthode simple se révélait économiser 30Le MPEG-1/2 Audio Layer 3, plus connu sous son abréviation de MP3, est constitué de deux étapes de compression :

• La première, avec perte, revient à la mise à l'écart de données inaudibles pour l'oreille humaine.
• La deuxième est un codage de Huffman.

Le logiciel de compression gzip (GNU zip) utilise Huffman (avec un autre algorithme : LZ77). Sa version améliorée, l'algorithme bzip2, utilise la transformée de Burrows-Wheeler avec le codage de Huffman.

Ce principe de compression est aussi utilisé dans le codage d'images. Il fait par exemple partie des spécifications des formats :

• TIFF (Tagged Image Format File) spécifié par Microsoft Corporation et Aldus Corporation. Le codage d'image est fait en retranscrivant exactement le contenu d'un écran (image), en utilisant Huffman.
• JPG (Join Photographic Experts Group), algorithme de compression avec perte, dont un des éléments est Huffman.

Travaux pratiques

1. Programmer le codage de Huffman.
2. Programmer le décodage.
3. Prendre un texte du projet Gutenberg et le compresser.